Evoluation d’une population (correction)#
Links: notebook, html, PDF, python, slides, GitHub
Evolution d’une population à partir des tables de mortalités et d’une situation initiale.
%matplotlib inline
import matplotlib.pyplot as plt
from jyquickhelper import add_notebook_menu
add_notebook_menu()
Exercice 1 : pyramides des âges#
from actuariat_python.data import population_france_year
population = population_france_year()
df = population
df.head(n=3)
| naissance | age | hommes | femmes | ensemble | |
|---|---|---|---|---|---|
| 0 | 2019 | 0 | 360058 | 346324 | 706382 |
| 1 | 2018 | 1 | 365656 | 350503 | 716159 |
| 2 | 2017 | 2 | 371835 | 357304 | 729139 |
hommes = df["hommes"]
femmes = df["femmes"]
somme = hommes - femmes
Je reprends ici le code exposé à Damien Vergnaud’s Homepage en l’adaptant un peu avec les fonctions de matplotlib via l’interface pyplot. Puis j’ajoute la différence par âge. On commence souvent par la gallerie pour voir si un graphe ou juste une partie est similaire à ce qu’on veut obtenir.
from matplotlib import pyplot as plt
from numpy import arange
fig, ax = plt.subplots(figsize=(8,8))
ValH = ax.barh(arange(len(hommes)), hommes, 1.0, label="Hommes",
color='b', linewidth=0, align='center')
ValF = ax.barh(arange(len(femmes)), -femmes, 1.0, label="Femmes",
color='r', linewidth=0, align='center')
diff, = ax.plot(somme, arange(len(femmes)), 'y', linewidth=2)
ax.set_title("Pyramide des âges")
ax.set_ylabel("Ages")
ax.set_xlabel("Habitants")
ax.set_ylim([0, 110])
ax.legend((ValH[0], ValF[0], diff), ('Hommes', 'Femmes', 'différence'));
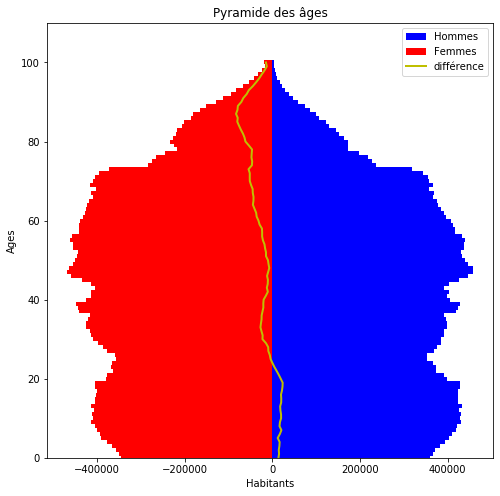
Le même en utilisant la fonction insérée dans le module actuariat_python.
from actuariat_python.plots import plot_population_pyramid
plot_population_pyramid(df["hommes"], df["femmes"], figsize=(8, 4));

Exercice 2 : calcul de l’espérance de vie#
Le premier objectif est de calculer l’espérance de
vie à l’âge
à partir de la table de mortalité. On récupère cette table.
from actuariat_python.data import table_mortalite_france_00_02
df=table_mortalite_france_00_02()
import pandas
pandas.concat([df.head(n=3), df.tail(n=3)])
| Age | Homme | Femme | |
|---|---|---|---|
| 0 | 0 | 100000.0 | 100000.0 |
| 1 | 1 | 99511.0 | 99616.0 |
| 2 | 2 | 99473.0 | 99583.0 |
| 115 | 117 | 0.0 | 0.0 |
| 116 | 118 | 0.0 | 0.0 |
| 117 | 120 | 0.0 | 0.0 |
On note la population l’âge
. La probabilité de
mourir à la date
lorsqu’on a l’âge
correspond à la
probabilité de rester en vie à jusqu’à l’âge
puis de mourir
dans l’année qui suit :
.
L’espérance de vie s’exprime :
On crée une matrice allant de 0 à 120 ans et on pose
. On utilise le module
numpy.
import numpy
hf = df[["Homme", "Femme"]].values
hf = numpy.vstack([hf, numpy.zeros((8, 2))])
hf.shape
(126, 2)
nb = hf.shape[0]
esp = numpy.zeros ((nb,2))
for t in range(0,nb):
for i in (0,1):
if hf[t,i] == 0:
esp[t,i] = 0
else:
somme = 0.0
for d in range(1,nb-t):
if hf[t+d,i] > 0:
somme += d * (hf[t+d,i] - hf[t+d+1,i]) / hf[t,i]
esp[t,i] = somme
esp[:1]
array([[75.00752, 82.48832]])
Enfin, on dessine le résultat avec matplotlib :
h = plt.plot(esp)
plt.legend(h, ["Homme", "Femme"])
plt.title("Espérance de vie");
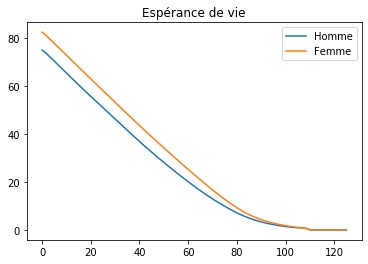
Le calcul implémenté ci-dessus n’est pas le plus efficace. On fait deux
boucles imbriquées dont le coût global est en mais
surtout on effectue les mêmes calculs plusieurs fois. Pour le réduire à
un coût linéaire
, il faut s’intéresser à la quantité :
L’implémentation devra utiliser la fonction numpy.cumsum et cette astuce Pandas Dataframe cumsum by row in reverse column order?.
# à suivre
numpy et pandas ont plusieurs fonction en commun dès qu’il s’agit de parcourir les données. Il existe aussi la fonction DataFrame.cumsum.
Exercice 3 : simulation de la pyramide l’année suivante#
L’objectif est d’estimer la population française à l’année . Si
désigne le nombre de personnes d’âge
en
, on peut estimer
en utilisant la probabilité
de mourir
:
On commence par calculer les coefficients avec la table
hf obtenue lors de l’exercice précédent tout en gardant la même
dimension (on aura besoin de la fonction
nan_to_num
:
mortalite = (hf[:-1] - hf[1:]) / hf[:-1]
mortalite = numpy.nan_to_num(mortalite) # les divisions nulles deviennent nan, on les remplace par 0
mortalite = numpy.vstack([mortalite, numpy.zeros((1, 2))])
m = mortalite
c:python372_x64libsite-packagesipykernel_launcher.py:1: RuntimeWarning: invalid value encountered in true_divide """Entry point for launching an IPython kernel.
La population a été obtenue lors de l’exercice 1, on la convertit en un objet numpy :
pop = population[["hommes","femmes"]].values
pop = numpy.vstack( [pop, numpy.zeros((m.shape[0] - pop.shape[0], 2))])
pop0 = pop.copy()
pop.shape
(126, 2)
Ensuite on calcule la population en 2020 :
pop_next = pop * (1-m)
pop_next = numpy.vstack([numpy.zeros((1, 2)), pop_next[:-1]])
pop_next[:5]
array([[ 0. , 0. ],
[358297.31638 , 344994.11584 ],
[365516.36791912, 350386.88814046],
[371734.07266293, 357228.65195867],
[382450.37346902, 366544.40263353]])
pop[:5]
array([[360058., 346324.],
[365656., 350503.],
[371835., 357304.],
[382535., 366607.],
[393693., 377204.]])
from actuariat_python.plots import plot_population_pyramid
plot_population_pyramid(pop_next[:, 0], pop_next[:, 1]);
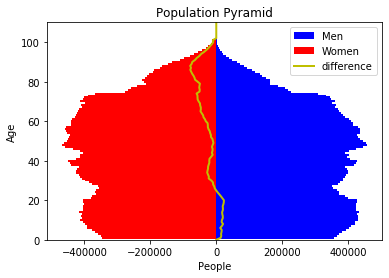
Exercice 4 : simulation jusqu’en 2100#
Il s’agit de répéter l’itération effectuée lors de l’exercice précédent. Le plus est de recopier le code dans une fonction et de l’appeler un grand nombre de fois.
def iteration(pop, mortalite):
pop_next = pop * (1-mortalite)
pop_next = numpy.vstack([numpy.zeros((1, 2)),
pop_next[:-1]]) # aucune naissance
return pop_next
popt = pop
for year in range(2020, 2051):
popt = iteration(popt, mortalite)
plot_population_pyramid(popt[:,0], popt[:,1], title="Pyramide des âges en 2050");
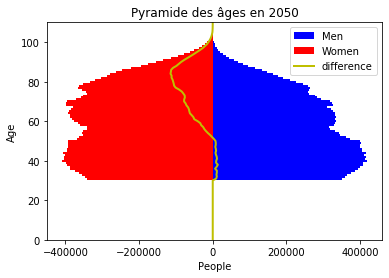
Exercice 5 : simulation avec les naissances#
Dans l’exercice précédent, la seconde ligne de la fonction iteration correspond à cas où il n’y a pas de naissance. On veut remplacer cette ligne par quelque chose proche de la réalité :
les naissances sont calculées à partir de la population féminines et de la table de fécondité
on garde la même proportion homme/femme que celle actuellement observée
ratio = pop[0, 0] / (pop[0, 1] + pop[0, 0])
ratio
0.5097213688910532
Il y a un peu plus de garçons qui naissent chaque année.
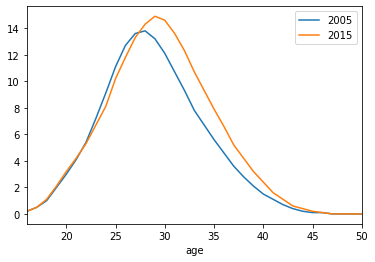
from actuariat_python.data import fecondite_france
df = fecondite_france()
df.head()
| age | 2005 | 2015 | |
|---|---|---|---|
| 4 | 16.0 | 0.2 | 0.2 |
| 5 | 17.0 | 0.5 | 0.5 |
| 6 | 18.0 | 1.0 | 1.1 |
| 7 | 19.0 | 2.0 | 2.1 |
| 8 | 20.0 | 3.0 | 3.2 |
from matplotlib import pyplot as plt
df.plot(x="age", y=["2005", "2015"]);
On convertit ces données en une matrice numpy sur 120 lignes comme les précédentes. On se sert des méthodes fillna et merge.
ages = pandas.DataFrame(dict(age=range(0,120)))
merge = ages.merge(df, left_on="age", right_on="age", how="outer")
fecondite = merge.fillna(0.0)
fecondite[13:17]
| age | 2005 | 2015 | |
|---|---|---|---|
| 13 | 13 | 0.0 | 0.0 |
| 14 | 14 | 0.0 | 0.0 |
| 15 | 15 | 0.0 | 0.0 |
| 16 | 16 | 0.2 | 0.2 |
mat_fec = fecondite[["2015"]].values / 100 # les chiffres sont pour 100 femmes
mat_fec.shape
(120, 1)
mat_fec.sum()
1.899
Si la matrice pop a plus de ligne que la matrice mat_fec, on
doit compléter la seconde avec autant de lignes nulles que la
précédente.
if mat_fec.shape[0] < pop.shape[0]:
zeros = numpy.zeros((pop.shape[0] - mat_fec.shape[0], mat_fec.shape[1]))
mat_fec = numpy.vstack([mat_fec, zeros])
mat_fec.sum()
1.899
Il faut maintenant coder une fonction qui calcule le naissances pour l’année suivantes.
def naissances(pop, fec):
# on suppose que pop est une matrice avec deux colonnes homme, femme
# et que fec est une matrice avec une colonne fécondité
n = pop[:, 1] * fec[:, 0]
return n.sum()
nais = naissances(pop, mat_fec)
nais
756839.2760000001
Et on reprend la fonction iteration et le code de l’exercice précédent :
def iteration(pop, mortalite, fec, ratio):
pop_next = pop * (1 - mortalite)
nais = naissances(pop, fec)
row = numpy.array([[nais * ratio, nais * (1 - ratio)]])
pop_next = numpy.vstack([row, pop_next[:-1]]) # aucune naissance
return pop_next
popt = pop
for year in range(2020, 2101):
popt = iteration(popt, m, mat_fec, ratio)
if year == 2050:
popt2050 = popt.copy()
if year == 2100:
popt2100 = popt.copy()
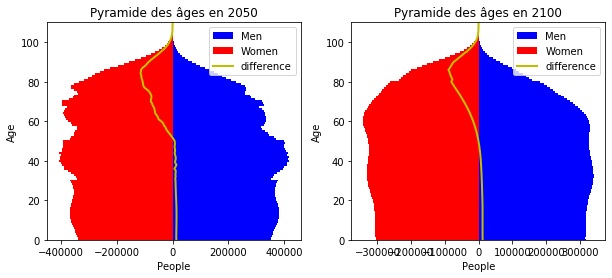
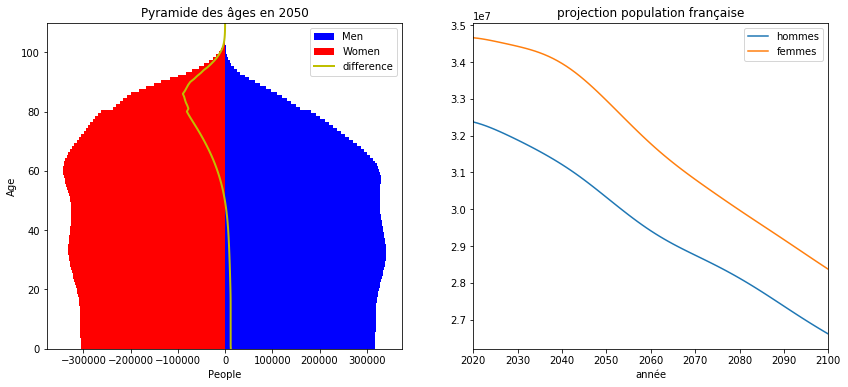
fig, ax = plt.subplots(1, 2, figsize=(10, 4))
plot_population_pyramid(popt2050[:, 0], popt2050[:, 1], ax=ax[0],
title="Pyramide des âges en 2050")
plot_population_pyramid(popt2100[:, 0], popt2100[:, 1], ax=ax[1],
title="Pyramide des âges en 2100");
On va plus loin et on stocke la population dans un vecteur :
total = [[2020, pop[:,0].sum(),pop[:,1].sum()]]
popt = pop
for year in range(2020, 2101):
popt = iteration(popt, m, mat_fec, ratio)
total.append([year, popt[:,0].sum(),popt[:,1].sum()])
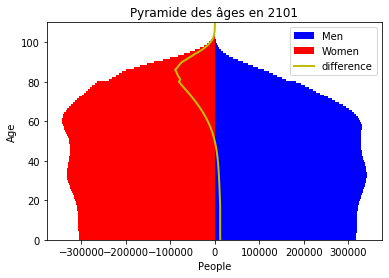
plot_population_pyramid(popt[:, 0], popt[:, 1], title="Pyramide des âges en 2101");
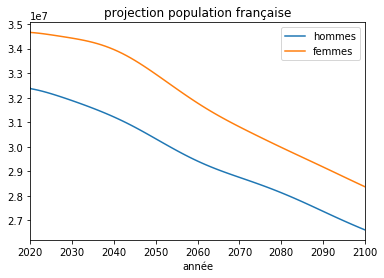
df = pandas.DataFrame(data=total, columns=["année","hommes","femmes"])
df.plot(x="année", y=["hommes", "femmes"], title="projection population française");
Le code suivant permet de combiner les deux graphes sur la même ligne avec la fonction subplots :
from matplotlib import pyplot as plt
fig, ax = plt.subplots(1, 2, figsize=(14,6))
plot_population_pyramid(popt[:,0], popt[:,1], title="Pyramide des âges en 2050", ax=ax[0])
df.plot(x="année", y=["hommes", "femmes"], title="projection population française", ax=ax[1]);
Retraites#
La réforme de la retraite en 2019 laissera un souvenir indélébile. Une des mesures far est celle de l’âge pivot. Le modèle développé jusqu’à présent ne permet pas de simuler ce que chaque français pourrait obtenir avec la nouvelle réforme mais il permet de donner un ordre de grandeur sur le nombre de retraités selon que l’âge pivot est de 62 ans ou plus vieux. Si on en croit cette page 1,7 actif cotisant par retraité, il y a 1,7 cotisant par retraité.
Trois populations sont considérées : les jeunes de moins de 21 ans, à la charge de leurs aînés, les actifs, les retraités dont le nombre dépend de l’âge pivot. on veut donc calculer l’évolution de ces trois populations.
from tqdm import tqdm
evol = []
popt = pop0.copy()
age_etude = 23
pivot = list(range(60, 68))
for year in tqdm(range(2020, 2101)):
popt = iteration(popt, m, mat_fec, ratio)
jeune = popt[:age_etude + 1].sum()
row = dict(year=year)
for p in pivot:
actif = popt[age_etude + 1:p].sum()
retraite = popt[p:].sum()
rt = actif / retraite
row['r%d' % p] = rt
evol.append(row)
df_evol = pandas.DataFrame(evol)
df_evol.head()
100%|████████████████████████████████████████████████████████████████████████████████| 81/81 [00:00<00:00, 6769.86it/s]
| year | r60 | r61 | r62 | r63 | r64 | r65 | r66 | r67 | |
|---|---|---|---|---|---|---|---|---|---|
| 0 | 2020 | 1.661675 | 1.792986 | 1.936632 | 2.092034 | 2.262744 | 2.450994 | 2.659420 | 2.893034 |
| 1 | 2021 | 1.637597 | 1.766554 | 1.907657 | 2.062432 | 2.230352 | 2.415367 | 2.620045 | 2.847438 |
| 2 | 2022 | 1.616615 | 1.742623 | 1.881228 | 2.033293 | 2.200564 | 2.382585 | 2.583765 | 2.807077 |
| 3 | 2023 | 1.593194 | 1.720874 | 1.856290 | 2.005630 | 2.169929 | 2.351192 | 2.549055 | 2.768466 |
| 4 | 2024 | 1.572343 | 1.698854 | 1.836163 | 1.982169 | 2.143622 | 2.321765 | 2.518906 | 2.734809 |
ax = df_evol.plot(x="year", y=["r%d" % p for p in pivot], figsize=(10, 4))
years = df_evol.year
ax.plot(years, [1.7 for _ in years], 'b--')
ax.set_title("Ratio actifs / retraités en fonction de l'âge pivot");
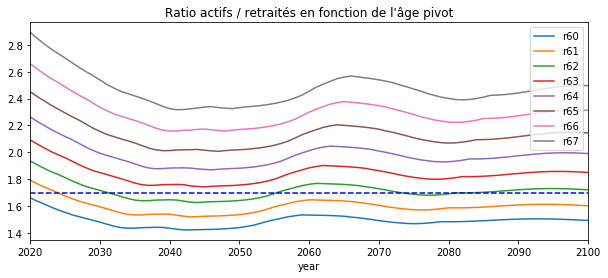
D’après ces simulations, il faudrait reculer l’âge de la retraite de deux ou trois ans pour garder le même ratio entre actifs et retraités tel qu’il est aujourd’hui.