Gradient Boosting#
Links: notebook, html, python, slides, GitHub
Le notebook explore l’algorithme du Gradient Boosting.
from jyquickhelper import add_notebook_menu
add_notebook_menu()
%matplotlib inline
Premier exemple#
On considère les paramètres par défaut de la classe GradientBoostingRegressor.
from numpy.random import randn, random
from pandas import DataFrame
from sklearn.model_selection import train_test_split
rnd = randn(1000)
X = random(1000) * 8 - 4
y = X ** 2 - X + rnd * 2 + 150 # X^2 - X + 150 + epsilon
X = X.reshape((-1, 1))
X_train, X_test, y_train, y_test = train_test_split(X, y)
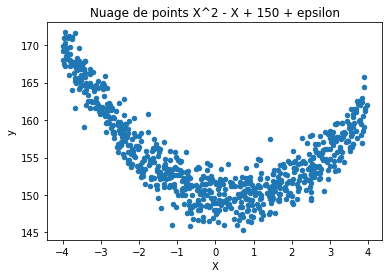
df = DataFrame({'X': X_train.ravel(), 'y': y_train})
ax = df.plot(x='X', y='y', kind='scatter')
ax.set_title("Nuage de points X^2 - X + 150 + epsilon");
from sklearn.ensemble import GradientBoostingRegressor
model = GradientBoostingRegressor(max_depth=1)
model.fit(X_train, y_train)
GradientBoostingRegressor(alpha=0.9, ccp_alpha=0.0, criterion='friedman_mse',
init=None, learning_rate=0.1, loss='ls', max_depth=1,
max_features=None, max_leaf_nodes=None,
min_impurity_decrease=0.0, min_impurity_split=None,
min_samples_leaf=1, min_samples_split=2,
min_weight_fraction_leaf=0.0, n_estimators=100,
n_iter_no_change=None, presort='deprecated',
random_state=None, subsample=1.0, tol=0.0001,
validation_fraction=0.1, verbose=0, warm_start=False)
import numpy
ind = numpy.argsort(X_test, axis=0)
y_ = model.predict(X_test)
df = DataFrame({'X': X_test[ind].ravel(),
'y': y_test[ind].ravel(),
'y^': y_[ind].ravel()})
ax = df.plot(x='X', y='y', kind='scatter')
df.plot(x='X', y='y^', kind='line', ax=ax, color="r")
ax.set_title("Prédictions avec GradientBoostingRegressor");
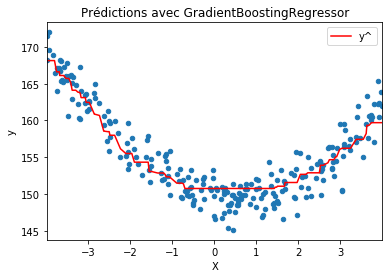
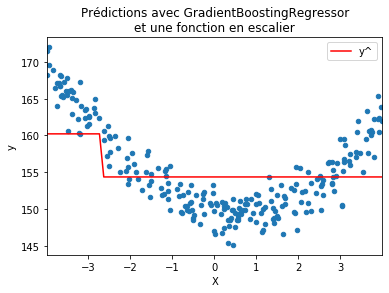
Rien d’imprévu jusque là. Essayons autre chose. On regarde avec une seule itération.
model = GradientBoostingRegressor(max_depth=1, n_estimators=1, learning_rate=0.5)
model.fit(X_train, y_train)
GradientBoostingRegressor(alpha=0.9, ccp_alpha=0.0, criterion='friedman_mse',
init=None, learning_rate=0.5, loss='ls', max_depth=1,
max_features=None, max_leaf_nodes=None,
min_impurity_decrease=0.0, min_impurity_split=None,
min_samples_leaf=1, min_samples_split=2,
min_weight_fraction_leaf=0.0, n_estimators=1,
n_iter_no_change=None, presort='deprecated',
random_state=None, subsample=1.0, tol=0.0001,
validation_fraction=0.1, verbose=0, warm_start=False)
y_ = model.predict(X_test)
df = DataFrame({'X': X_test[ind].ravel(),
'y': y_test[ind].ravel(),
'y^': y_[ind].ravel()})
ax = df.plot(x='X', y='y', kind='scatter')
df.plot(x='X', y='y^', kind='line', ax=ax, color="r")
ax.set_title("Prédictions avec GradientBoostingRegressor\net une fonction en escalier");
Essayons de montrer l’évolution de la courbe prédite en fonction du nombre de marches et revenons à 100 estimateurs.
model = GradientBoostingRegressor(max_depth=1)
model.fit(X_train, y_train)
GradientBoostingRegressor(alpha=0.9, ccp_alpha=0.0, criterion='friedman_mse',
init=None, learning_rate=0.1, loss='ls', max_depth=1,
max_features=None, max_leaf_nodes=None,
min_impurity_decrease=0.0, min_impurity_split=None,
min_samples_leaf=1, min_samples_split=2,
min_weight_fraction_leaf=0.0, n_estimators=100,
n_iter_no_change=None, presort='deprecated',
random_state=None, subsample=1.0, tol=0.0001,
validation_fraction=0.1, verbose=0, warm_start=False)
for i in range(0, model.estimators_.shape[0] + 1, 10):
if i == 0:
df = DataFrame({'X': X_test[ind].ravel(),
'y': y_test[ind].ravel()})
ax = df.plot(x='X', y='y', kind='scatter', figsize=(10, 4))
y_ = model.init_.predict(X_test)
color = 'b'
else:
y_ = sum([model.init_.predict(X_test)] +
[model.estimators_[k, 0].predict(X_test) * model.learning_rate
for k in range(0, i)])
color = 'r'
df = DataFrame({'X': X_test[ind].ravel(),
'y^': y_[ind].ravel()})
df.plot(x='X', y='y^', kind='line', ax=ax, color=color, label='i=%d' % i)
ax.set_title("Prédictions");
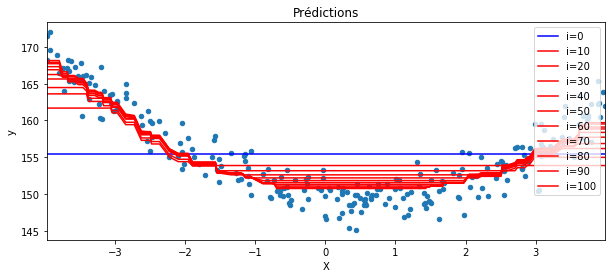
learning rate et itérations#
Et si on choisissait un learning_rate, plus petit ou plus grand…
model01 = GradientBoostingRegressor(max_depth=1, learning_rate=0.01)
model01.fit(X_train, y_train)
modela = GradientBoostingRegressor(max_depth=1, learning_rate=1.2)
modela.fit(X_train, y_train)
modelb = GradientBoostingRegressor(max_depth=1, learning_rate=1.99)
modelb.fit(X_train, y_train)
GradientBoostingRegressor(alpha=0.9, ccp_alpha=0.0, criterion='friedman_mse',
init=None, learning_rate=1.99, loss='ls', max_depth=1,
max_features=None, max_leaf_nodes=None,
min_impurity_decrease=0.0, min_impurity_split=None,
min_samples_leaf=1, min_samples_split=2,
min_weight_fraction_leaf=0.0, n_estimators=100,
n_iter_no_change=None, presort='deprecated',
random_state=None, subsample=1.0, tol=0.0001,
validation_fraction=0.1, verbose=0, warm_start=False)
import matplotlib.pyplot as plt
fig, ax = plt.subplots(1, 3, figsize=(12, 4))
ind = numpy.argsort(X_test, axis=0)
for i, mod in enumerate([model01, modela, modelb]):
df = DataFrame({'X': X_test[ind].ravel(),
'y': y_test[ind].ravel(),
'y^': mod.predict(X_test)[ind].ravel()})
df.plot(x='X', y='y', kind='scatter', ax=ax[i])
df.plot(x='X', y='y^', kind='line', ax=ax[i], color="r")
ax[i].set_title("learning_rate=%f" % mod.learning_rate);
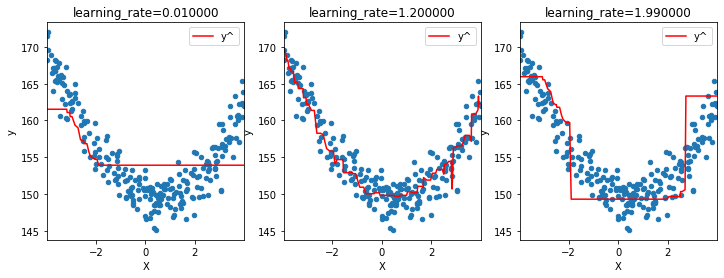
Une trop faible valeur de learning_rate semble retenir le modèle de converger, une grande valeur produit des effets imprévisibles. Pour comprendre pourquoi, il faut détailler l’algorithme…
L’algorithme#
Inspiration#
L’algorithme est inspiré de l’algorithme de la descente de gradient. On
considère une fonction réelle et on calcule le gradient
pour construire une suite :
La suite converge vers le minimum de la fonction
. On applique cela à une fonction d’erreur issue d’un problème
de régression.
Le plus souvent, on applique cette méthode à une fonction qui
dépend d’un paramètre
Et c’est la suite
qui converge vers le minimum de la fonction
de sorte que la
fonction
approxime au mieux les points
. Mais, on pourrait tout-à-fait résoudre ce problème
dans un espace de fonctions et non un espace de paramètres :
Le gradient est facile à calculer
puisqu’il ne dépend pas de
. On pourrait donc construire la
fonction de régression
comme une suite additive de fonctions
.
Et nous pourrions construire la fonction comme solution d’un
problème de régression défini par les couples
avec :
Voilà l’idée.
Algorithme#
Je reprends ici la page wikipedia. On cherche à construire un modèle qui
minimise l’erreur . On
note
le learning rate.
Etape 1 : on cale un premier modèle de régression, ici, simplement
une constante, en optimisant
.
est une constante.
On note ensuite
où
est la fonction constante construire lors de la
première étape.
Etape 2 : on calcule ensuite les erreurs
et l’opposé du gradient
Etape 3 : on choisit la fonction de telle sorte
qu’elle approxime au mieux les résidus
.
Etape 4 : on choisit le coefficient de telle
sorte qu’il minimise l’expression
.
On retourne l’étape 2 autant de fois qu’il y a d’itérations. Lorsque
l’erreur est une erreur quadratique , les
résidus deviennent
. Par conséquent,
la fonction
approxime au mieux ce qu’il manque pour atteindre
l’objectif. Un learning rate égal à 1 fait que la somme des prédictions
de chaque fonction
oscille autour de la vraie valeur, une
faible valeur donne l’impression d’une fonction qui converge à petits
pas, une grande valeur accroît l’amplitude des oscillations au point
d’empêcher l’algorithme de converger.
On voit aussi que l’algorithme s’intéresse d’abord aux points où le gradient est le plus fort, donc en principe aux erreurs les plus grandes.
Régression quantile#
Dans ce cas, l’erreur quadratique est remplacée par une erreur en valeur absolue. Les résidus dans ce cas sont égaux à -1 ou 1.
alpha = 0.5
model = GradientBoostingRegressor(alpha=alpha, loss='quantile', max_depth=1, learning_rate=0.1)
model.fit(X_train, y_train)
model01 = GradientBoostingRegressor(alpha=alpha, loss='quantile', max_depth=1, learning_rate=0.01)
model01.fit(X_train, y_train)
modela = GradientBoostingRegressor(alpha=alpha, loss='quantile', max_depth=1, learning_rate=1.2)
modela.fit(X_train, y_train)
modelb = GradientBoostingRegressor(alpha=alpha, loss='quantile', max_depth=1, learning_rate=1.99)
modelb.fit(X_train, y_train)
modelc = GradientBoostingRegressor(alpha=alpha, loss='quantile', max_depth=1, learning_rate=2.01)
modelc.fit(X_train, y_train)
GradientBoostingRegressor(alpha=0.5, ccp_alpha=0.0, criterion='friedman_mse',
init=None, learning_rate=2.01, loss='quantile',
max_depth=1, max_features=None, max_leaf_nodes=None,
min_impurity_decrease=0.0, min_impurity_split=None,
min_samples_leaf=1, min_samples_split=2,
min_weight_fraction_leaf=0.0, n_estimators=100,
n_iter_no_change=None, presort='deprecated',
random_state=None, subsample=1.0, tol=0.0001,
validation_fraction=0.1, verbose=0, warm_start=False)
fig, ax = plt.subplots(1, 5, figsize=(12, 4))
ind = numpy.argsort(X_test, axis=0)
for i, mod in enumerate([model, model01, modela, modelb, modelc]):
df = DataFrame({'X': X_test[ind].ravel(),
'y': y_test[ind].ravel(),
'y^': mod.predict(X_test)[ind].ravel()})
df.plot(x='X', y='y', kind='scatter', ax=ax[i])
df.plot(x='X', y='y^', kind='line', ax=ax[i], color="r")
ax[i].set_title("learning_rate=%1.2f" % mod.learning_rate);
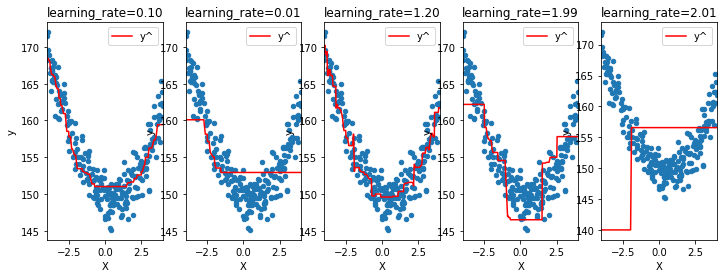
Concrètement, le paramètre max_depth=1 correspond à une simple
fonction et le modèle final est une
somme pondérée de fonctions indicatrices.
learning_rate et sur-apprentissage#
from sklearn.ensemble import RandomForestRegressor
from tqdm import tqdm
def experiment(models, tries=25):
scores = []
for _ in tqdm(range(tries)):
rnd = randn(1000)
X = random(1000) * 8 - 4
y = X ** 2 - X + rnd * 2 + 150 # X^2 - X + 150 + epsilon
X = X.reshape((-1, 1))
X_train, X_test, y_train, y_test = train_test_split(X, y)
scs = []
for model in models:
model.fit(X_train, y_train)
sc = model.score(X_test, y_test)
scs.append(sc)
scores.append(scs)
return scores
scores = experiment([
GradientBoostingRegressor(max_depth=1, n_estimators=100),
RandomForestRegressor(max_depth=1, n_estimators=100)
])
scores[:3]
100%|██████████| 25/25 [00:07<00:00, 3.33it/s]
[[0.8694704613325202, 0.6154817789660219],
[0.8483182026025287, 0.5448822271424512],
[0.8461792771831131, 0.4989444940263401]]
fig, ax = plt.subplots(1, 1, figsize=(10, 4))
ax.plot([_[0] for _ in scores], label="GradientBoostingRegressor")
ax.plot([_[1] for _ in scores], label="RandomForestRegressor")
ax.set_title("Comparaison pour une somme pondérée de fonctions en escalier")
ax.legend();
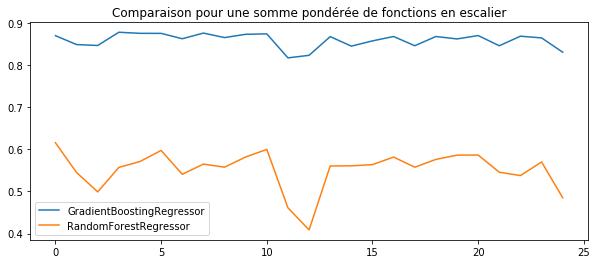
Ce résultat est attendu car la forêt aléatoire est une moyenne de modèle de régression tous appris dans les mêmes conditions alors que le gradient boosting s’intéresse à l’erreur après la somme des premiers régresseurs. Voyons avec des arbres de décision et non plus des fonctions en escaliers.
from sklearn.tree import DecisionTreeRegressor
scores = experiment([
GradientBoostingRegressor(max_depth=5, n_estimators=100),
RandomForestRegressor(max_depth=5, n_estimators=100),
DecisionTreeRegressor(max_depth=5)
])
100%|██████████| 25/25 [00:09<00:00, 2.57it/s]
fig, ax = plt.subplots(1, 1, figsize=(10, 4))
ax.plot([_[0] for _ in scores], label="GradientBoostingRegressor")
ax.plot([_[1] for _ in scores], label="RandomForestRegressor")
ax.plot([_[2] for _ in scores], label="DecisionTreeRegressor")
ax.set_title("Comparaison pour une somme pondérée d'arbres de décisions")
ax.legend();
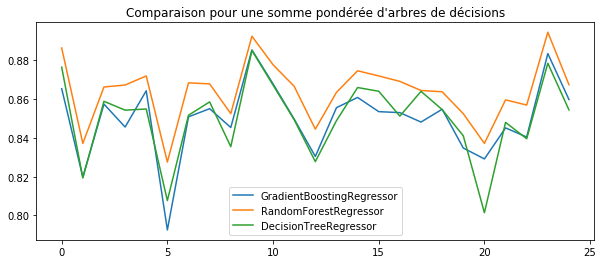
Le modèle GradientBoostingRegressor est clairement moins bon quand le modèle sous-jacent - l’arbre de décision - est performant. On voit que la forêt aléatoire est meilleure qu’un arbre de décision seul. Cela signifie qu’elle généralise mieux et que l’arbre de décision fait du sur apprentissage. De même, le GradientBoostingRegressor est plus exposé au sur-apprentissage.
scores = experiment([
RandomForestRegressor(max_depth=5, n_estimators=100),
GradientBoostingRegressor(max_depth=5, n_estimators=100, learning_rate=0.05),
GradientBoostingRegressor(max_depth=5, n_estimators=100, learning_rate=0.1),
GradientBoostingRegressor(max_depth=5, n_estimators=100, learning_rate=0.2),
])
scores[:2]
100%|██████████| 25/25 [00:15<00:00, 1.58it/s]
[[0.8775118863156427,
0.8658450142103171,
0.8606599637847404,
0.8364389493877071],
[0.8688453584981832,
0.8702540086892945,
0.8637637833529082,
0.8473494773500022]]
fig, ax = plt.subplots(1, 1, figsize=(10, 4))
ax.plot([_[0] for _ in scores], label="RandomForestRegressor")
ax.plot([_[1] for _ in scores], label="GBR(5, lr=0.05)")
ax.plot([_[2] for _ in scores], label="GBR(5, lr=0.1)")
ax.plot([_[3] for _ in scores], label="GBR(5, lr=0.2)")
ax.set_title("Comparaison pour différents learning_rate")
ax.legend();
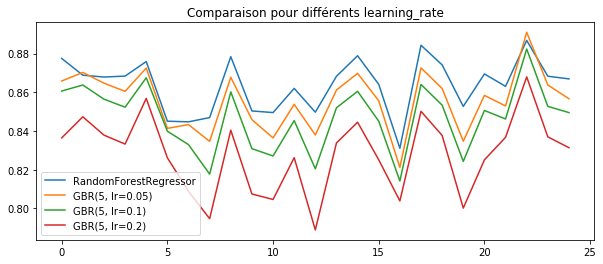
Diminuer learning_rate est clairement une façon d’éviter le sur-apprentissage mais les graphes précédents ont montré qu’il fallait plus d’itérations lorsque le learning rate est petit.
scores = experiment([
RandomForestRegressor(max_depth=5, n_estimators=100),
GradientBoostingRegressor(max_depth=1, n_estimators=100, learning_rate=0.05),
GradientBoostingRegressor(max_depth=1, n_estimators=100, learning_rate=0.1),
GradientBoostingRegressor(max_depth=1, n_estimators=100, learning_rate=0.2),
])
scores[:2]
100%|██████████| 25/25 [00:11<00:00, 2.30it/s]
[[0.8729919074479062,
0.8153190929633006,
0.8674320406867211,
0.8718834705539096],
[0.8442950556922886,
0.815363804525106,
0.8474302187940742,
0.8444000149837192]]
fig, ax = plt.subplots(1, 1, figsize=(10, 4))
ax.plot([_[0] for _ in scores], label="RandomForestRegressor")
ax.plot([_[1] for _ in scores], label="GBR(1, lr=0.05)")
ax.plot([_[2] for _ in scores], label="GBR(1, lr=0.1)")
ax.plot([_[3] for _ in scores], label="GBR(1, lr=0.2)")
ax.set_title("Comparaison pour différents learning_rate et des fonctions en escalier")
ax.legend();
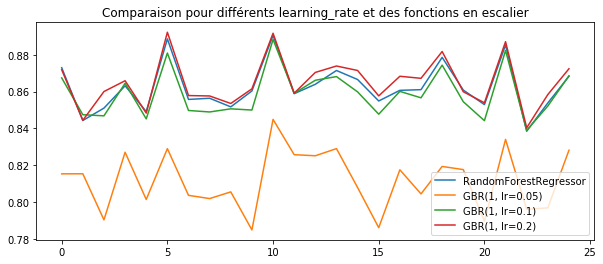
Plus le modèle sous-jacent est simple, plus le learning_rate peut être élevé car les modèles simples ne font pas de sur-apprentissage.
Gradient Boosting avec d’autres librairies#
Une somme pondérée de régression linéaire reste une regréssion linéaire. Il est impossible de tester ce scénario avec scikit-learn puisque seuls les arbres de décisions sont implémentés. Mais il existe d’autres librairies qui implémente le gradient boosting.
XGBoost#
from xgboost import XGBRegressor
scores = experiment([
RandomForestRegressor(max_depth=5, n_estimators=100),
XGBRegressor(max_depth=1, n_estimators=100, learning_rate=0.05, objective='reg:squarederror'),
XGBRegressor(max_depth=1, n_estimators=100, learning_rate=0.1, objective='reg:squarederror'),
XGBRegressor(max_depth=1, n_estimators=100, learning_rate=0.2, objective='reg:squarederror'),
])
scores[:2]
100%|██████████| 25/25 [00:08<00:00, 2.94it/s]
[[0.8679202687780997,
0.790334034357459,
0.8529726388853197,
0.8635076525988759],
[0.8714386434767272,
0.8076555688846012,
0.876320858210121,
0.8795969068127192]]
fig, ax = plt.subplots(1, 1, figsize=(10, 4))
ax.plot([_[0] for _ in scores], label="RandomForestRegressor(5)")
ax.plot([_[1] for _ in scores], label="XGB(1, lr=0.05)")
ax.plot([_[2] for _ in scores], label="XGB(1, lr=0.1)")
ax.plot([_[3] for _ in scores], label="XGB(1, lr=0.2)")
ax.set_title("Comparaison pour différents learning_rate\net des fonctions en escalier "
"avec XGBoost")
ax.legend();
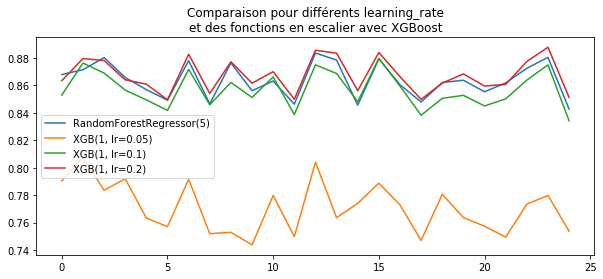
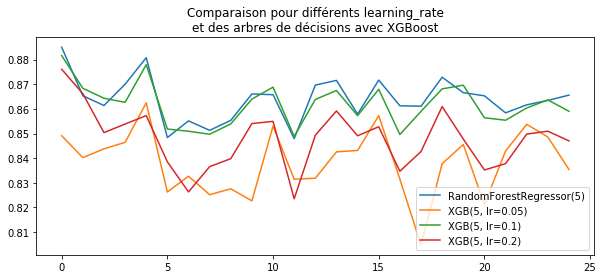
Les résultats sont sensiblement les mêmes.
scores = experiment([
RandomForestRegressor(max_depth=5, n_estimators=100),
XGBRegressor(max_depth=5, n_estimators=100, learning_rate=0.05, objective='reg:squarederror'),
XGBRegressor(max_depth=5, n_estimators=100, learning_rate=0.1, objective='reg:squarederror'),
XGBRegressor(max_depth=5, n_estimators=100, learning_rate=0.2, objective='reg:squarederror'),
])
scores[:2]
100%|██████████| 25/25 [00:10<00:00, 2.34it/s]
[[0.8850200020052564,
0.8491004361723402,
0.8816335539385363,
0.8760849465925536],
[0.8653185803997192,
0.8402218872212899,
0.8683639698989838,
0.8661907635378407]]
fig, ax = plt.subplots(1, 1, figsize=(10, 4))
ax.plot([_[0] for _ in scores], label="RandomForestRegressor(5)")
ax.plot([_[1] for _ in scores], label="XGB(5, lr=0.05)")
ax.plot([_[2] for _ in scores], label="XGB(5, lr=0.1)")
ax.plot([_[3] for _ in scores], label="XGB(5, lr=0.2)")
ax.set_title("Comparaison pour différents learning_rate\net des arbres de décisions "
"avec XGBoost")
ax.legend();
LightGbm#
from lightgbm import LGBMRegressor
scores = experiment([
RandomForestRegressor(max_depth=5, n_estimators=100),
LGBMRegressor(max_depth=1, n_estimators=100, learning_rate=0.05),
LGBMRegressor(max_depth=1, n_estimators=100, learning_rate=0.1),
LGBMRegressor(max_depth=1, n_estimators=100, learning_rate=0.2),
])
scores[:2]
100%|██████████| 25/25 [00:08<00:00, 3.03it/s]
[[0.8893616908044297,
0.8261124421322801,
0.8817998121916502,
0.8926218231962352],
[0.856474322673725,
0.7988728741682812,
0.8481012917344808,
0.8589885895995628]]
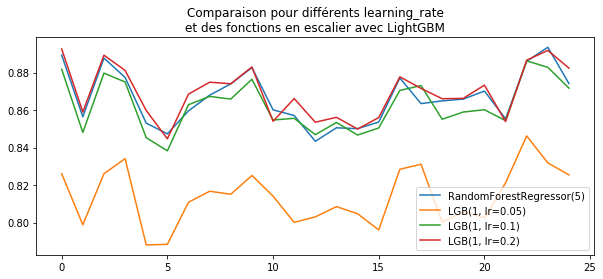
fig, ax = plt.subplots(1, 1, figsize=(10, 4))
ax.plot([_[0] for _ in scores], label="RandomForestRegressor(5)")
ax.plot([_[1] for _ in scores], label="LGB(1, lr=0.05)")
ax.plot([_[2] for _ in scores], label="LGB(1, lr=0.1)")
ax.plot([_[3] for _ in scores], label="LGB(1, lr=0.2)")
ax.set_title("Comparaison pour différents learning_rate\net des fonctions en escalier "
"avec LightGBM")
ax.legend();
scores = experiment([
RandomForestRegressor(max_depth=5, n_estimators=100),
LGBMRegressor(max_depth=5, n_estimators=100, learning_rate=0.05),
LGBMRegressor(max_depth=5, n_estimators=100, learning_rate=0.1),
LGBMRegressor(max_depth=5, n_estimators=100, learning_rate=0.2),
])
scores[:2]
100%|██████████| 25/25 [00:10<00:00, 2.26it/s]
[[0.8609320085819122,
0.8634839814757147,
0.8597595136945096,
0.8551285081930242],
[0.8326411682697042,
0.8292392382894543,
0.8280682654753115,
0.8224006022576665]]
fig, ax = plt.subplots(1, 1, figsize=(10, 4))
ax.plot([_[0] for _ in scores], label="RandomForestRegressor(5)")
ax.plot([_[1] for _ in scores], label="LGB(5, lr=0.05)")
ax.plot([_[2] for _ in scores], label="LGB(5, lr=0.1)")
ax.plot([_[3] for _ in scores], label="LGB(5, lr=0.2)")
ax.set_title("Comparaison pour différents learning_rate\net des arbres de décisions "
"avec LightGBM")
ax.legend();
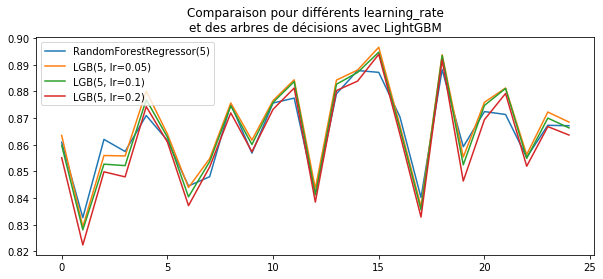
LightGBM paraît moins sensible au learning_rate que XGBoost.
CatBoost#
CatBoost est une des plus récentes. Elle est sensée être plus efficace pour les catégories ce qui n’est pas le cas ici.
from catboost import CatBoostRegressor
scores = experiment([
RandomForestRegressor(max_depth=5, n_estimators=100),
CatBoostRegressor(max_depth=1, n_estimators=100, learning_rate=0.05, verbose=False),
CatBoostRegressor(max_depth=1, n_estimators=100, learning_rate=0.1, verbose=False),
CatBoostRegressor(max_depth=1, n_estimators=100, learning_rate=0.2, verbose=False),
])
scores[:2]
100%|██████████| 25/25 [00:24<00:00, 1.00it/s]
[[0.8630013062715012,
0.8171496530214813,
0.8705211410285828,
0.8756897741529662],
[0.8655349009959259,
0.8082932897705987,
0.8614224979710696,
0.866454702226169]]
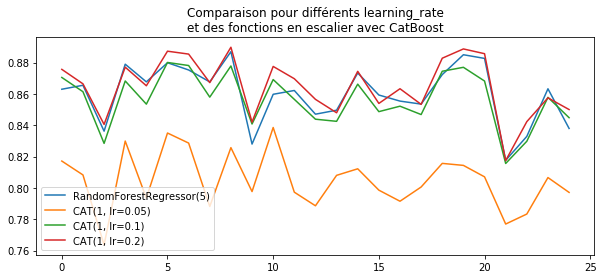
fig, ax = plt.subplots(1, 1, figsize=(10, 4))
ax.plot([_[0] for _ in scores], label="RandomForestRegressor(5)")
ax.plot([_[1] for _ in scores], label="CAT(1, lr=0.05)")
ax.plot([_[2] for _ in scores], label="CAT(1, lr=0.1)")
ax.plot([_[3] for _ in scores], label="CAT(1, lr=0.2)")
ax.set_title("Comparaison pour différents learning_rate\net des fonctions en escalier "
"avec CatBoost")
ax.legend();
scores = experiment([
RandomForestRegressor(max_depth=5, n_estimators=100),
CatBoostRegressor(max_depth=5, n_estimators=100, learning_rate=0.05, verbose=False),
CatBoostRegressor(max_depth=5, n_estimators=100, learning_rate=0.1, verbose=False),
CatBoostRegressor(max_depth=5, n_estimators=100, learning_rate=0.2, verbose=False),
])
scores[:2]
100%|██████████| 25/25 [00:31<00:00, 1.27s/it]
[[0.8225527835029143,
0.83387879282829,
0.8336031459553583,
0.8284593124477894],
[0.8662884568803738,
0.870941831673826,
0.8731751692649438,
0.8701201310203557]]
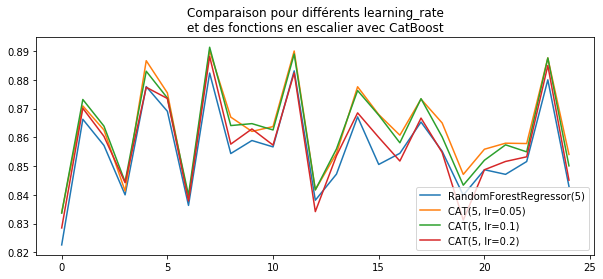
fig, ax = plt.subplots(1, 1, figsize=(10, 4))
ax.plot([_[0] for _ in scores], label="RandomForestRegressor(5)")
ax.plot([_[1] for _ in scores], label="CAT(5, lr=0.05)")
ax.plot([_[2] for _ in scores], label="CAT(5, lr=0.1)")
ax.plot([_[3] for _ in scores], label="CAT(5, lr=0.2)")
ax.set_title("Comparaison pour différents learning_rate\net des fonctions en escalier "
"avec CatBoost")
ax.legend();