1A.algo - Des problèmes de graphes#
Links: notebook, html, python, slides, GitHub
Découvrir les graphes avec des problèmes pas trop compliqués. Composantes connexes, plus court chemin et…
from jyquickhelper import add_notebook_menu
add_notebook_menu()
Un graphe#
# tutoriel_graphe
noeuds = {0: 'le', 1: 'silences', 2: 'quelques', 3: '\xe9crit', 4: 'non-dits.', 5: 'Et', 6: 'risque', 7: '\xe0', 8: "qu'elle,", 9: 'parfois', 10: 'aim\xe9', 11: 'lorsque', 12: 'que', 13: 'plus', 14: 'les', 15: 'Minelli,', 16: "n'oublierai", 17: 'je', 18: 'prises', 19: 'sa', 20: 'la', 21: 'jeune,', 22: "qu'elle,", 23: '\xe0', 24: 'ont', 25: "j'ai", 26: 'chemin', 27: '\xe9tranger', 28: 'lente', 29: 'de', 30: 'voir', 31: 'quand', 32: 'la', 33: 'recul,', 34: 'de', 35: 'trop', 36: 'ce', 37: 'Je', 38: 'Il', 39: "l'extr\xeame", 40: "J'ai", 41: 'silences,', 42: "qu'elle,", 43: 'le', 44: 'trace,', 45: 'avec', 46: 'seras', 47: 'dire,', 48: 'femme', 49: 'soit'}
arcs = {(3, 15): None, (46, 47): None, (42, 33): None, (35, 45): None, (1, 14): None, (22, 26): None, (26, 28): None, (43, 29): None, (40, 41): None, (29, 44): None, (17, 3): None, (32, 37): None, (24, 19): None, (46, 34): None, (11, 19): None, (34, 49): None, (22, 2): None, (37, 48): None, (14, 12): None, (3, 10): None, (5, 18): None, (12, 24): None, (34, 32): None, (45, 39): None, (37, 26): None, (33, 45): None, (34, 47): None, (36, 31): None, (29, 47): None, (13, 11): None, (12, 21): None, (2, 16): None, (5, 4): None, (33, 35): None, (28, 49): None, (25, 49): None, (21, 0): None, (3, 13): None, (18, 24): None, (12, 7): None, (13, 15): None, (11, 1): None, (16, 23): None, (37, 45): None, (27, 32): None, (32, 41): None, (8, 24): None, (10, 1): None, (2, 24): None, (24, 11): None, (2, 14): None, (47, 36): None, (48, 39): None, (30, 25): None, (30, 43): None, (15, 14): None, (26, 27): None, (6, 8): None, (20, 10): None, (19, 17): None, (5, 7): None, (44, 25): None, (27, 38): None, (2, 0): None, (3, 18): None, (3, 9): None, (25, 33): None, (42, 48): None, (2, 15): None, (26, 48): None, (26, 38): None, (7, 8): None, (8, 4): None}
from mlstatpy.graph.graphviz_helper import draw_graph_graphviz
draw_graph_graphviz(noeuds, arcs, "image.png")
from IPython.display import Image
Image("image.png", width=400)
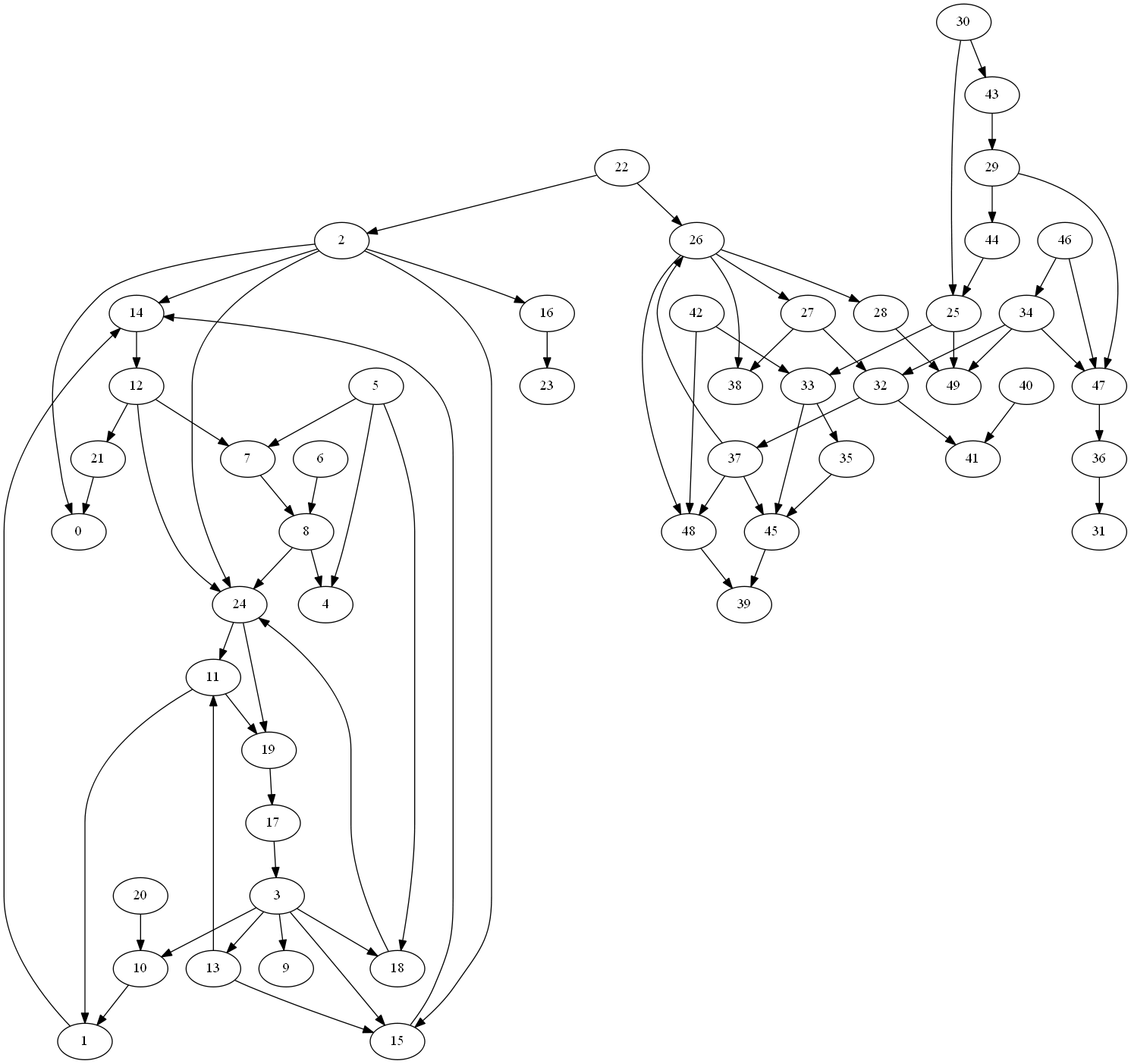
1. Composantes connexes#
Un noeud permet de couper le graphe en deux. Trouverez-vous lequel ? Savez-vous calculer une composante connexe ?
2. Plus court chemin#
Prenez deux noeuds au hasard, déterminer le nombre d’arcs du chemin le plus court qui les relient.
3. Point central#
Déterminer le point par lequel passent le plus grand nombre de chemin les plus court. Un indice : Algorithme de Bellman-Ford.