2A.ml - Imbalanced dataset#
Links: notebook, html, python, slides, GitHub
Un jeu de données imbalanced signifie qu’une classe est sous représentée dans un problème de classification. Lire 8 Tactics to Combat Imbalanced Classes in Your Machine Learning Dataset.
from jyquickhelper import add_notebook_menu
add_notebook_menu()
%matplotlib inline
Génération de données#
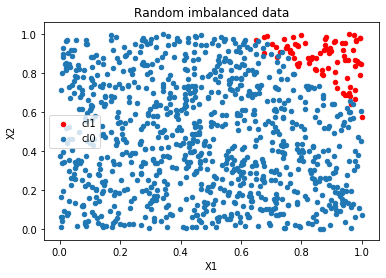
On génère un problème de classification binaire avec une classe sous représentée.
import numpy.random
import pandas
def generate_data(nb, ratio, noise):
mat = numpy.random.random((nb,2))
noise = numpy.random.random((mat.shape[0],1)) * noise
data = pandas.DataFrame(mat, columns=["X1", "X2"])
data["decision"] = data.X1 + data.X2 + noise.ravel()
vec = list(sorted(data["decision"]))
l = len(vec)- 1 - int(len(vec) * ratio)
seuil = vec[l]
data["cl"] = data["decision"].apply(lambda r: 1 if r > seuil else 0)
from sklearn.utils import shuffle
data = shuffle(data)
return data
data = generate_data(1000, 0.08, 0.1)
data.describe()
| X1 | X2 | decision | cl | |
|---|---|---|---|---|
| count | 1000.000000 | 1000.000000 | 1000.000000 | 1000.000000 |
| mean | 0.501011 | 0.497330 | 1.047568 | 0.080000 |
| std | 0.281113 | 0.295740 | 0.410862 | 0.271429 |
| min | 0.001387 | 0.001413 | 0.032132 | 0.000000 |
| 25% | 0.274936 | 0.238735 | 0.776950 | 0.000000 |
| 50% | 0.505160 | 0.491212 | 1.025373 | 0.000000 |
| 75% | 0.729076 | 0.752400 | 1.340745 | 0.000000 |
| max | 0.999988 | 0.999728 | 2.048328 | 1.000000 |
ax = data[data.cl==1].plot(x="X1", y="X2", kind="scatter", label="cl1", color="r")
data[data.cl==0].plot(x="X1", y="X2", kind="scatter", label="cl0", ax=ax)
ax.set_title("Random imbalanced data");
from sklearn.model_selection import train_test_split
while True:
X_train, X_test, y_train, y_test = train_test_split(data[["X1", "X2"]], data["cl"])
if sum(y_test) > 0:
break
Le découpage apprentissage est délicat car il n’y pas beaucoup d’exemples pour la classe sous-représentée.
y_test.sum()
22
Apprendre et tester un modèle#
Pour ce type de problème, un modèle qui retourne la classe majoritaire quelque soit le cas est déjà un bon modèle puisqu’il retourne la bonne réponse dans la majorité des cas.
from sklearn.metrics import confusion_matrix
def confusion(model, X_train, X_test, y_train, y_test):
model.fit(X_train, y_train)
predt = model.predict(X_train)
c_train = confusion_matrix(y_train, predt)
pred = model.predict(X_test)
c_test = confusion_matrix(y_test, pred)
return pandas.DataFrame(numpy.hstack([c_train, c_test]), index=["y=0", "y=1"],
columns="train:y=0 train:y=1 test:y=0 test:y=1".split())
from sklearn.linear_model import LogisticRegression
confusion(LogisticRegression(solver='lbfgs'),
X_train, X_test, y_train, y_test)
| train:y=0 | train:y=1 | test:y=0 | test:y=1 | |
|---|---|---|---|---|
| y=0 | 692 | 0 | 228 | 0 |
| y=1 | 34 | 24 | 12 | 10 |
Quelques exemples pour tester, quelques exemples pour apprendre. C’est peu.
from sklearn.tree import DecisionTreeClassifier
confusion(DecisionTreeClassifier(), X_train, X_test, y_train, y_test)
| train:y=0 | train:y=1 | test:y=0 | test:y=1 | |
|---|---|---|---|---|
| y=0 | 692 | 0 | 227 | 1 |
| y=1 | 0 | 58 | 2 | 20 |
from sklearn.ensemble import RandomForestClassifier
confusion(RandomForestClassifier(n_estimators=10),
X_train, X_test, y_train, y_test)
| train:y=0 | train:y=1 | test:y=0 | test:y=1 | |
|---|---|---|---|---|
| y=0 | 692 | 0 | 227 | 1 |
| y=1 | 1 | 57 | 2 | 20 |
L’algorithme de la régression logistique converge plus difficile que celui des arbres de décision. Voyons comment cela évolue entre de la norme L1 ou L2 et de la proportion de la classe mal balancée.
ratio = list(_/400.0 for _ in range(1, 101))
rows = []
for r in ratio:
data = generate_data(1000, r, noise=0.0)
while True:
X_train, X_test, y_train, y_test = train_test_split(data[["X1", "X2"]], data["cl"])
if sum(y_test) > 0 and sum(y_train) > 0:
break
c = confusion(LogisticRegression(penalty='l1', solver='liblinear'),
X_train, X_test, y_train, y_test)
c0, c1 = c.loc["y=1", "test:y=0"], c.loc["y=1", "test:y=1"]
row = dict(ratio=r, precision_l1=c1 / (c0 + c1) )
c = confusion(LogisticRegression(penalty='l2', solver="liblinear"),
X_train, X_test, y_train, y_test)
c0, c1 = c.loc["y=1", "test:y=0"], c.loc["y=1", "test:y=1"]
row["precision_l2"] = c1 / (c0 + c1)
rows.append(row)
df = pandas.DataFrame(rows)
import matplotlib.pyplot as plt
fig, ax = plt.subplots(1, 1)
df.plot(x="ratio", y=[_ for _ in df.columns if _ !="ratio"], ax=ax)
ax.set_xlabel("Ratio classe mal balancée")
ax.set_ylabel("Précision pour la classe 1 (petite classe)");
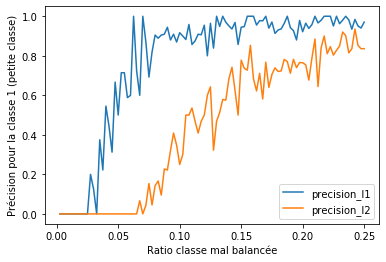
La norme l1 est plus sensible aux petites classes. La métrique balanced_accuracy_score calcule la performance du modèle en donnant le même poids quelque soit la taille de la classe, il fait la moyenne de l’accuracy par classe.
from sklearn.metrics import balanced_accuracy_score, accuracy_score
ratio = list(_/400.0 for _ in range(1, 101))
rows = []
for r in ratio:
data = generate_data(1000, r, noise=0.0)
while True:
X_train, X_test, y_train, y_test = train_test_split(data[["X1", "X2"]], data["cl"])
if sum(y_test) > 0 and sum(y_train) > 0:
break
model = LogisticRegression(penalty='l2', solver='liblinear')
model.fit(X_train, y_train)
predt = model.predict(X_test)
bacc_l2 = balanced_accuracy_score(y_test, predt)
acc_l2 = accuracy_score(y_test, predt)
model = LogisticRegression(penalty='l1', solver='liblinear')
model.fit(X_train, y_train)
predt = model.predict(X_test)
bacc_l1 = balanced_accuracy_score(y_test, predt)
acc_l1 = accuracy_score(y_test, predt)
row = dict(standard_l2=acc_l2, balanced_l2=bacc_l2, ratio=r,
standard_l1=acc_l1, balanced_l1=bacc_l1)
rows.append(row)
df = pandas.DataFrame(rows)
fig, ax = plt.subplots(1, 1)
df.plot(x="ratio", y=[_ for _ in df.columns if _ !="ratio"], ax=ax)
ax.set_xlabel("Ratio classe mal balancée")
ax.set_ylabel("Accuracy");
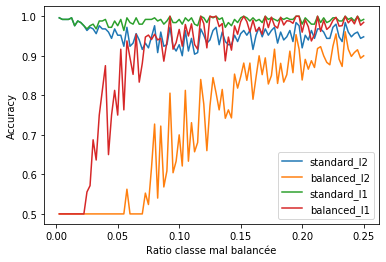
La métrique classique “accuracy” ne permet pas de détecter un problème de classification lorsqu’une classe est mal balancée car chaque exemple est pondéré de la même façon. L’accuracy est donc très proche de celle obtenue sur la classe majoritaire.
from sklearn.ensemble import AdaBoostClassifier
ratio = list(_/400.0 for _ in range(1, 101))
rows = []
for r in ratio:
data = generate_data(1000, r, noise=0.0)
while True:
X_train, X_test, y_train, y_test = train_test_split(data[["X1", "X2"]], data["cl"])
if sum(y_test) > 0 and sum(y_train) > 0:
break
c = confusion(LogisticRegression(penalty='l1', solver="liblinear"),
X_train, X_test, y_train, y_test)
c0, c1 = c.loc["y=1", "test:y=0"], c.loc["y=1", "test:y=1"]
row = dict(ratio=r, precision_l1=c1 / (c0 + c1) )
c = confusion(LogisticRegression(penalty='l2', solver="liblinear"),
X_train, X_test, y_train, y_test)
c0, c1 = c.loc["y=1", "test:y=0"], c.loc["y=1", "test:y=1"]
row["precision_l2"] = c1 / (c0 + c1)
c = confusion(AdaBoostClassifier(LogisticRegression(penalty='l2', solver="liblinear"),
algorithm="SAMME.R", n_estimators=50,
learning_rate=3),
X_train, X_test, y_train, y_test)
c0, c1 = c.loc["y=1", "test:y=0"], c.loc["y=1", "test:y=1"]
row["pre_AdaBoost_l2-50"] = c1 / (c0 + c1)
c = confusion(AdaBoostClassifier(LogisticRegression(penalty='l2', solver="liblinear"),
algorithm="SAMME.R", n_estimators=100,
learning_rate=3),
X_train, X_test, y_train, y_test)
c0, c1 = c.loc["y=1", "test:y=0"], c.loc["y=1", "test:y=1"]
row["prec_AdaBoost_l2-100"] = c1 / (c0 + c1)
rows.append(row)
df = pandas.DataFrame(rows)
fig, ax = plt.subplots(1, 1)
df.plot(x="ratio", y=[_ for _ in df.columns if _ != "ratio"], ax=ax)
ax.set_xlabel("Ratio classe mal balancée")
ax.set_ylabel("Précision pour la classe 1 (petite classe)");
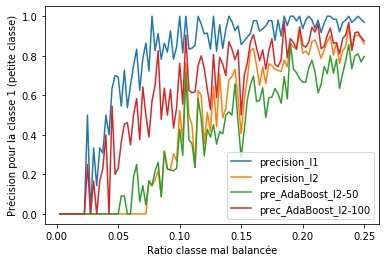
On voit que l’algorithme AdaBoost permet de favoriser les petites classes mais il faut jouer avec le learning rate et le nombre d’estimateurs.
from sklearn.ensemble import AdaBoostClassifier
ratio = list(_/400.0 for _ in range(1, 101))
rows = []
for r in ratio:
data = generate_data(1000, r, noise=0.0)
while True:
X_train, X_test, y_train, y_test = train_test_split(data[["X1", "X2"]], data["cl"])
if sum(y_test) > 0 and sum(y_train) > 0:
break
c = confusion(DecisionTreeClassifier(),
X_train, X_test, y_train, y_test)
c0, c1 = c.loc["y=1", "test:y=0"], c.loc["y=1", "test:y=1"]
row = dict(ratio=r, precision_tree=c1 / (c0 + c1) )
c = confusion(RandomForestClassifier(n_estimators=10),
X_train, X_test, y_train, y_test)
c0, c1 = c.loc["y=1", "test:y=0"], c.loc["y=1", "test:y=1"]
row["precision_rf"] = c1 / (c0 + c1)
rows.append(row)
fig, ax = plt.subplots(1, 1)
df = pandas.DataFrame(rows)
df.plot(x="ratio", y=[_ for _ in df.columns if _ != "ratio"], ax=ax)
ax.set_xlabel("Ratio classe mal balancée")
ax.set_ylabel("Précision pour la classe 1 (petite classe)");
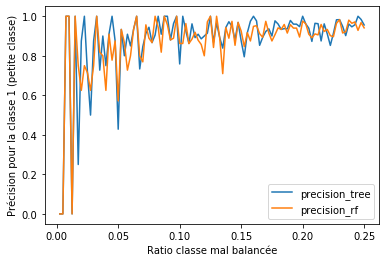
Les méthodes ensemblistes fonctionnent mieux dans ce cas car
l’algorithme cherche la meilleure séparation entre deux classes de façon
à ce que les deux classes soient de chaque côté de cette frontière. La
proportion d’exemples a moins d’importance pour le critère de
Gini. Dans
l’exemple suivant, on trie selon la variable et on cherche
la meilleur séparation
data = generate_data(100, 0.08, 0.1).values
data.sort(axis=0)
data[:5]
array([[0.0133622 , 0.00996042, 0.04423642, 0. ],
[0.0215605 , 0.0276332 , 0.21230519, 0. ],
[0.02827806, 0.03093092, 0.2737886 , 0. ],
[0.03648334, 0.03178925, 0.31218421, 0. ],
[0.03649288, 0.03712127, 0.34506943, 0. ]])
from ensae_teaching_cs.ml.gini import gini
def gini_gain_curve(Y):
"le code n'est pas le plus efficace du monde mais ça suffira"
g = gini(Y)
curve = numpy.empty((len(Y),))
for i in range(1, len(Y)-1):
g1 = gini(Y[:i])
g2 = gini(Y[i:])
curve[i] = g - (g1 + g2) / 2
return curve
gini_gain_curve([0, 1, 0, 1, 1, 1, 1])
array([5.20836364e+01, 9.52380952e-03, 4.28571429e-02, 1.26190476e-01,
4.28571429e-02, 2.61904762e-02, 2.55640000e+02])
from ensae_teaching_cs.ml.gini import gini
gini(data[:, 3])
0.9550000000000001
fig, ax = plt.subplots(1, 1)
for skew in [0.05, 0.1, 0.15, 0.2, 0.25, 0.5]:
data = generate_data(100, skew, 0.1).values
data.sort(axis=0)
ax.plot(gini_gain_curve(data[:, 3]), label="balance=%f" % skew)
ax.legend()
ax.set_title("Gini gain for different class proportion")
ax.set_ylabel("Gini")
ax.set_xlabel("x");
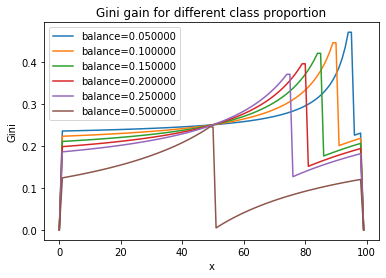
Ce n’est pas vraiment pas l’algorithme des arbres de décision mais l’idée est de montrer que les arbres de décision sont moins sensibles aux petites classes quand il s’agit de trouver la meilleure séparation. Et c’est nécessaire car pour les branches les plus basses, tous les sous-échantillons qui terminent dans ces branches sont très mal balancés.
Exercice 1 : réduire les exemples loin des frontières#
Pour rééquilibrer la proportion des classes, on cherche à enlever des points de la base d’apprentissage pour lesquels il n’y a pas d’ambiguïté, c’est-à-dire loin des frontières. Imaginer une solution à l’aides des k plus proches voisins.
Exercice 2 : multiplier les exemples#
L’idée est d’utiliser une technique pour multiplier les exemples de la
classe sous-représentée sans pour autant avoir des exemples exactement
identiques. On utilise l’algorithme
SMOTE. En résumé,
l’algorithme consiste à créer des exemples pour la classe
sous-représentée. On choisit un de ces exemples . Pour cet
, on calcule ses
plus proches voisins dans la base
d’apprentissage, toutes classes comprises. On choisit un voisin
aléatoire
parmi les
voisins. On tire un nombre
aléaloire
. Le nouvel élément ajouté à la base
d’apprentissage est
et il est associé à la classe
sous-représentée. On continue jusqu’à la proportion souhaitée.
Exercice 3 : essai du module imbalanced#
Ce module implémente différentes façons de gérer les classes sous et sur-représentées.
Exercice 4 : validation croisée#
Lorsqu’une classe est sous représentée, la validation croisée doit être
effectuée sous contrainte. Si elle est réalisée de façon complètement
aléatoire, il est probable que la classe sous représentée ne soit pas
présente. Si la classe 0 possède exemples parmi
,
quelle est la distribution du minimum d’observations dans une des
clasees ? Il veut comparer une crossvalidation classique avec un
échantillon stratigiée
(StratifiedKFold).