2A.ml - Arbres de décision / Random Forest - correction#
Links: notebook, html, python, slides, GitHub
Méthodes ensemblistes, features importance, correction.
%matplotlib inline
import matplotlib.pyplot as plt
from jyquickhelper import add_notebook_menu
add_notebook_menu()
Données#
Le code suivant télécharge les données nécessaires salaries2010.zip. On reprend le code qui permet d’obtenir les données (il faut l’exécuter avant chaque partie).
import os
if not os.path.exists("salaries2010.db3"):
import pyensae.datasource
db3 = pyensae.datasource.download_data("salaries2010.zip")
import sqlite3, pandas
con = sqlite3.connect("salaries2010.db3")
df = pandas.io.sql.read_sql("select * from varmod", con)
con.close()
values = df[ df.VARIABLE == "TRNETTOT"].copy()
def process_intervalle(s):
if "euros et plus" in s :
return float ( s.replace("euros et plus", "").replace(" ","") )
spl = s.split("à")
if len(spl) == 2 :
s1 = spl[0].replace("Moins de","").replace("euros","").replace(" ","")
s2 = spl[1].replace("Moins de","").replace("euros","").replace(" ","")
return (float(s1)+float(s2))/2
else :
s = spl[0].replace("Moins de","").replace("euros","").replace(" ","")
return float(s)/2
values["montant"] = values.apply(lambda r : process_intervalle(r ["MODLIBELLE"]), axis = 1)
con = sqlite3.connect("salaries2010.db3")
data = pandas.io.sql.read_sql("select TRNETTOT,AGE,SEXE,DEPT,DEPR,TYP_EMPLOI,PCS,CS,CONT_TRAV,CONV_COLL from salaries", con)
con.close()
salaires = data.merge ( values, left_on = "TRNETTOT", right_on="MODALITE" )
salaires.dropna(inplace=True)
salaires.head()
| TRNETTOT | AGE | SEXE | DEPT | DEPR | TYP_EMPLOI | PCS | CS | CONT_TRAV | CONV_COLL | VARIABLE | MODALITE | MODLIBELLE | montant | |
|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|
| 0 | 14 | 50.0 | 1 | 972 | O | 628G | 62 | ZZZ | TRNETTOT | 14 | 18 000 à 19 999 euros | 18999.5 | ||
| 1 | 14 | 41.0 | 1 | 75 | 75 | O | 354C | 35 | CDD | 1734 | TRNETTOT | 14 | 18 000 à 19 999 euros | 18999.5 |
| 2 | 14 | 29.0 | 1 | 75 | 75 | O | 373C | 37 | CDD | 0014 | TRNETTOT | 14 | 18 000 à 19 999 euros | 18999.5 |
| 3 | 14 | 30.0 | 1 | 75 | 75 | O | 651A | 65 | CDD | 9999 | TRNETTOT | 14 | 18 000 à 19 999 euros | 18999.5 |
| 4 | 14 | 55.0 | 1 | 78 | 92 | O | 623E | 62 | ZZZ | TRNETTOT | 14 | 18 000 à 19 999 euros | 18999.5 |
salaires.shape
(2191579, 14)
Exercice 1 : Bases d’apprentissage, test, courbes#
On ne considère qu’une partie de la base pour éviter de passer toute la séance à attendre les résultats :
import random
salaires["rnd"] = salaires.apply (lambda r : random.randint(0,50),axis=1)
ech = salaires [ salaires.rnd == 0 ]
X,Y = ech[["AGE","SEXE","TYP_EMPLOI","CONT_TRAV", "CS"]], ech[["montant"]]
Xd = X.T.to_dict().values()
X.shape
(43011, 5)
On transforme les variables sous forme de chaînes de caractères en variables binaires :
from sklearn.feature_extraction import DictVectorizer
prep = DictVectorizer()
Xt = prep.fit_transform(Xd).toarray()
On découpe la base en base d’apprentissage et test :
from sklearn.model_selection import train_test_split
a_train, a_test, b_train, b_test = train_test_split(Xt, Y, test_size=0.33)
Expérience 1#
On fait varier un paramètre et on observe l’erreur sur la base d’apprentissage et de test.
from sklearn.tree import DecisionTreeRegressor
import matplotlib.pyplot as plt
from sklearn.metrics import mean_squared_error
curves = []
for max_depth in range(1,10) :
clf = DecisionTreeRegressor(min_samples_leaf=10, max_depth=max_depth)
clf = clf.fit(a_train, b_train)
erra = mean_squared_error( clf.predict(a_train), b_train)**0.5
errb = mean_squared_error( clf.predict(a_test), b_test)**0.5
print("max_depth",max_depth, "erreur",erra,errb)
curves.append((max_depth, erra,errb, clf) )
plt.plot ( [c[0] for c in curves], [c[1] for c in curves], label="train")
plt.plot ( [c[0] for c in curves], [c[2] for c in curves], label="test")
plt.legend()
max_depth 1 erreur 10740.916668324217 10846.54435688257
max_depth 2 erreur 10060.820466095634 10157.555221393412
max_depth 3 erreur 9472.779130826442 9507.772616147568
max_depth 4 erreur 9120.442014667919 9202.244729398157
max_depth 5 erreur 8811.580728562523 8911.264282454193
max_depth 6 erreur 8594.15887402314 8736.88981562483
max_depth 7 erreur 8368.204499944435 8550.051902144827
max_depth 8 erreur 8210.109582518286 8426.738612833457
max_depth 9 erreur 8089.658523934697 8350.6372466417
<matplotlib.legend.Legend at 0x1ec99967780>
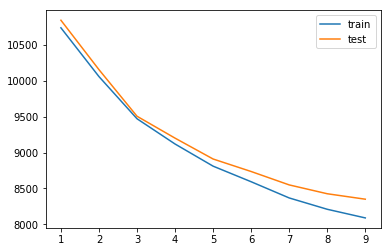
L’erreur sur la base de test baisse légèrement jusqu’à ce que l’arbre
ait une profondeur de 3 ou 4. C’est la taille de l’arbre qu’il faudrait
choisir et qu’on dessine en remplaçant les noms des variables X[i]
par des noms plus intelligibles.
import sys
cwd = os.getcwd()
if sys.platform.startswith("win"):
exe = 'C:\\Program Files (x86)\\Graphviz2.38\\bin\\dot.exe'
if not os.path.exists(exe):
raise FileNotFoundError(exe)
exe = '"{0}"'.format(exe)
else:
exe = "dot"
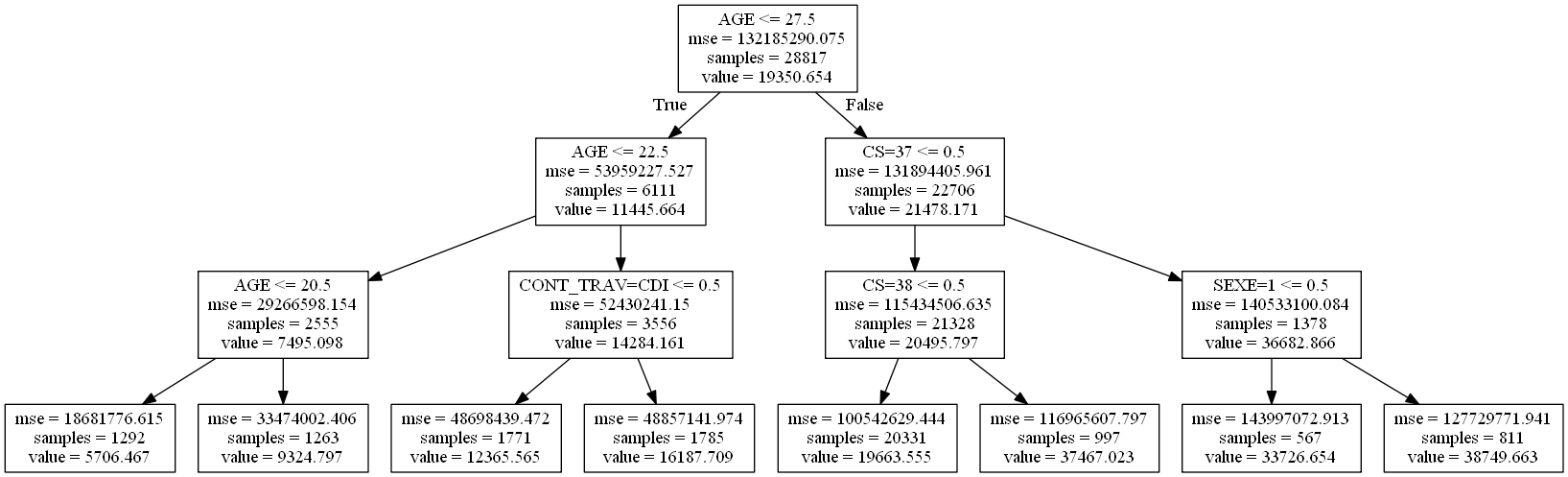
clf = curves[2][-1]
from sklearn.tree import export_graphviz
export_graphviz(clf, out_file="arbrec.dot")
# on remplace X[i] par les noms des variables
with open("arbrec.dot","r") as f:
text = f.read()
for i in range(len(prep.feature_names_)):
text=text.replace("X[{0}]".format(i), prep.feature_names_[i])
with open("arbrec.dot","w") as f:
f.write(text)
cwd = os.getcwd()
cmd = '"{0}" -Tpng {1}\\arbrec.dot -o {1}\\arbrec.png'.format(exe, cwd)
os.system(cmd)
from IPython.core.display import Image
Image("arbrec.png")
Version javascript :
from jyquickhelper import RenderJsVis
dot = export_graphviz(clf, out_file=None, feature_names=prep.feature_names_)
RenderJsVis(dot=dot, height="400px", layout='hierarchical')
Expérience 2#
On remplace l’arbre de décision par des random forest.
import random
salaires["rnd"] = salaires.apply (lambda r : random.randint(0,50),axis=1)
ech = salaires [ salaires.rnd == 0 ]
X,Y = ech[["AGE","SEXE","TYP_EMPLOI","CONT_TRAV", "CS"]], ech[["montant"]]
Xd = X.T.to_dict().values()
from sklearn.feature_extraction import DictVectorizer
prep = DictVectorizer()
Xt = prep.fit_transform(Xd).toarray()
from sklearn.model_selection import train_test_split
a_train, a_test, b_train, b_test = train_test_split(Xt, Y, test_size=0.33)
from sklearn.ensemble import RandomForestRegressor
import matplotlib.pyplot as plt
from sklearn.metrics import mean_squared_error
from numpy import array
curves = []
for n_estimators in range(1,10) :
clf = RandomForestRegressor(n_estimators=n_estimators,max_depth=1,min_samples_leaf=10)
clf = clf.fit(a_train, b_train["montant"].ravel())
erra = mean_squared_error( clf.predict(a_train), b_train)**0.5
errb = mean_squared_error( clf.predict(a_test), b_test)**0.5
print("n_estimators",n_estimators, "erreur",erra,errb)
curves.append((n_estimators, erra,errb, clf) )
plt.plot ( [c[0] for c in curves], [c[1] for c in curves], label="train")
plt.plot ( [c[0] for c in curves], [c[2] for c in curves], label="test")
#plt.ylim( [11300,11600] )
plt.legend();
n_estimators 1 erreur 10777.861048518538 10774.134728955933
n_estimators 2 erreur 10724.224251649079 10730.920886589629
n_estimators 3 erreur 10777.677483141808 10774.12073998104
n_estimators 4 erreur 10752.485926963609 10754.003026467124
n_estimators 5 erreur 10745.185493268404 10749.020102424705
n_estimators 6 erreur 10734.423374628881 10738.124428332068
n_estimators 7 erreur 10761.323875241487 10760.754193848868
n_estimators 8 erreur 10777.633163165317 10774.12890244675
n_estimators 9 erreur 10733.20327466252 10735.903647029647
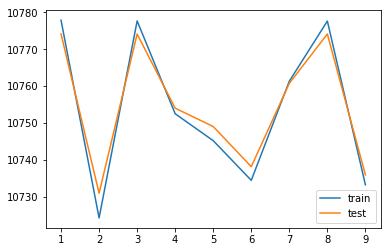
On obtient plus rapidement le même résultat qu’avec les arbres de décision.
Exercice 2 : Courbes ROC#
Première courbe#
On enlève juste les valeurs imprévues.
import random, numpy
tsalaires = salaires[ (salaires["SEXE"].notnull()) & ((salaires["SEXE"] == "1") | (salaires["SEXE"] == "2")) ].copy()
tsalaires["rnd"] = tsalaires.apply (lambda r : random.randint(0,50),axis=1)
ech = tsalaires [ tsalaires.rnd == 0 ].copy()
X,Y = ech[["AGE","TYP_EMPLOI","CONT_TRAV", "CS", "montant"]], ech[["SEXE"]].copy()
Xd = X.T.to_dict().values()
Y["SEXE"] = Y.apply ( lambda r : int(r["SEXE"])-1, axis=1)
from sklearn.feature_extraction import DictVectorizer
prep = DictVectorizer()
Xt = prep.fit_transform(Xd).toarray()
from sklearn.model_selection import train_test_split
a_train, a_test, b_train, b_test = train_test_split(Xt, Y, test_size=0.33)
On apprend un classifieur (masculin ou féminin) :
from sklearn.tree import DecisionTreeClassifier
clf = DecisionTreeClassifier(max_depth=10)
clf = clf.fit(a_train, b_train["SEXE"].ravel())
Et la courbe ROC :
from sklearn.metrics import roc_curve, auc
probas = clf.predict_proba(a_test)
# probas est une matrice de deux colonnes avec la proabilités d'appartenance à chaque classe
fpr, tpr, thresholds = roc_curve(b_test["SEXE"].ravel(), probas[:, 1])
roc_auc = auc(fpr, tpr)
print("Area under the ROC curve : %f" % roc_auc)
plt.plot(fpr, tpr, label='ROC curve (area = %0.2f)' % roc_auc)
plt.plot([0, 1], [0, 1], 'k--')
plt.xlim([0.0, 1.0])
plt.ylim([0.0, 1.0])
plt.xlabel('False Positive Rate')
plt.ylabel('True Positive Rate')
plt.title('Receiver operating characteristic example')
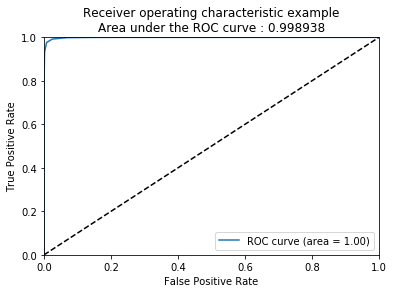
plt.legend(loc="lower right");
Area under the ROC curve : 0.780799
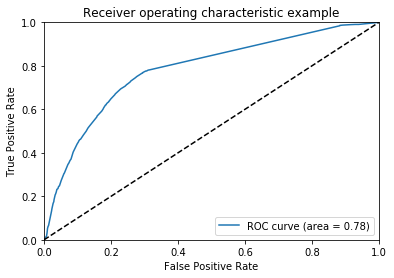
Une courbe comme celle-là veut dire que le classifieur ne fait pas beaucoup mieux que le hasard. On va tricher un peu et apprendre le modèle sur la base de test pour voir ce qu’on devrait voir si le modèle était un bon prédicteur :
from sklearn.ensemble import RandomForestClassifier
clf = RandomForestClassifier(n_estimators=10)
clf = clf.fit(a_test, b_test["SEXE"].ravel())
probas = clf.predict_proba(a_test)
# probas est une matrice de deux colonnes avec la proabilités d'appartenance à chaque classe
fpr, tpr, thresholds = roc_curve(b_test["SEXE"].ravel(), probas[:, 1])
roc_auc = auc(fpr, tpr)
plt.plot(fpr, tpr, label='ROC curve (area = %0.2f)' % roc_auc)
plt.plot([0, 1], [0, 1], 'k--')
plt.xlim([0.0, 1.0])
plt.ylim([0.0, 1.0])
plt.xlabel('False Positive Rate')
plt.ylabel('True Positive Rate')
plt.title('Receiver operating characteristic example\nArea under the ROC curve : %f' % roc_auc)
plt.legend(loc="lower right");
Un peu plus de features et…#
Dans les exemples précédents, deux variables numériques (AGE et
montant) ont été traitées comme catégorielles et il serait plus
efficace de les traiter comme numériques (1 feature au lieu
features avec
= le nombre d’âges différents). Cela présente
l’avantage de ne pas avoir que des features
sparses.
import random, numpy
tsalaires = salaires[ (salaires["SEXE"].notnull()) & ((salaires["SEXE"] == "1") | (salaires["SEXE"] == "2")) ].copy()
tsalaires["rnd"] = tsalaires.apply (lambda r : random.randint(0,50),axis=1)
ech = tsalaires [ tsalaires.rnd == 0 ].copy()
Xn,Xc,Y = ech[["AGE","montant"]], \
ech[["TYP_EMPLOI","CONT_TRAV", "CS", "CONV_COLL", "DEPT", "DEPR", "PCS"]], \
ech[["SEXE"]].copy()
Xd = Xc.T.to_dict().values()
Y["SEXE"] = Y.apply ( lambda r : int(r["SEXE"])-1, axis=1)
from sklearn.feature_extraction import DictVectorizer
prep = DictVectorizer()
Xt = prep.fit_transform(Xd).toarray()
Xt = numpy.hstack((Xn,Xt))
from sklearn.model_selection import train_test_split
a_train, a_test, b_train, b_test = train_test_split(Xt, Y, test_size=0.33)
On teste différents modèles et on vérifie que le fait de considérer les
variables AGE et montant est plus efficace. Les deux dernières
options proposent deux façons de réduire le nombre de varaibles en
entrée avec une ACP et en utilisant un objet
Pipeline
qui permet de chaîner les opérations sur le même jeu de données. Ce
dernière exemple explique l’intérêt d’avoir les mêmes méthodes pour
chaque modèle.
model = "GBC"
if model == "lda":
from sklearn.discriminant_analysis import LinearDiscriminantAnalysis
clf = LinearDiscriminantAnalysis(n_components=2)
clf = clf.fit(a_train, (b_train["SEXE"]+1.0).ravel())
elif model == "tree":
from sklearn.tree import DecisionTreeClassifier
clf = DecisionTreeClassifier(max_depth=10)
clf = clf.fit(a_train, b_train["SEXE"].ravel())
elif model == "forest":
from sklearn.ensemble import RandomForestClassifier
clf = RandomForestClassifier()
clf = clf.fit(a_train, b_train["SEXE"].ravel())
elif model=="pipeline":
from sklearn.pipeline import Pipeline
from sklearn.svm import LinearSVC
from sklearn.decomposition import PCA
from sklearn.discriminant_analysis import LinearDiscriminantAnalysis
clf = Pipeline([
('feature_selection', PCA(n_components=10)),
('classification', LinearDiscriminantAnalysis())
])
clf = clf.fit(a_train, b_train["SEXE"].ravel())
elif model=="GBC":
from sklearn.ensemble import GradientBoostingClassifier
clf = GradientBoostingClassifier(n_estimators=10)
clf = clf.fit(a_train, b_train["SEXE"].ravel())
else:
raise Exception("unknown model: " + model)
On trace la courbe ROC pour mesurer la performance du modèle.
from sklearn.metrics import roc_curve, auc
probas = clf.predict_proba(a_test)
fpr, tpr, thresholds = roc_curve(b_test["SEXE"].ravel(), probas[:, 1])
roc_auc = auc(fpr, tpr)
plt.plot(fpr, tpr, label='ROC curve (area = %0.2f)' % roc_auc)
plt.plot([0, 1], [0, 1], 'k--')
plt.xlim([0.0, 1.0])
plt.ylim([0.0, 1.0])
plt.xlabel('False Positive Rate')
plt.ylabel('True Positive Rate')
plt.title('ROC ' + model + '\n' + "Area under the ROC curve : %f" % roc_auc)
plt.legend(loc="lower right");
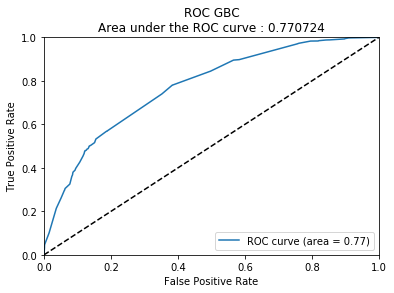
Si le model choisi est un GradientBoostingClassifier, on peut regarder l’importance des variables dans la construction du résultat. Le graphe suivant est inspiré de la page Gradient Boosting regression même si ce n’est pas une régression qui a été utilisée ici.
if model == "GBC":
import pandas
import numpy as np
feature_name = pandas.Series(["AGE","montant"] + prep.feature_names_)
limit = 20
feature_importance = clf.feature_importances_[:20]
feature_importance = 100.0 * (feature_importance / feature_importance.max())
sorted_idx = np.argsort(feature_importance)
pos = np.arange(sorted_idx.shape[0]) + .5
plt.subplot(1, 2, 2)
plt.barh(pos, feature_importance[sorted_idx], align='center')
plt.yticks(pos, feature_name[sorted_idx])
plt.xlabel('Relative Importance')
plt.title('Variable Importance');
