2A.ml - 2016 - Compétition - Préparation des données#
Links: notebook, html, python, slides, GitHub
Une compétition était proposée dans le cadre du cours Python pour un Data Scientist à l’ENSAE. Ce notebook facilite la prise en main des données et montre comment comparer plusieurs classifieurs avec la courbe ROC.
from jyquickhelper import add_notebook_menu
add_notebook_menu()
The history saving thread hit an unexpected error (OperationalError('database is locked',)).History will not be written to the database.
from pyensae.datasource import download_data
download_data("ensae_competition_2016.zip",
url="https://github.com/sdpython/ensae_teaching_cs/raw/master/_doc/competitions/2016_ENSAE_2A/")
['ensae_competition_test_X.txt', 'ensae_competition_train.txt']
%matplotlib inline
Données#
import pandas as p
import numpy as np
df = p.read_csv('./ensae_competition_train.txt', header=[0,1], sep="\t", index_col=0)
#### Gender dummies
df['X2'] = df['X2'].applymap(str)
gender_dummies = p.get_dummies(df['X2'] )
### education dummies
df['X3'] = df['X3'].applymap(str)
educ_dummies = p.get_dummies(df['X3'] )
#### marriage dummies
df['X4'] = df['X4'].applymap(str)
mariage_dummies = p.get_dummies(df['X4'] )
### On va aussi supprimer les multi index de la table
df.columns = df.columns.droplevel(0)
#### on aggrège ensuite les 3 tables ensemble
data = df.join(gender_dummies).join(educ_dummies).join(mariage_dummies)
data.rename(columns = {'default payment next month' : "Y"}, inplace = True)
data = data.drop(['SEX','EDUCATION','MARRIAGE'],1)
data_resample = p.concat([data[data['Y']==1], data[data['Y']==0].sample(len(data[data['Y']==1]))])
data.head(n=2)
| LIMIT_BAL | AGE | PAY_0 | PAY_2 | PAY_3 | PAY_4 | PAY_5 | PAY_6 | BILL_AMT1 | BILL_AMT2 | ... | EDUCATION_1 | EDUCATION_2 | EDUCATION_3 | EDUCATION_4 | EDUCATION_5 | EDUCATION_6 | MARRIAGE_0 | MARRIAGE_1 | MARRIAGE_2 | MARRIAGE_3 | |
|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|
| 0 | 180000 | 47 | 0 | 0 | 0 | 0 | 0 | 0 | 179253 | 95170 | ... | 0 | 1 | 0 | 0 | 0 | 0 | 0 | 1 | 0 | 0 |
| 1 | 110000 | 35 | 0 | 0 | 0 | 0 | 0 | 0 | 6137 | 7040 | ... | 0 | 1 | 0 | 0 | 0 | 0 | 0 | 1 | 0 | 0 |
2 rows × 34 columns
Y = data['Y']
Y = data_resample['Y']
X = data.drop('Y', 1)
#X = data[["SEX_1", "AGE", "MARRIAGE_0", 'PAY_0']]
X = data_resample.drop('Y',1)
X.columns
Index(['LIMIT_BAL', 'AGE', 'PAY_0', 'PAY_2', 'PAY_3', 'PAY_4', 'PAY_5',
'PAY_6', 'BILL_AMT1', 'BILL_AMT2', 'BILL_AMT3', 'BILL_AMT4',
'BILL_AMT5', 'BILL_AMT6', 'PAY_AMT1', 'PAY_AMT2', 'PAY_AMT3',
'PAY_AMT4', 'PAY_AMT5', 'PAY_AMT6', 'SEX_1', 'SEX_2', 'EDUCATION_0',
'EDUCATION_1', 'EDUCATION_2', 'EDUCATION_3', 'EDUCATION_4',
'EDUCATION_5', 'EDUCATION_6', 'MARRIAGE_0', 'MARRIAGE_1', 'MARRIAGE_2',
'MARRIAGE_3'],
dtype='object')
from sklearn.model_selection import train_test_split
X_train, X_test, Y_train, Y_test = train_test_split(X, Y, test_size=0.33)
Choix du Classifieur#
from sklearn.linear_model import LogisticRegression
from sklearn import svm
from sklearn.ensemble import GradientBoostingClassifier, RandomForestClassifier
from sklearn.linear_model import SGDClassifier, Perceptron
#type_classifier = LogisticRegression
#type_classifier = svm.SVC
type_classifier = GradientBoostingClassifier
#type_classifier = RandomForestClassifier
#type_classifier = Perceptron
clf = type_classifier()
#clf = SGDClassifier(loss="hinge", penalty="l2")
clf = clf.fit(X_train, Y_train.ravel())
# Matrice de confusion
%matplotlib inline
from sklearn.metrics import confusion_matrix
for x,y in [ (X_train, Y_train), (X_test, Y_test) ]:
yp = clf.predict(x)
cm = confusion_matrix(y.ravel(), yp.ravel())
print(cm.transpose())
import matplotlib.pyplot as plt
import seaborn as sns
sns.set_style('ticks')
plt.matshow(cm.transpose())
plt.title('Confusion matrix sur Test')
plt.colorbar()
plt.ylabel('Predicted label')
plt.xlabel('True label')
[[2713 1112]
[ 641 2207]]
[[1272 590]
[ 354 1071]]
<matplotlib.text.Text at 0x253d132cd68>
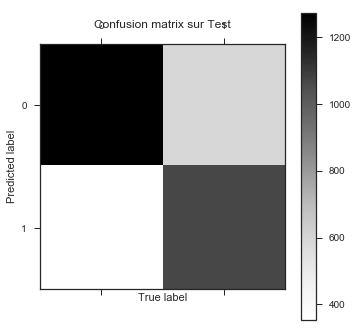
(cm.transpose()[0,0]+cm.transpose()[1,1])/ (cm[0].sum()+cm[1].sum())
0.71280803163979312
Calcul du critère AUC#
from sklearn.metrics import roc_curve, auc
probas = clf.predict_proba(X_test)
probas
array([[ 0.14376934, 0.85623066],
[ 0.78068073, 0.21931927],
[ 0.76203158, 0.23796842],
...,
[ 0.36898867, 0.63101133],
[ 0.45767261, 0.54232739],
[ 0.21353388, 0.78646612]])
rep = [ ]
yt = Y_test.ravel()
for i in range(probas.shape[0]):
p0,p1 = probas[i,:]
exp = yt[i]
if p0 > p1 :
if exp == 0 :
# bonne réponse, true positive (tp)
rep.append ( (1, p0) )
else :
# mauvaise réponse, false positive (fp)
rep.append( (0, p0) )
else :
if exp == 0 :
# mauvaise réponse, false negative (fn)
rep.append ( (0, p1) )
else :
# bonne réponse, true negative (tn)
rep.append( (1, p1) )
mat_rep = np.array(rep)
print("AUC : Taux de bonnes réponses" , sum(mat_rep[:,0]) / len(mat_rep[:,0]))
AUC : Taux de bonnes réponses 0.71280803164
Tous les critères sont détaillés là. Attention au sens de la matrice de confusion, selon les articles, cela change.
Courbe ROC#
fpr, tpr, thresholds = roc_curve(mat_rep[:,0], mat_rep[:, 1])
roc_auc = auc(fpr, tpr)
plt.plot(fpr, tpr, label='ROC curve (area = %0.2f)' % roc_auc)
plt.plot([0, 1], [0, 1], 'k--')
plt.xlim([0.0, 1.0])
plt.ylim([0.0, 1.0])
plt.xlabel('False Positive Rate')
plt.ylabel('True Positive Rate (or precision)')
plt.title('ROC')
plt.legend(loc="lower right")
<matplotlib.legend.Legend at 0x253d2608ef0>
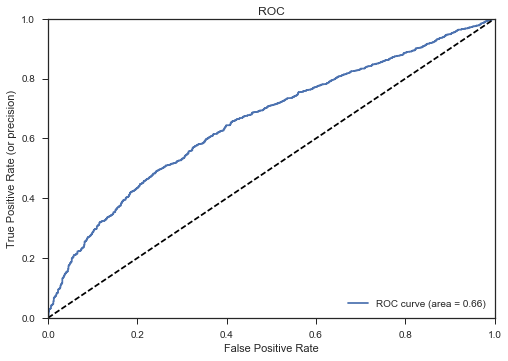
En haut à droite, TPR et FPR valent 1 (il suffit de prédire toujours positif = pas de défaut = Y_hat=0), en bas à gauche, TPR et FPR valent 0 parce qu’il suffit de toujours prédire la situation négative (ou le défaut, Y_hat = 1).
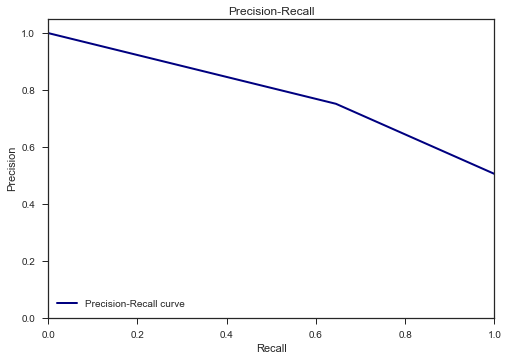
Une autre métrique souvent suivie consiste à comparer Precision (= TPR) et Recall. C’est un peu le même arbitrage. Cela devrait vous rappeler celui entre risque de première espèce et puissance d’un test.
Précision-Recall, Score F1#
tp=0
fp=0
fn=0
tn=0
for i in range(len(probas[:,0])):
if (probas[i,0] >= 0.5 and yt[i] == 0):
tp+=1
elif (probas[i,0] >= 0.5 and yt[i] == 1):
fp+=1
elif (probas[i,0] <= 0.5 and yt[i] == 0):
fn+=1
else:
tn+=1
print("On retrouve la matrice de confusion :\n", "TP : ", tp, "FP : ", fp, "\n",
" FN : ", fn, "TN : ", tn)
print("Precision : TP / (TP + FP) = ", tp/(tp+fp))
print("Recall : TP / (TP + FN) = ", tp/(tp+fn))
precision = tp/(tp+fp)
recall = tp/(tp+fn)
print("F1 Score : T2 * P * R / (P + R) = ", 2 * precision * recall / (precision + recall) )
print("False Positive rate : FP / (FP + FN) = ", fp/(fp+tn))
On retrouve la matrice de confusion :
TP : 1272 FP : 590
FN : 354 TN : 1071
Precision : TP / (TP + FP) = 0.6831364124597207
Recall : TP / (TP + FN) = 0.7822878228782287
F1 Score : T2 * P * R / (P + R) = 0.7293577981651376
False Positive rate : FP / (FP + FN) = 0.35520770620108366
from sklearn.metrics import precision_recall_curve
precision, recall, _ = precision_recall_curve(Y_test.ravel(), yp.ravel())
lw = 2
plt.plot(recall, precision, lw=lw, color='navy', label='Precision-Recall curve')
plt.xlabel('Recall')
plt.ylabel('Precision')
plt.ylim([0.0, 1.05])
plt.xlim([0.0, 1.0])
plt.title('Precision-Recall')
plt.legend(loc="lower left")
<matplotlib.legend.Legend at 0x253d268c908>