2A.ml - 2016 - Compétition - Importation des données#
Links: notebook, html, python, slides, GitHub
Une compétition était proposée dans le cadre du cours Python pour un Data Scientist à l’ENSAE. Ce notebook facilite la prise en main des données et étudie les données avec des méthodes de statistiques descriptives.
%matplotlib inline
from jyquickhelper import add_notebook_menu
add_notebook_menu()
from pyensae.datasource import download_data
download_data("ensae_competition_2016.zip",
url="https://github.com/sdpython/ensae_teaching_cs/raw/master/_doc/competitions/2016_ENSAE_2A/")
['ensae_competition_test_X.txt', 'ensae_competition_train.txt']
Données#
import pandas as p
df = p.read_csv('./ensae_competition_train.txt', header=[0,1], sep="\t", index_col=0)
df.head()
| X1 | X2 | X3 | X4 | X5 | X6 | X7 | X8 | X9 | X10 | ... | X15 | X16 | X17 | X18 | X19 | X20 | X21 | X22 | X23 | Y | |
|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|
| ID | LIMIT_BAL | SEX | EDUCATION | MARRIAGE | AGE | PAY_0 | PAY_2 | PAY_3 | PAY_4 | PAY_5 | ... | BILL_AMT4 | BILL_AMT5 | BILL_AMT6 | PAY_AMT1 | PAY_AMT2 | PAY_AMT3 | PAY_AMT4 | PAY_AMT5 | PAY_AMT6 | default payment next month |
| 0 | 180000 | 1 | 2 | 1 | 47 | 0 | 0 | 0 | 0 | 0 | ... | 99694 | 65977 | 67415 | 3700 | 3700 | 4100 | 2360 | 2500 | 2618 | 0 |
| 1 | 110000 | 2 | 2 | 1 | 35 | 0 | 0 | 0 | 0 | 0 | ... | 4869 | 4966 | 5070 | 1053 | 1073 | 1081 | 178 | 184 | 185 | 1 |
| 2 | 70000 | 2 | 2 | 2 | 22 | 0 | 0 | 0 | 0 | 0 | ... | 69927 | 50579 | 49483 | 2501 | 3001 | 2608 | 1777 | 1792 | 1793 | 1 |
| 3 | 200000 | 2 | 1 | 2 | 27 | -2 | -2 | -2 | -2 | -2 | ... | 1665 | 3370 | -36 | 5610 | 15616 | 1673 | 3385 | 0 | 95456 | 0 |
| 4 | 370000 | 2 | 1 | 1 | 39 | 0 | 0 | 0 | 0 | 0 | ... | 48216 | 47675 | 48074 | 2157 | 2000 | 1668 | 2000 | 3000 | 1000 | 0 |
5 rows × 24 columns
len(df)
22500
This research employed a binary variable, default payment (Yes = 1, No = 0), as the response variable. This study reviewed the literature and used the following 23 variables as explanatory variables: - X1: Amount of the given credit (NT dollar): it includes both the individual consumer credit and his/her family (supplementary) credit. - X2: Gender (1 = male; 2 = female). - X3: Education (1 = graduate school; 2 = university; 3 = high school; 4 = others). - X4: Marital status (1 = married; 2 = single; 3 = others). - X5: Age (year). - X6 - X11: History of past payment. We tracked the past monthly payment records (from April to September, 2005) as follows: X6 = the repayment status in September, 2005; X7 = the repayment status in August, 2005; …;X11 = the repayment status in April, 2005. The measurement scale for the repayment status is: -1 = pay duly; 1 = payment delay for one month; 2 = payment delay for two months; …; 8 = payment delay for eight months; 9 = payment delay for nine months and above. - X12-X17: Amount of bill statement (NT dollar). X12 = amount of bill statement in September, 2005; X13 = amount of bill statement in August, 2005; …; X17 = amount of bill statement in April, 2005. - X18-X23: Amount of previous payment (NT dollar). X18 = amount paid in September, 2005; X19 = amount paid in August, 2005; …;X23 = amount paid in April, 2005.
#Format des variables : multiindex
print(df[('Y','default payment next month')].value_counts())
print(df['Y']['default payment next month'].value_counts())
0 17520
1 4980
Name: (Y, default payment next month), dtype: int64
0 17520
1 4980
Name: default payment next month, dtype: int64
df.columns = df.columns.droplevel()
df.rename(columns={'default payment next month':'Y'},inplace=True)
df.head()
| ID | LIMIT_BAL | SEX | EDUCATION | MARRIAGE | AGE | PAY_0 | PAY_2 | PAY_3 | PAY_4 | PAY_5 | ... | BILL_AMT4 | BILL_AMT5 | BILL_AMT6 | PAY_AMT1 | PAY_AMT2 | PAY_AMT3 | PAY_AMT4 | PAY_AMT5 | PAY_AMT6 | Y |
|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|
| 0 | 180000 | 1 | 2 | 1 | 47 | 0 | 0 | 0 | 0 | 0 | ... | 99694 | 65977 | 67415 | 3700 | 3700 | 4100 | 2360 | 2500 | 2618 | 0 |
| 1 | 110000 | 2 | 2 | 1 | 35 | 0 | 0 | 0 | 0 | 0 | ... | 4869 | 4966 | 5070 | 1053 | 1073 | 1081 | 178 | 184 | 185 | 1 |
| 2 | 70000 | 2 | 2 | 2 | 22 | 0 | 0 | 0 | 0 | 0 | ... | 69927 | 50579 | 49483 | 2501 | 3001 | 2608 | 1777 | 1792 | 1793 | 1 |
| 3 | 200000 | 2 | 1 | 2 | 27 | -2 | -2 | -2 | -2 | -2 | ... | 1665 | 3370 | -36 | 5610 | 15616 | 1673 | 3385 | 0 | 95456 | 0 |
| 4 | 370000 | 2 | 1 | 1 | 39 | 0 | 0 | 0 | 0 | 0 | ... | 48216 | 47675 | 48074 | 2157 | 2000 | 1668 | 2000 | 3000 | 1000 | 0 |
5 rows × 24 columns
Distinction des variables catégorielles#
df.columns
Index(['LIMIT_BAL', 'SEX', 'EDUCATION', 'MARRIAGE', 'AGE', 'PAY_0', 'PAY_2',
'PAY_3', 'PAY_4', 'PAY_5', 'PAY_6', 'BILL_AMT1', 'BILL_AMT2',
'BILL_AMT3', 'BILL_AMT4', 'BILL_AMT5', 'BILL_AMT6', 'PAY_AMT1',
'PAY_AMT2', 'PAY_AMT3', 'PAY_AMT4', 'PAY_AMT5', 'PAY_AMT6', 'Y'],
dtype='object', name='ID')
cat_var = list(df.columns[1:4]) + list(df.columns[5:11]) + list(df.columns[-1:])
num_var = [v for v in df.columns if v not in cat_var]
print("Categorical variables: ", cat_var)
print("Numerical variables: " , num_var)
for v in cat_var[:-1]:
df[v]=p.DataFrame(df[v]).applymap(str)
Categorical variables: ['SEX', 'EDUCATION', 'MARRIAGE', 'PAY_0', 'PAY_2', 'PAY_3', 'PAY_4', 'PAY_5', 'PAY_6', 'Y']
Numerical variables: ['LIMIT_BAL', 'AGE', 'BILL_AMT1', 'BILL_AMT2', 'BILL_AMT3', 'BILL_AMT4', 'BILL_AMT5', 'BILL_AMT6', 'PAY_AMT1', 'PAY_AMT2', 'PAY_AMT3', 'PAY_AMT4', 'PAY_AMT5', 'PAY_AMT6']
num_var_bill = [ v for v in num_var if 'BILL' in v or v == 'LIMIT_BAL']
num_var_pay = [ v for v in num_var if 'PAY' in v ]
print("Numerical variables BILL: ", num_var_bill)
print("Numerical variables PAY: " , num_var_pay)
Numerical variables BILL: ['LIMIT_BAL', 'BILL_AMT1', 'BILL_AMT2', 'BILL_AMT3', 'BILL_AMT4', 'BILL_AMT5', 'BILL_AMT6']
Numerical variables PAY: ['PAY_AMT1', 'PAY_AMT2', 'PAY_AMT3', 'PAY_AMT4', 'PAY_AMT5', 'PAY_AMT6']
Variable d’intérêt#
default=df[df['Y']==1]
solvent=df[df['Y']==0]
df['Y'].value_counts()
0 17520
1 4980
Name: Y, dtype: int64
Statistiques Descriptives#
Variables quantitatives#
desc=df[num_var].describe()
std=p.DataFrame(df[num_var].std()).transpose()
std.rename(index={0:'std'},inplace=True)
res=p.concat([desc,std])
res
| ID | LIMIT_BAL | AGE | BILL_AMT1 | BILL_AMT2 | BILL_AMT3 | BILL_AMT4 | BILL_AMT5 | BILL_AMT6 | PAY_AMT1 | PAY_AMT2 | PAY_AMT3 | PAY_AMT4 | PAY_AMT5 | PAY_AMT6 |
|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|
| count | 22500.000000 | 22500.000000 | 22500.000000 | 22500.000000 | 2.250000e+04 | 22500.000000 | 22500.000000 | 22500.000000 | 22500.000000 | 2.250000e+04 | 22500.000000 | 22500.000000 | 22500.000000 | 22500.000000 |
| mean | 167031.985778 | 35.522622 | 51377.476533 | 49254.855378 | 4.719780e+04 | 43390.913156 | 40370.602000 | 38961.910489 | 5573.344400 | 5.981831e+03 | 5159.924000 | 4783.836400 | 4761.467022 | 5319.834311 |
| std | 129410.412959 | 9.240719 | 73518.931398 | 70946.251776 | 6.954210e+04 | 64346.612034 | 60746.789532 | 59597.874685 | 15467.825328 | 2.282096e+04 | 16085.885024 | 15626.493539 | 15349.550859 | 18196.730565 |
| min | 10000.000000 | 21.000000 | -165580.000000 | -67526.000000 | -1.572640e+05 | -170000.000000 | -81334.000000 | -339603.000000 | 0.000000 | 0.000000e+00 | 0.000000 | 0.000000 | 0.000000 | 0.000000 |
| 25% | 50000.000000 | 28.000000 | 3565.000000 | 3069.250000 | 2.740000e+03 | 2350.000000 | 1763.000000 | 1253.750000 | 1000.000000 | 8.750000e+02 | 396.000000 | 300.000000 | 250.000000 | 154.000000 |
| 50% | 140000.000000 | 34.000000 | 22578.500000 | 21365.500000 | 2.020250e+04 | 19095.500000 | 18104.500000 | 17125.000000 | 2100.000000 | 2.009000e+03 | 1800.000000 | 1500.000000 | 1500.000000 | 1500.000000 |
| 75% | 240000.000000 | 41.000000 | 67254.750000 | 64252.750000 | 6.019275e+04 | 54475.000000 | 50090.250000 | 49063.250000 | 5006.000000 | 5.000000e+03 | 4500.000000 | 4000.000000 | 4013.250000 | 4005.000000 |
| max | 800000.000000 | 79.000000 | 746814.000000 | 743970.000000 | 1.664089e+06 | 628699.000000 | 823540.000000 | 699944.000000 | 505000.000000 | 1.684259e+06 | 508229.000000 | 528897.000000 | 426529.000000 | 527143.000000 |
| std | 129410.412959 | 9.240719 | 73518.931398 | 70946.251776 | 6.954210e+04 | 64346.612034 | 60746.789532 | 59597.874685 | 15467.825328 | 2.282096e+04 | 16085.885024 | 15626.493539 | 15349.550859 | 18196.730565 |
from pandas import DataFrame
import matplotlib.pyplot as plt
import seaborn as sns
# from seaborn.timeseries import tsplot as tsplot
from seaborn import lineplot as tsplot
import numpy as np
fig = plt.figure(figsize=(20,10))
ax1 = fig.add_subplot(121)
ax2 = fig.add_subplot(122)
sns.set(style="ticks")
ax1.set_ylim([15000,25000])
ax2.set_ylim([1000,2500])
ax1.set_title('BILL variables',fontsize=14)
ax2.set_title('PAY variables',fontsize=14)
df_bill = DataFrame(data=df[num_var_bill[1:]].values.ravel(), columns=['bill'])
df_bill['index'] = [(i % 6 + 1) for i in range(df_bill.shape[0])]
tsplot(x='index', y='bill',
estimator=np.median, ax=ax1, data=df_bill)
df_pay = DataFrame(data=df[num_var_pay].values.ravel(), columns=['pay'])
df_pay['index'] = [(i % 6 + 1) for i in range(df_bill.shape[0])]
tsplot(x='index', y='pay',
estimator=np.median, ax=ax2, data=df_pay);

desc=default[num_var].describe()
std=p.DataFrame(default[num_var].std()).transpose()
std.rename(index={0:'std'},inplace=True)
p.concat([desc,std])
| ID | LIMIT_BAL | AGE | BILL_AMT1 | BILL_AMT2 | BILL_AMT3 | BILL_AMT4 | BILL_AMT5 | BILL_AMT6 | PAY_AMT1 | PAY_AMT2 | PAY_AMT3 | PAY_AMT4 | PAY_AMT5 | PAY_AMT6 |
|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|
| count | 4980.000000 | 4980.000000 | 4980.000000 | 4980.000000 | 4980.000000 | 4980.000000 | 4980.000000 | 4980.000000 | 4980.000000 | 4980.000000 | 4980.000000 | 4980.000000 | 4980.00000 | 4980.000000 |
| mean | 128369.012048 | 35.898594 | 48802.007430 | 47508.621486 | 45354.507631 | 42269.960040 | 39794.054418 | 38482.410843 | 3235.062450 | 3389.897992 | 3449.471888 | 3089.322490 | 3048.47751 | 3508.093173 |
| std | 114585.300619 | 9.785178 | 73208.224739 | 70957.968104 | 68145.557400 | 64232.730366 | 61745.867002 | 59804.195524 | 7333.004363 | 11169.855676 | 13776.576790 | 10998.148448 | 10471.88080 | 13996.188125 |
| min | 10000.000000 | 21.000000 | -6676.000000 | -17710.000000 | -61506.000000 | -65167.000000 | -53007.000000 | -339603.000000 | 0.000000 | 0.000000 | 0.000000 | 0.000000 | 0.00000 | 0.000000 |
| 25% | 50000.000000 | 28.000000 | 3351.750000 | 3099.750000 | 2574.250000 | 2302.500000 | 1475.250000 | 1168.250000 | 0.000000 | 0.000000 | 0.000000 | 0.000000 | 0.00000 | 0.000000 |
| 50% | 90000.000000 | 34.000000 | 20738.500000 | 20715.000000 | 20105.000000 | 19344.500000 | 18661.000000 | 18254.000000 | 1642.500000 | 1573.000000 | 1242.500000 | 1000.000000 | 1000.00000 | 1000.000000 |
| 75% | 190000.000000 | 42.000000 | 59812.250000 | 58135.250000 | 54888.750000 | 50483.250000 | 48421.250000 | 47740.750000 | 3435.250000 | 3321.000000 | 3000.000000 | 2902.500000 | 3000.00000 | 2935.500000 |
| max | 720000.000000 | 75.000000 | 613860.000000 | 581775.000000 | 578971.000000 | 548020.000000 | 547880.000000 | 514975.000000 | 175100.000000 | 344467.000000 | 508229.000000 | 432130.000000 | 332000.00000 | 345293.000000 |
| std | 114585.300619 | 9.785178 | 73208.224739 | 70957.968104 | 68145.557400 | 64232.730366 | 61745.867002 | 59804.195524 | 7333.004363 | 11169.855676 | 13776.576790 | 10998.148448 | 10471.88080 | 13996.188125 |
desc=solvent[num_var].describe()
std=p.DataFrame(solvent[num_var].std()).transpose()
std.rename(index={0:'std'},inplace=True)
p.concat([desc,std])
| ID | LIMIT_BAL | AGE | BILL_AMT1 | BILL_AMT2 | BILL_AMT3 | BILL_AMT4 | BILL_AMT5 | BILL_AMT6 | PAY_AMT1 | PAY_AMT2 | PAY_AMT3 | PAY_AMT4 | PAY_AMT5 | PAY_AMT6 |
|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|
| count | 17520.000000 | 17520.000000 | 17520.000000 | 17520.000000 | 1.752000e+04 | 17520.000000 | 17520.000000 | 17520.000000 | 17520.000000 | 1.752000e+04 | 17520.000000 | 17520.000000 | 17520.000000 | 17520.000000 |
| mean | 178021.803653 | 35.415753 | 52109.544806 | 49751.216381 | 4.772175e+04 | 43709.540240 | 40534.483676 | 39098.206621 | 6237.993037 | 6.718579e+03 | 5646.114155 | 5265.496176 | 5248.378425 | 5834.815525 |
| std | 131264.434306 | 9.077451 | 73592.642301 | 70937.100523 | 6.992702e+04 | 64377.214009 | 60460.571694 | 59540.104394 | 17028.973430 | 2.511828e+04 | 16652.378496 | 16678.582519 | 16442.208028 | 19193.074508 |
| min | 10000.000000 | 21.000000 | -165580.000000 | -67526.000000 | -1.572640e+05 | -170000.000000 | -81334.000000 | -150953.000000 | 0.000000 | 0.000000e+00 | 0.000000 | 0.000000 | 0.000000 | 0.000000 |
| 25% | 70000.000000 | 28.000000 | 3610.750000 | 3059.750000 | 2.774000e+03 | 2368.500000 | 1830.500000 | 1261.000000 | 1170.000000 | 1.010750e+03 | 600.000000 | 390.000000 | 359.000000 | 323.000000 |
| 50% | 150000.000000 | 34.000000 | 23100.500000 | 21571.500000 | 2.021500e+04 | 18983.000000 | 17919.500000 | 16677.500000 | 2440.000000 | 2.244500e+03 | 2000.000000 | 1732.500000 | 1738.500000 | 1738.000000 |
| 75% | 250000.000000 | 41.000000 | 69197.750000 | 66165.000000 | 6.214250e+04 | 55812.750000 | 51010.750000 | 49667.500000 | 5600.250000 | 5.363000e+03 | 5000.000000 | 4580.000000 | 4600.000000 | 4600.000000 |
| max | 800000.000000 | 79.000000 | 746814.000000 | 743970.000000 | 1.664089e+06 | 628699.000000 | 823540.000000 | 699944.000000 | 505000.000000 | 1.684259e+06 | 417588.000000 | 528897.000000 | 426529.000000 | 527143.000000 |
| std | 131264.434306 | 9.077451 | 73592.642301 | 70937.100523 | 6.992702e+04 | 64377.214009 | 60460.571694 | 59540.104394 | 17028.973430 | 2.511828e+04 | 16652.378496 | 16678.582519 | 16442.208028 | 19193.074508 |
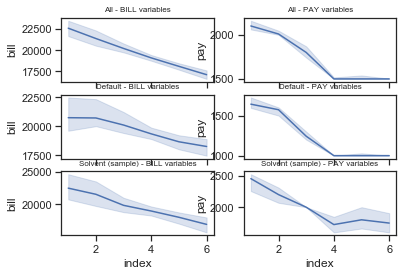
Biais de sélection sur les clients suceptibles de faire défaut ? Ou effet de taille (catégorie moins nombreuse) => moins de chances d’avoir des crédits élevés.
sample=solvent[num_var].sample(len(default))
desc=sample.describe()
std=p.DataFrame(sample.std()).transpose()
std.rename(index={0:'std'},inplace=True)
p.concat([desc,std])
| ID | LIMIT_BAL | AGE | BILL_AMT1 | BILL_AMT2 | BILL_AMT3 | BILL_AMT4 | BILL_AMT5 | BILL_AMT6 | PAY_AMT1 | PAY_AMT2 | PAY_AMT3 | PAY_AMT4 | PAY_AMT5 | PAY_AMT6 |
|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|
| count | 4980.000000 | 4980.000000 | 4980.000000 | 4980.000000 | 4.980000e+03 | 4980.000000 | 4980.000000 | 4980.000000 | 4980.000000 | 4.980000e+03 | 4980.000000 | 4980.000000 | 4980.000000 | 4980.000000 |
| mean | 178758.232932 | 35.390361 | 51695.869277 | 49837.375301 | 4.820321e+04 | 44399.457631 | 41018.500803 | 39998.024096 | 6512.932530 | 7.346733e+03 | 6015.037952 | 5586.750402 | 5495.629116 | 5726.194578 |
| std | 130737.258468 | 8.981527 | 73531.303800 | 71880.590268 | 7.402455e+04 | 66606.250803 | 62446.216266 | 61701.050046 | 17821.114507 | 3.596650e+04 | 18046.780932 | 18257.588434 | 17987.977867 | 18497.950374 |
| min | 10000.000000 | 21.000000 | -11545.000000 | -67526.000000 | -3.404100e+04 | -170000.000000 | -81334.000000 | -150953.000000 | 0.000000 | 0.000000e+00 | 0.000000 | 0.000000 | 0.000000 | 0.000000 |
| 25% | 70000.000000 | 28.000000 | 3522.500000 | 2956.250000 | 2.712000e+03 | 2428.500000 | 1749.750000 | 1201.500000 | 1200.000000 | 1.000000e+03 | 616.750000 | 389.000000 | 345.000000 | 300.000000 |
| 50% | 150000.000000 | 34.000000 | 22480.500000 | 21535.000000 | 1.984000e+04 | 18968.000000 | 18006.000000 | 16916.500000 | 2453.500000 | 2.200000e+03 | 2000.000000 | 1724.000000 | 1800.000000 | 1748.000000 |
| 75% | 250000.000000 | 41.000000 | 67147.250000 | 64884.500000 | 6.077775e+04 | 56010.250000 | 50914.750000 | 50060.250000 | 5785.500000 | 5.500000e+03 | 5000.000000 | 4487.750000 | 4770.250000 | 4686.250000 |
| max | 760000.000000 | 75.000000 | 621749.000000 | 597793.000000 | 1.664089e+06 | 616836.000000 | 823540.000000 | 568638.000000 | 493358.000000 | 1.684259e+06 | 417588.000000 | 497000.000000 | 417990.000000 | 443001.000000 |
| std | 130737.258468 | 8.981527 | 73531.303800 | 71880.590268 | 7.402455e+04 | 66606.250803 | 62446.216266 | 61701.050046 | 17821.114507 | 3.596650e+04 | 18046.780932 | 18257.588434 | 17987.977867 | 18497.950374 |
Il semble y avoir un biais de sélection en amont.
import matplotlib.pyplot as plt
import seaborn as sns
import numpy as np
fig, axes = plt.subplots(3,2, sharex=True)
fig = plt.figure(figsize=(20,10))
sns.set(style="ticks")
df_dict={0: 'All - ', 1 : 'Default - ' , 2 : 'Solvent (sample) - '}
var_dict={0: 'BILL variables', 1 : 'PAY variables'}
for i in range(3):
for j in range(2):
axes[i,j].set_title(df_dict[i] + var_dict[j],fontsize=8)
df_bill = DataFrame(data=df[num_var_bill[1:]].values.ravel(), columns=['bill'])
df_bill['index'] = [(i % 6 + 1) for i in range(df_bill.shape[0])]
tsplot(x='index', y='bill', estimator=np.median, ax=axes[0,0], data=df_bill)
df_pay = DataFrame(data=df[num_var_pay].values.ravel(), columns=['pay'])
df_pay['index'] = [(i % 6 + 1) for i in range(df_bill.shape[0])]
tsplot(x='index', y='pay', estimator=np.median, ax=axes[0,1], data=df_pay)
df_bill = DataFrame(data=default[num_var_bill[1:]].values.ravel(), columns=['bill'])
df_bill['index'] = [(i % 6 + 1) for i in range(df_bill.shape[0])]
tsplot(x='index', y='bill', estimator=np.median, ax=axes[1,0], data=df_bill)
df_pay = DataFrame(data=default[num_var_pay].values.ravel(), columns=['pay'])
df_pay['index'] = [(i % 6 + 1) for i in range(df_bill.shape[0])]
tsplot(x='index', y='pay', estimator=np.median, ax=axes[1,1], data=df_pay)
df_bill = DataFrame(data=sample[num_var_bill[1:]].values.ravel(), columns=['bill'])
df_bill['index'] = [(i % 6 + 1) for i in range(df_bill.shape[0])]
tsplot(x='index', y='bill', estimator=np.median, ax=axes[2,0], data=df_bill)
df_pay = DataFrame(data=sample[num_var_pay].values.ravel(), columns=['pay'])
df_pay['index'] = [(i % 6 + 1) for i in range(df_bill.shape[0])]
tsplot(x='index', y='pay', estimator=np.median, ax=axes[2,1], data=df_pay);
<Figure size 1440x720 with 0 Axes>
df_resample = p.concat([df[df['Y']==1], df[df['Y']==0].sample(len(df[df['Y']==1]))])
for v in cat_var[:-1]:
print("Variable {}\n".format(v), p.crosstab(df_resample['Y'],df_resample[v]))
Variable SEX
SEX 1 2
Y
0 1932 3048
1 2160 2820
Variable EDUCATION
EDUCATION 0 1 2 3 4 5 6
Y
0 1 1816 2265 804 21 62 11
1 0 1498 2516 937 7 17 5
Variable MARRIAGE
MARRIAGE 0 1 2 3
Y
0 12 2218 2698 52
1 5 2443 2464 68
Variable PAY_0
PAY_0 -1 -2 0 1 2 3 4 5 6 7 8
Y
0 1008 510 2749 499 189 13 6 4 1 0 1
1 712 279 1447 901 1371 200 39 12 4 7 8
Variable PAY_2
PAY_2 -1 -2 0 1 2 3 4 5 6 7
Y
0 1111 661 2826 4 339 26 9 3 0 1
1 728 497 1903 5 1616 161 43 11 8 8
Variable PAY_3
PAY_3 -1 -2 0 1 2 3 4 5 6 7 8
Y
0 1096 721 2758 1 376 18 5 2 1 2 0
1 696 555 2087 1 1469 109 31 9 8 14 1
Variable PAY_4
PAY_4 -1 -2 0 1 2 3 4 5 6 7 8
Y
0 1028 778 2845 1 300 17 4 4 1 2 0
1 680 607 2280 1 1249 81 34 12 0 35 1
Variable PAY_5
PAY_5 -1 -2 0 2 3 4 5 6 7 8
Y
0 1018 798 2912 231 11 6 2 0 2 0
1 658 663 2407 1090 80 36 9 1 35 1
Variable PAY_6
PAY_6 -1 -2 0 2 3 4 5 6 7 8
Y
0 1045 865 2773 273 16 4 0 2 2 0
1 716 735 2308 1068 85 23 6 10 28 1
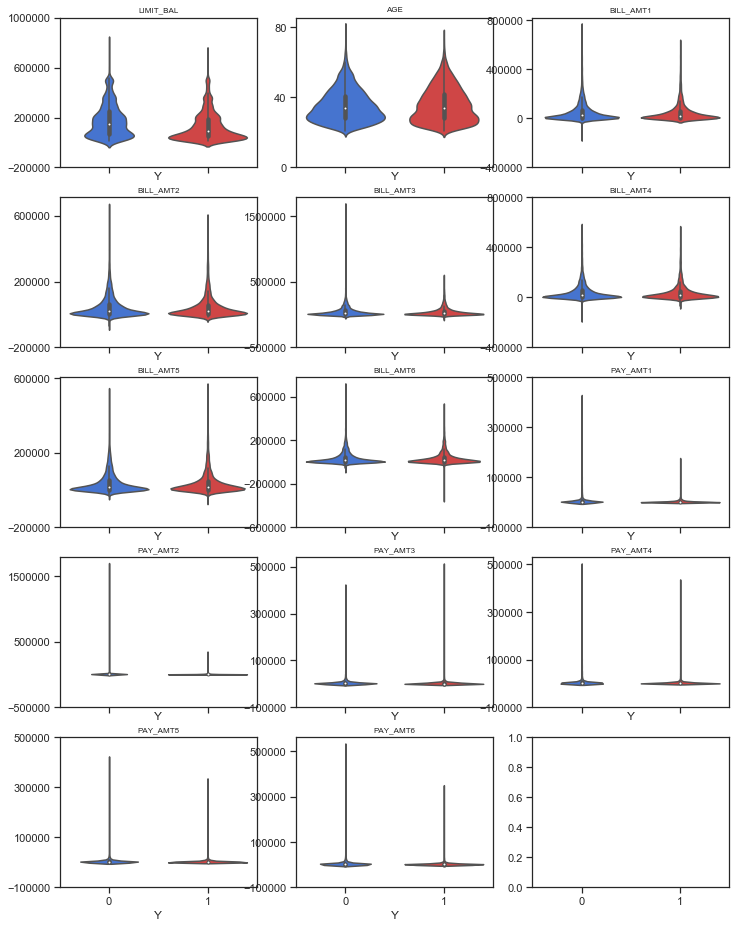
Variables numériques (sur un sample d’individus)#
%matplotlib inline
import matplotlib.pyplot as plt
fig, axes = plt.subplots(5,3, sharex=True, figsize=(12,16))
for i in range(5):
for j in range(3):
if i*3+j < len(num_var) :
axes[i,j].set_title(num_var[i*3+j],fontsize=8)
sns.violinplot(x="Y", y=num_var[i*3+j], \
data=df_resample, palette=["#2F6CE6","#E62F2F"], ax = axes[i,j])
#sns.stripplot(x="Y", y=num_var[i*3+j], \
# data=df_resample, palette=["#2F6CE6","#E62F2F"], jitter=True, ax = axes[i,j])
axes[i,j].set_ylabel('')
yticks=axes[i,j].get_yticks()
axes[i,j].set_yticks(yticks[::2])
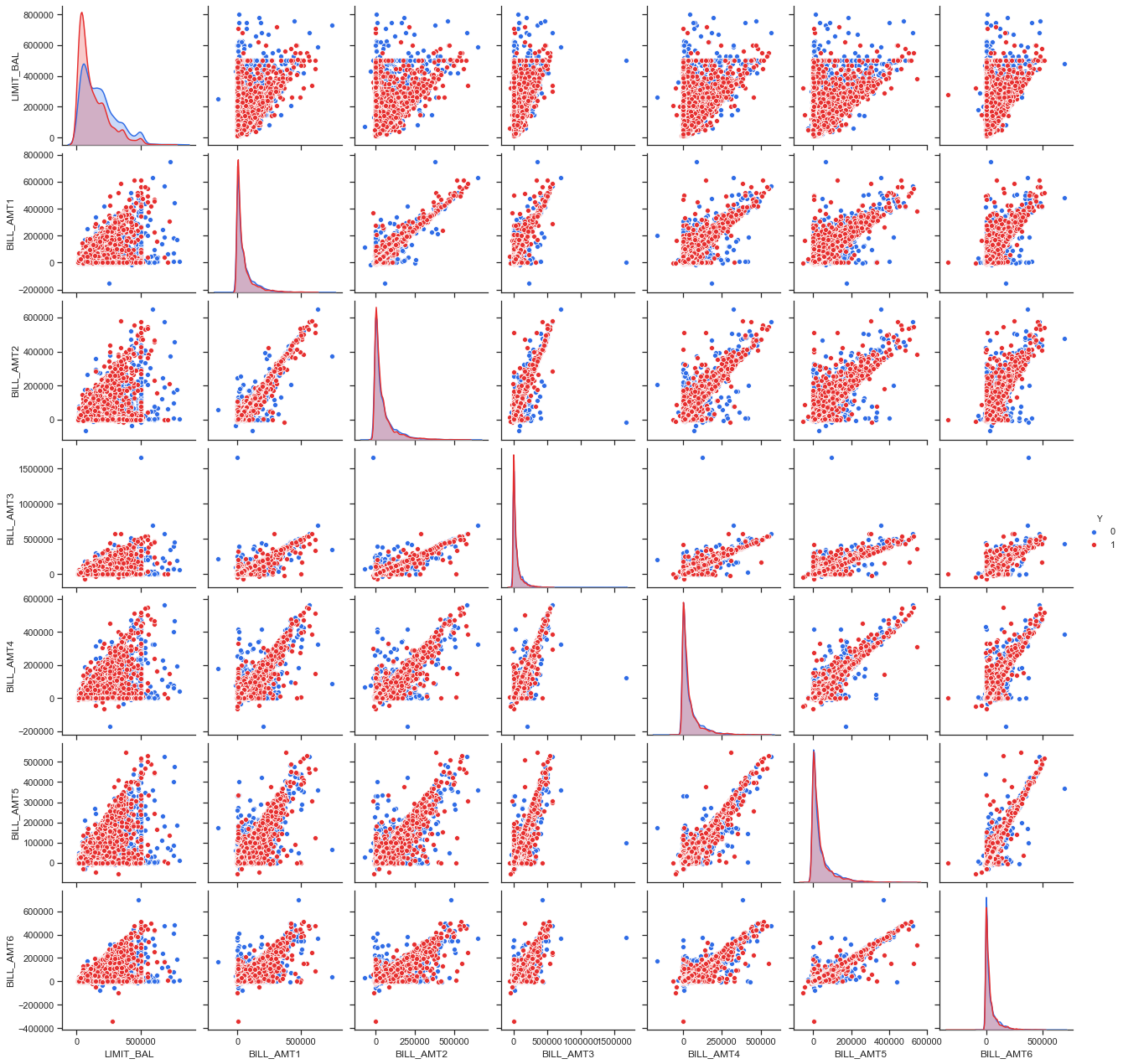
import seaborn as sns
sns.set(style="ticks")
sns.pairplot(df_resample[num_var_bill + ['Y']], hue='Y', palette=["#2F6CE6","#E62F2F"]);
import seaborn as sns
sns.set(style="ticks")
sns.pairplot(df_resample[num_var_pay + ['Y']], hue='Y', palette=["#2F6CE6","#E62F2F"]);
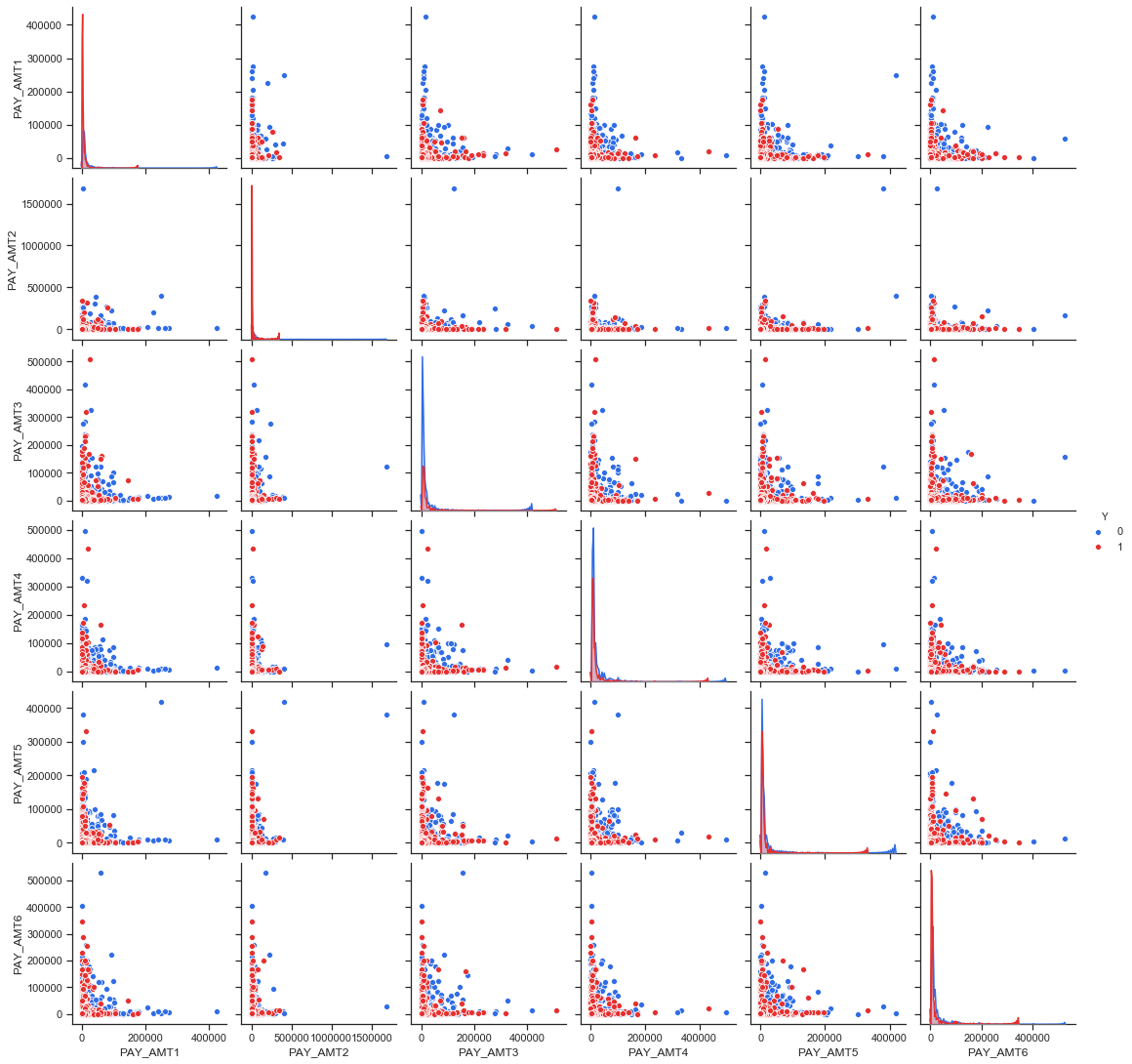
Idées pouvant être explorées : - le default doit pouvoir se repérer dans la décélération des remboursements. - il y a aussi peut etre un effet “biais du survivant” : les users qui sont repérés comme susceptibles d’entraîner un défaut => montant de crédits accordés plus petits. - multicolinéarité de nombreuses variables => faire une ACP au préalable