1A - Enoncé 24 novembre 2020#
Links: notebook, html, python, slides, GitHub
Correction de l’examen du 24 novembre 2020.
from jyquickhelper import add_notebook_menu
add_notebook_menu()
Exercice 1 : guérison#
On commence par générer des données artificielles à partir de véritables données.
import pandas
df = pandas.read_csv("https://www.data.gouv.fr/en/datasets/r/63352e38-d353-4b54-bfd1-f1b3ee1cabd7", sep=";")
gr = df[["jour", "rad", "dc"]].groupby(["jour"]).sum()
gr.head()
| rad | dc | |
|---|---|---|
| jour | ||
| 2020-03-18 | 1627 | 435 |
| 2020-03-19 | 2322 | 642 |
| 2020-03-20 | 3128 | 890 |
| 2020-03-21 | 3580 | 1041 |
| 2020-03-22 | 4188 | 1251 |
diff = gr.diff().reset_index(drop=False)
diff.head()
| jour | rad | dc | |
|---|---|---|---|
| 0 | 2020-03-18 | NaN | NaN |
| 1 | 2020-03-19 | 695.0 | 207.0 |
| 2 | 2020-03-20 | 806.0 | 248.0 |
| 3 | 2020-03-21 | 452.0 | 151.0 |
| 4 | 2020-03-22 | 608.0 | 210.0 |
On convertit la date en jour de l’année puis on simule un loi exponentielle de paramètre 14 pour avoir la date de sortie.
import numpy.random as rnd
def donnees_artificielles(hosp, mu=14, nu=21):
dt = pandas.to_datetime(hosp['jour'])
res = []
for i in range(hosp.shape[0]):
date = dt[i].dayofyear
h = hosp.iloc[i, 1]
delay = rnd.exponential(mu, int(h))
for j in range(delay.shape[0]):
res.append([date - int(delay[j]), date, 1])
h = hosp.iloc[i, 2]
delay = rnd.exponential(nu, int(h))
for j in range(delay.shape[0]):
res.append([date - int(delay[j]), date , 0])
return pandas.DataFrame(res, columns=["entree", "sortie", "issue"])
data = donnees_artificielles(diff[1:].reset_index(drop=True))
data.head()
| entree | sortie | issue | |
|---|---|---|---|
| 0 | 39 | 79 | 1 |
| 1 | 71 | 79 | 1 |
| 2 | 58 | 79 | 1 |
| 3 | 79 | 79 | 1 |
| 4 | 53 | 79 | 1 |
data.to_csv("examen2021.csv", index=False)
Q1#
On récupère les données.
import pandas
df = pandas.read_csv("http://www.xavierdupre.fr/enseignement/complements/examen2021.zip")
df.head()
| entree | sortie | issue | |
|---|---|---|---|
| 0 | 49 | 79 | 1 |
| 1 | 27 | 79 | 1 |
| 2 | 73 | 79 | 1 |
| 3 | 74 | 79 | 1 |
| 4 | 48 | 79 | 1 |
Q2 : durée de guérison#
duree = df['sortie'] - df['entree']
duree = duree.values # conversion en numpy
issue = df['issue'].values
duree[:5], issue[:5]
(array([30, 52, 6, 5, 31], dtype=int64), array([1, 1, 1, 1, 1], dtype=int64))
Q3 : estimateur Kaplan-Meier (1)#
t = 10
nt = duree[(duree >= t)].shape[0]
dt = duree[(duree == t) & (issue == 0)].shape[0]
st = 1. - dt / nt
st
0.98965342710248
Q4 : courbe de Kaplan-Meier#
T = [0]
St = [1.]
for t in range(0, 150):
nt = duree[(duree >= t)].shape[0]
dt = duree[(duree == t) & (issue == 0)].shape[0]
st = 1. - dt / nt
T.append(t)
St.append(st * St[-1])
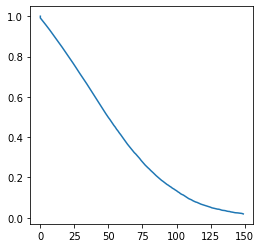
Q5 : graphe#
import matplotlib.pyplot as plt
fig, ax = plt.subplots(1, 1, figsize=(4, 4))
ax.plot(T, St);
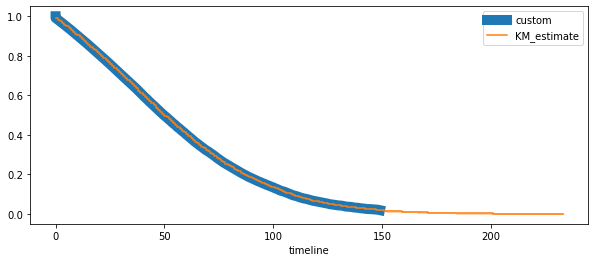
import numpy
from lifelines import KaplanMeierFitter
fig, ax = plt.subplots(1, 1, figsize=(10, 4))
ax.plot(T, St, label="custom", lw=10)
kmf = KaplanMeierFitter()
kmf.fit(duree, (issue == 0).astype(numpy.int32))
kmf.plot(ax=ax)
ax.legend();
Q6 : application aux données publiques#
Les données accessibles librement sur le portail data.gouv.fr recensent les entrées et les sorties des personnes sans relier une entrée et une sortie spécifique. Si N est personnes sont sorties guéries, on ne sait pas quand elles sont entrées. Donc le calcul ci-dessus n’est pas possible.
Exercice 2#
Q1 : t + 1#
import numpy
N = 10
M = numpy.zeros((N, N))
M[4, 5] = 1
M
array([[0., 0., 0., 0., 0., 0., 0., 0., 0., 0.],
[0., 0., 0., 0., 0., 0., 0., 0., 0., 0.],
[0., 0., 0., 0., 0., 0., 0., 0., 0., 0.],
[0., 0., 0., 0., 0., 0., 0., 0., 0., 0.],
[0., 0., 0., 0., 0., 1., 0., 0., 0., 0.],
[0., 0., 0., 0., 0., 0., 0., 0., 0., 0.],
[0., 0., 0., 0., 0., 0., 0., 0., 0., 0.],
[0., 0., 0., 0., 0., 0., 0., 0., 0., 0.],
[0., 0., 0., 0., 0., 0., 0., 0., 0., 0.],
[0., 0., 0., 0., 0., 0., 0., 0., 0., 0.]])
def propagation(M):
M2 = M.copy()
M2[1:, :] = numpy.maximum(M2[1:, :], M[:-1, :])
M2[:-1, :] = numpy.maximum(M2[:-1, :], M[1:, :])
M2[:, 1:] = numpy.maximum(M2[:, 1:], M[:, :-1])
M2[:, :-1] = numpy.maximum(M2[:, :-1], M[:, 1:])
return M2
propagation(M.copy())
array([[0., 0., 0., 0., 0., 0., 0., 0., 0., 0.],
[0., 0., 0., 0., 0., 0., 0., 0., 0., 0.],
[0., 0., 0., 0., 0., 0., 0., 0., 0., 0.],
[0., 0., 0., 0., 0., 1., 0., 0., 0., 0.],
[0., 0., 0., 0., 1., 1., 1., 0., 0., 0.],
[0., 0., 0., 0., 0., 1., 0., 0., 0., 0.],
[0., 0., 0., 0., 0., 0., 0., 0., 0., 0.],
[0., 0., 0., 0., 0., 0., 0., 0., 0., 0.],
[0., 0., 0., 0., 0., 0., 0., 0., 0., 0.],
[0., 0., 0., 0., 0., 0., 0., 0., 0., 0.]])
Q2 : après T itération#
def propagation_n(M, t):
for i in range(t):
M = propagation(M)
return M
propagation_n(M, 3)
array([[0., 0., 0., 0., 0., 0., 0., 0., 0., 0.],
[0., 0., 0., 0., 0., 1., 0., 0., 0., 0.],
[0., 0., 0., 0., 1., 1., 1., 0., 0., 0.],
[0., 0., 0., 1., 1., 1., 1., 1., 0., 0.],
[0., 0., 1., 1., 1., 1., 1., 1., 1., 0.],
[0., 0., 0., 1., 1., 1., 1., 1., 0., 0.],
[0., 0., 0., 0., 1., 1., 1., 0., 0., 0.],
[0., 0., 0., 0., 0., 1., 0., 0., 0., 0.],
[0., 0., 0., 0., 0., 0., 0., 0., 0., 0.],
[0., 0., 0., 0., 0., 0., 0., 0., 0., 0.]])
Q3 : vaccin#
p = 0.3
vaccine = (numpy.random.rand(N, N) <= p).astype(numpy.int32)
vaccine
array([[0, 0, 0, 0, 0, 0, 1, 0, 1, 0],
[0, 0, 0, 0, 0, 0, 1, 0, 0, 1],
[1, 0, 0, 0, 0, 0, 1, 0, 1, 1],
[0, 1, 0, 1, 0, 0, 0, 0, 0, 0],
[1, 0, 0, 0, 0, 0, 0, 0, 0, 0],
[0, 0, 1, 1, 0, 0, 1, 0, 1, 0],
[0, 0, 1, 0, 0, 0, 0, 1, 0, 0],
[0, 0, 1, 0, 0, 0, 1, 0, 0, 1],
[0, 0, 1, 0, 0, 0, 0, 1, 0, 0],
[0, 0, 0, 1, 0, 0, 0, 1, 0, 0]])
def propagation_vaccine(M, vaccine):
M2 = M.copy()
M2[1:, :] = numpy.maximum(M2[1:, :], M[:-1, :])
M2[:-1, :] = numpy.maximum(M2[:-1, :], M[1:, :])
M2[:, 1:] = numpy.maximum(M2[:, 1:], M[:, :-1])
M2[:, :-1] = numpy.maximum(M2[:, :-1], M[:, 1:])
M2 = numpy.minimum(M2, 1 - vaccine)
return M2
vaccine[4, 5] = 0
propagation_vaccine(M, vaccine)
array([[0., 0., 0., 0., 0., 0., 0., 0., 0., 0.],
[0., 0., 0., 0., 0., 0., 0., 0., 0., 0.],
[0., 0., 0., 0., 0., 0., 0., 0., 0., 0.],
[0., 0., 0., 0., 0., 1., 0., 0., 0., 0.],
[0., 0., 0., 0., 1., 1., 1., 0., 0., 0.],
[0., 0., 0., 0., 0., 1., 0., 0., 0., 0.],
[0., 0., 0., 0., 0., 0., 0., 0., 0., 0.],
[0., 0., 0., 0., 0., 0., 0., 0., 0., 0.],
[0., 0., 0., 0., 0., 0., 0., 0., 0., 0.],
[0., 0., 0., 0., 0., 0., 0., 0., 0., 0.]])
Q4 : après T heures#
def propagation_n_vaccine(M, t, vaccine):
for i in range(t):
M = propagation_vaccine(M, vaccine)
return M
propagation_n_vaccine(M, 3, vaccine)
array([[0., 0., 0., 0., 0., 0., 0., 0., 0., 0.],
[0., 0., 0., 0., 0., 1., 0., 0., 0., 0.],
[0., 0., 0., 0., 1., 1., 0., 0., 0., 0.],
[0., 0., 0., 0., 1., 1., 1., 1., 0., 0.],
[0., 0., 1., 1., 1., 1., 1., 1., 1., 0.],
[0., 0., 0., 0., 1., 1., 0., 1., 0., 0.],
[0., 0., 0., 0., 1., 1., 1., 0., 0., 0.],
[0., 0., 0., 0., 0., 1., 0., 0., 0., 0.],
[0., 0., 0., 0., 0., 0., 0., 0., 0., 0.],
[0., 0., 0., 0., 0., 0., 0., 0., 0., 0.]])
Q5 : variation#
import pandas
res = []
for p in [0.7, 0.8, 0.85, 0.86, 0.87, 0.88, 0.89, 0.9, 0.94, 0.95, 0.96, 0.97, 0.98, 0.99, 1.0]:
cont = []
for test in range(0, 10):
vaccine = (numpy.random.rand(N, N) <= p).astype(numpy.int32)
M[4, 5] = 1
vaccine[4, 5] = 0
M = propagation_n_vaccine(M, 3, vaccine)
contamine = M.ravel().sum()
cont.append(contamine)
cont = numpy.array(cont)
res.append(dict(p=p, prop=cont.mean()))
df = pandas.DataFrame(res)
df
| p | prop | |
|---|---|---|
| 0 | 0.70 | 9.1 |
| 1 | 0.80 | 9.6 |
| 2 | 0.85 | 3.8 |
| 3 | 0.86 | 2.4 |
| 4 | 0.87 | 2.4 |
| 5 | 0.88 | 1.4 |
| 6 | 0.89 | 1.6 |
| 7 | 0.90 | 1.2 |
| 8 | 0.94 | 1.2 |
| 9 | 0.95 | 1.5 |
| 10 | 0.96 | 1.0 |
| 11 | 0.97 | 1.2 |
| 12 | 0.98 | 1.2 |
| 13 | 0.99 | 1.1 |
| 14 | 1.00 | 1.0 |
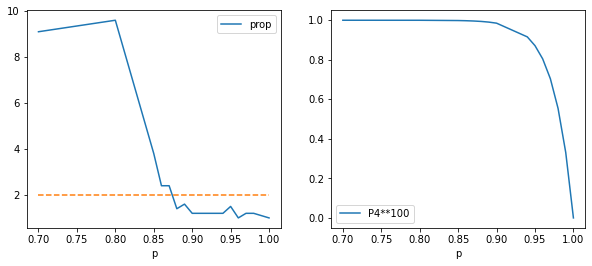
ax = df.plot(x="p", y="prop")
ax.plot([0.7, 1.], [2, 2], "--");
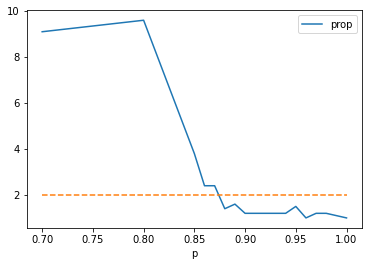
Dans cette configuration, en supposant qu’un seul élève est contaminé, il faudrait vacciner à plus de 85% pour avoir une chance de ne pas avoir une nouvelle contamination.
Ce résultat ne change pas si la taille de la matrice change. Il change
en revanche en fonction du nombre de tirages, ici 10. Pour n’avoir
aucune propagation, il faut entourer la personne contaminé de 4
personnes vaccinées. est la probabilité pour une personné
d’être vaccinée (ou immunisée si la vaccination est faite sur 100% des
personnes).
est la probabilité d’avoir 4 personnes
vaccinées.
est la probabilité qu’une personne ne soient
pas immunisées parmi les 4.
est la probabilité
que 10 cours de 3h se passent bien sans contamination.
p = 0.9
p4 = 1 - (1 - p) **4
p4
0.9999
df2 = df.copy()
df2["P4**100"] = 1 - df2["p"] ** 40
import matplotlib.pyplot as plt
fig, ax = plt.subplots(1, 2, figsize=(10, 4))
df2.plot(x="p", y="prop", ax=ax[0])
ax[0].plot([0.7, 1.], [2, 2], "--")
df2.plot(x="p", y="P4**100", ax=ax[1]);