Single Spectrum Analysis (SSA)#

Links: notebook, html, python, slides, GitHub

Illustration de la méthode SSA pour les séries temporelles appliquée à la détection de points aberrants. La méthode est décrite dans Singular Spectrum Analysis: Methodology and Comparison. Voir aussi Automated outlier detection in Singular Spectrum Analysis.

from jyquickhelper import add_notebook_menu
add_notebook_menu()

%matplotlib inline

Une série articielle#

On introduit quelques points aberrants, pour le reste, elle suit le modèle y_t = \frac{9}{10} y_{t-2} + \epsilon_t + a_t où a_t est le bruit aberrant qui survient quelques fois.

import numpy.random as rnd
import numpy
N = 2000
bruit1 = rnd.normal(size=(N,))
temps = numpy.arange(N)
bruit1[:5], temps[:5]

(array([-0.42127366, -0.80614375,  1.87947411,  0.13890672,  0.55054172]),
 array([0, 1, 2, 3, 4]))

On crée un bruit aberrant.

import random
bruit2 = numpy.zeros((N,))
for i in range(0, 10):
    h = random.randint(0, N-1)
    bruit2[h] = rnd.normal() + 10

serie = []
y = 10
for i in range(N//2+100):
    serie.append(y + bruit1[i] + 0.0004 * temps[i] + bruit2[i])
    if i > 30:
        y = 0.9 * serie[-2]
Y = numpy.array(serie[-1000:])
Y[:5]

array([ 0.35328897,  0.43350731, -0.25385586,  1.62514162,  0.09987641])

import matplotlib.pyplot as plt
fig, ax = plt.subplots(1, 2, figsize=(12, 4))
ax[0].plot(numpy.arange(len(Y)), Y)
ax[1].plot(numpy.arange(800, 900), Y[800:900])
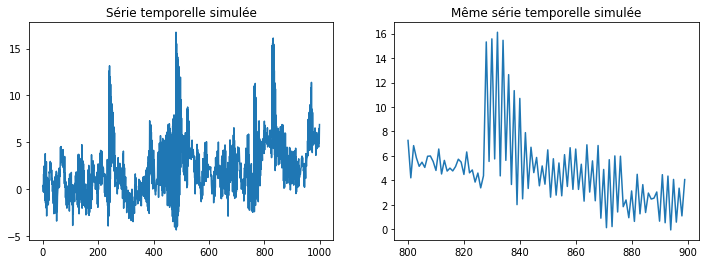
ax[0].set_title("Série temporelle simulée")
ax[1].set_title("Même série temporelle simulée");
../_images/timeseries_ssa_8_0.png

Autocorrélations#

L’autocorrélogramme est définie par la série cor(Y_t, Y_{t-d})_d. On le calcule sur la série nettoyée de sa tendance.

from pandas import DataFrame
df = DataFrame(dict(Y=Y))
df.head()
Y
0 0.353289
1 0.433507
2 -0.253856
3 1.625142
4 0.099876 
from statsmodels.tsa.tsatools import detrend
df["notrend"] = detrend(df.Y)
df.head()
Y notrend
0 0.353289 0.216265
1 0.433507 0.292403
2 -0.253856 -0.399040
3 1.625142 1.475877
4 0.099876 -0.053468 
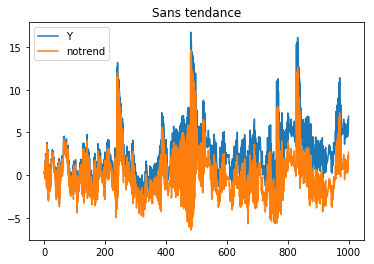
ax = df.plot()
ax.set_title("Sans tendance");
../_images/timeseries_ssa_12_0.png

L’autocorrélogramme à proprement parler.

from statsmodels.tsa.stattools import acf
cor = acf(df.notrend)
fig, ax = plt.subplots(1, 1)
ax.plot(cor)
ax.set_title("Autocorrélogramme");
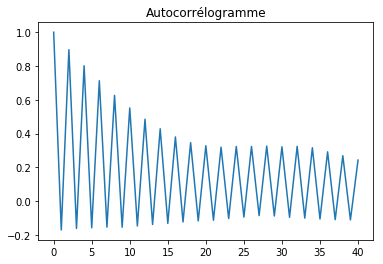
../_images/timeseries_ssa_14_0.png

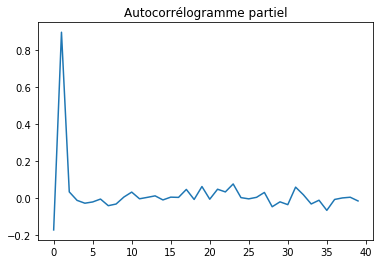
Etant donnée que la série Y_t dépend de Y_{t-2}, on observe un pic pour cor(Y_t, Y_{t-2})_d et pour tous les d pairs. cor(Y_t, Y_{t-4}) \sim cor(Y_t, Y_{t-2})^2. On enlève ces effets récursifs en calculant l’autocorrélogramme partiel qui correspond à l’estimation des coefficients d’un modèle autorégressif infini.

from statsmodels.tsa.stattools import pacf
pcor = pacf(df.notrend)
fig, ax = plt.subplots(1, 1)
ax.plot(pcor[1:])
ax.set_title("Autocorrélogramme partiel");
../_images/timeseries_ssa_16_0.png

SSA#

Ou Singular Spectrum Analysis. La méthode part de la matrice des séries décalées qu’on décompose avec la méthode SVD ou Singular Value Decomposition.

def lagged_ts(serie, lag):
    dim = serie.shape[0]
    res = numpy.zeros((dim - lag + 1, lag))
    for i in range(lag):
        res[:, i] = serie[i:dim-lag+i+1]
    return res

lagged_ts(Y, 3)

array([[ 0.35328897,  0.43350731, -0.25385586],
       [ 0.43350731, -0.25385586,  1.62514162],
       [-0.25385586,  1.62514162,  0.09987641],
       ...,
       [ 5.59900199,  4.51154279,  6.48711916],
       [ 4.51154279,  6.48711916,  4.94491822],
       [ 6.48711916,  4.94491822,  6.90403987]])

lag = lagged_ts(Y, 60)
lag.shape

(941, 60)

from numpy.linalg import svd
# u @ numpy.diag(s) @ vh
u, s, vh = svd(lag)

u.shape, s.shape, vh.shape

((941, 941), (60,), (60, 60))

d = numpy.zeros((941, 60))
d[:60,:60] = numpy.diag(s)

(u @ d @ vh).shape

(941, 60)

fig, ax = plt.subplots(1,2, figsize=(12,4))
DataFrame(dict(valeur=s)).plot(kind="bar", ax=ax[0])
DataFrame(dict(valeur=s[1:15])).plot(kind="bar", ax=ax[1])
ax[0].set_title("Valeurs propres")
ax[1].set_title("Valeurs propres sans la première");
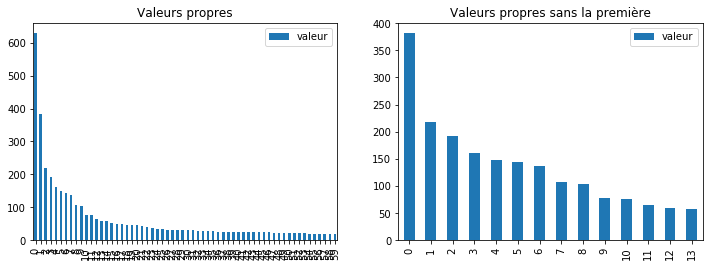
../_images/timeseries_ssa_24_0.png

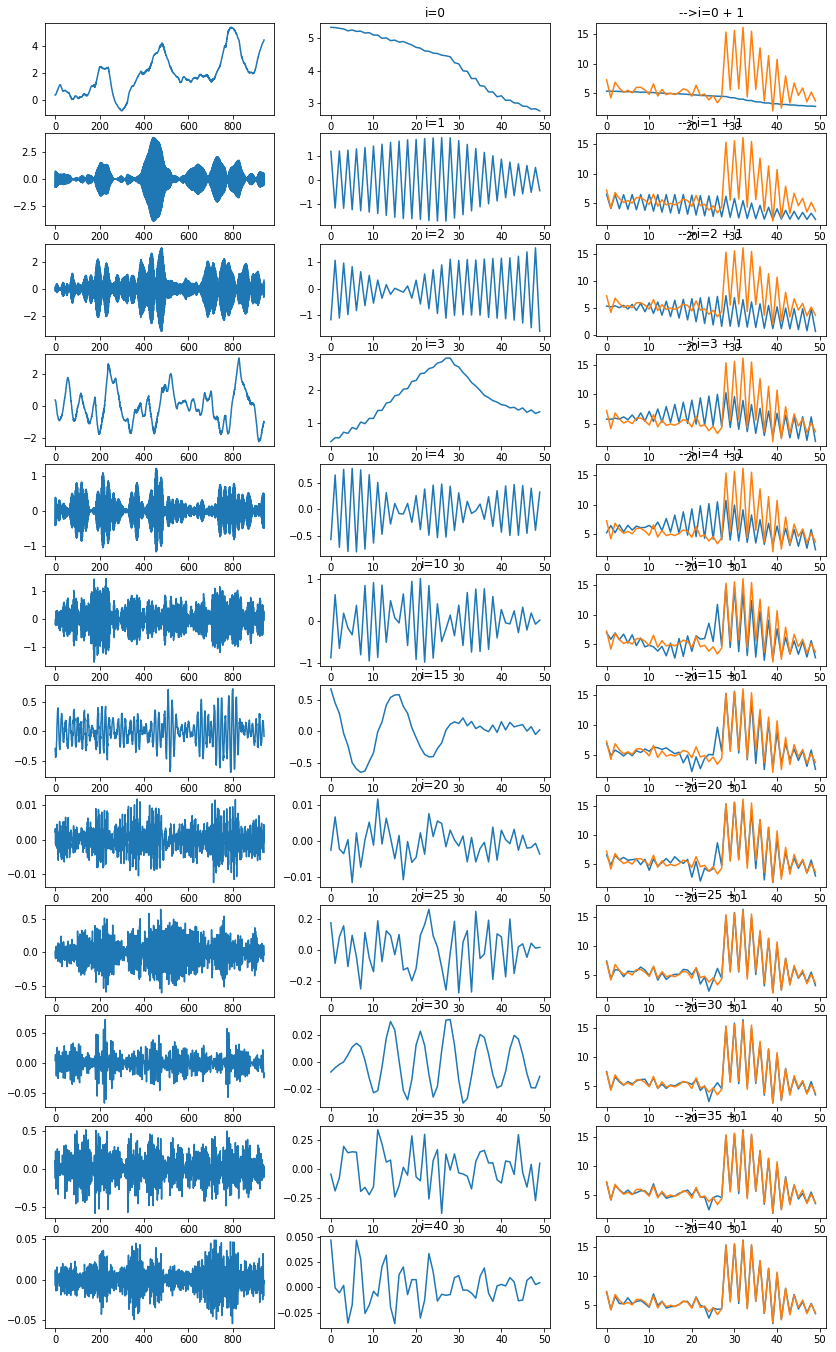
Je me représente la méthode SVD comme une façon de projeter des vecteurs sur l’espace vectoriel constitué des premiers vecteurs propres, à chaque dimension supplémentaire, c’est comme une pièce du puzzle qui s’assemble jusqu’à recomposer l’ensemble. Ce qu’on peut voir aussi comme ceci :

np = 12
fig, ax = plt.subplots(np, 3, figsize=(14, np*2))
for n in range(np):
    i = n if n < 5 else n * 5 - 15
    d = numpy.zeros((941, 60))
    d[i, i] = s[i]
    X2 = u @ d @ vh
    pos = 0 #X2.shape[1] - 1

    # série reconstruites avec un axe
    ax[n, 0].plot(X2[:,pos])
    ax[n, 1].set_title("i=%d" % i)
    # série reconstruites avec un axe
    ax[n, 1].plot(X2[800:850,pos])
    ax[n, 1].set_title("i=%d" % i)

    d = numpy.zeros((941, 60))
    d[:i+1, :i+1] = numpy.diag(s[:i+1])
    X2 = u @ d @ vh
    ax[n, 2].plot(X2[800:850,pos])
    ax[n, 2].plot(Y[800:850])
    ax[n, 2].set_title("-->i=%d + 1" % i)
../_images/timeseries_ssa_26_0.png

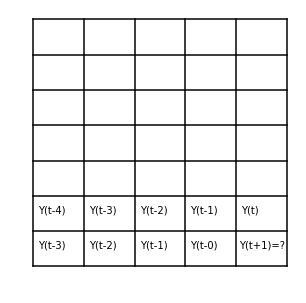
La prédiction#

On veut prédire Y_{t+1}. L’idée consiste à appliquer la méthode en considérent Y_{t+1} égale à Y_t puis à remplacer cette prédiction par la valeur de la série reconstruite. On peut même prédire à un horizon plus grand que la valeur suivante.

fig, ax = plt.subplots(1, 1, figsize=(5,5))
for i in range(0, 8):
    ax.plot([0, 5], [i, i], 'k-')
    if i < 6:
        ax.plot([i, i], [0, 7], 'k-')
    if i < 4:
        ax.text(i + 0.1, 1.5, "Y(t-%d)" % (4-i))
        ax.text(i + 0.1, 0.5, "Y(t-%d)" % (3-i))
ax.text(4.1, 1.5, "Y(t)")
ax.text(4.05, 0.5, "Y(t+1)=?")
plt.axis('off');
../_images/timeseries_ssa_28_0.png

Les points aberrants#

On repère les points aberrants avec l’une méthode de son choix sur la série reconstruite.

d = numpy.zeros((941, 60))
for i in range(0, 30):
    d[i, i] = s[i]
X2 = u @ d @ vh

from sklearn.covariance import EllipticEnvelope
env = EllipticEnvelope(support_fraction=0.9)
env.fit(X2[:,:30])

EllipticEnvelope(assume_centered=False, contamination=0.1, random_state=None,
         store_precision=True, support_fraction=0.9)

L’idéal serait d’utiliser une méthode basée sur une ACP. Le plus proche reste le modèle gaussien avec EllipticEnvelope.

out = env.predict(X2[:,:30])

fig, ax = plt.subplots(1, 1, figsize=(12,2))
ax.plot((1 - out)/2, "-")
ax.set_title("Points aberrants d'une série temporelles.");
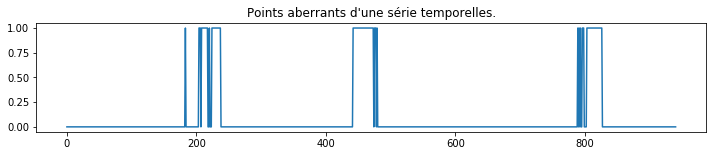
../_images/timeseries_ssa_33_0.png

On observe des plages contiguës. Cela signifie que d’une valeur aberrante contamine des vecteurs décalées consécutifs de la série Y. Il ne reste plus qu’à repérer la valeur incriminée.

fig, ax = plt.subplots(1, 1, figsize=(14,2))
ax.plot(X2[:,0], label="serie")
ax.plot((1 - out)*5, "-", label="outlier")
ax.set_title("Points aberrants sur la série reconstruite")
ax.legend();
../_images/timeseries_ssa_35_0.png 
fig, ax = plt.subplots(1, 1, figsize=(14,2))
ax.plot(Y, label="serie")
ax.plot((1 - out)*5, "-", label="outlier")
ax.set_title("Points aberrants sur la série brute")
ax.legend();
../_images/timeseries_ssa_36_0.png

Ce qui a l’air de correspondre à la fin des grandes plages. On recommence avec la probabilité d’être un outlier.

fig, ax = plt.subplots(1, 1, figsize=(14,2))
outp = env.decision_function(X2[:,:30])
ax.plot(Y, label="serie")
ax.plot(outp, "-", label="Proba not outlier")
ax.set_title("Points aberrants sur la série brute")
ax.legend();
../_images/timeseries_ssa_38_0.png