1A.1 - Intégrale et la méthode des rectangles#

Links: notebook, html, python, slides, GitHub

Approximation du calcul d’une intégrale par la méthode des rectangles

from jyquickhelper import add_notebook_menu
add_notebook_menu()

Calcul de l’intégrale#

On cherche à calculer une intégrale en utilisant la méthode des rectangles.

from pyquickhelper.helpgen import NbImage
NbImage("images/int.png")
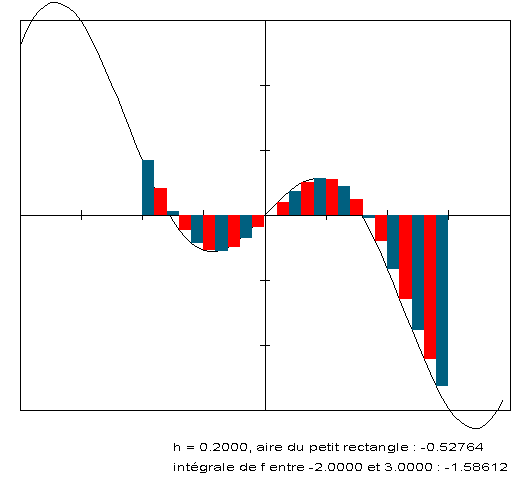
../_images/integrale_rectangle_3_0.png

L’intervalle de l’intégrale est noté [a,b] et la fonction à intégrer f. On divise cet intervalle en n petits segments et on fait la somme des aires des petits rectangles délimités par l’axe des abscisses et la courbe de la fonction f.

\int_a^b f(x) dx \approx \frac{b-a}{n} \; \sum_{i=1}^{n} f\left( a + i \frac{b-a}{n}\right)

On pourra prendre par exemple :

a = -2
b = 3
n = 20

Et comme fonction :

import math
f = lambda x: x * math.cos (x)
f(4)

-2.6145744834544478

Il faut écrire la fonction qui calcule l’intégrale.

Calcul de précision#

Quelle valeur de n faut-il choisir pour être précis à 10^{-4} près ? Ecrire la fonction qui permette de calculer cette valeur.

Calcul plus rapide#

La réponde naïve à la question précédente est assez peu performante. Voyez-vous un moyen d’aller plus vite ?