Hyperparamètres, LassoRandomForestRregressor et grid_search (correction)#
Links: notebook, html, python, slides, GitHub
Le notebook explore l’optimisation des hyper paramaètres du modèle LassoRandomForestRegressor, et fait varier le nombre d’arbre et le paramètres alpha.
from jyquickhelper import add_notebook_menu
add_notebook_menu()
%matplotlib inline
Données#
from sklearn.datasets import load_diabetes
from sklearn.model_selection import train_test_split
data = load_diabetes()
X, y = data.data, data.target
X_train, X_test, y_train, y_test = train_test_split(X, y)
Premiers modèles#
from sklearn.ensemble import RandomForestRegressor
from sklearn.metrics import r2_score
rf = RandomForestRegressor()
rf.fit(X_train, y_train)
r2_score(y_test, rf.predict(X_test))
0.3166064611454491
Pour le modèle, il suffit de copier coller le code écrit dans ce fichier lasso_random_forest_regressor.py.
from ensae_teaching_cs.ml.lasso_random_forest_regressor import LassoRandomForestRegressor
lrf = LassoRandomForestRegressor()
lrf.fit(X_train, y_train)
r2_score(y_test, lrf.predict(X_test))
0.20558896981102492
Le modèle a réduit le nombre d’arbres.
len(lrf.estimators_)
97
Grid Search#
On veut trouver la meilleure paire de paramètres (n_estimators,
alpha). scikit-learn implémente l’objet
GridSearchCV
qui effectue de nombreux apprentissage avec toutes les valeurs de
paramètres qu’il reçoit. Voici tous les paramètres qu’on peut changer :
lrf.get_params()
{'lasso_estimator__alpha': 1.0,
'lasso_estimator__copy_X': True,
'lasso_estimator__fit_intercept': True,
'lasso_estimator__max_iter': 1000,
'lasso_estimator__positive': False,
'lasso_estimator__precompute': False,
'lasso_estimator__random_state': None,
'lasso_estimator__selection': 'cyclic',
'lasso_estimator__tol': 0.0001,
'lasso_estimator__warm_start': False,
'lasso_estimator': Lasso(),
'rf_estimator__bootstrap': True,
'rf_estimator__ccp_alpha': 0.0,
'rf_estimator__criterion': 'squared_error',
'rf_estimator__max_depth': None,
'rf_estimator__max_features': 1.0,
'rf_estimator__max_leaf_nodes': None,
'rf_estimator__max_samples': None,
'rf_estimator__min_impurity_decrease': 0.0,
'rf_estimator__min_samples_leaf': 1,
'rf_estimator__min_samples_split': 2,
'rf_estimator__min_weight_fraction_leaf': 0.0,
'rf_estimator__n_estimators': 100,
'rf_estimator__n_jobs': None,
'rf_estimator__oob_score': False,
'rf_estimator__random_state': None,
'rf_estimator__verbose': 0,
'rf_estimator__warm_start': False,
'rf_estimator': RandomForestRegressor()}
params = {
'lasso_estimator__alpha': [0.25, 0.5, 0.75, 1., 1.25, 1.5],
'rf_estimator__n_estimators': [20, 40, 60, 80, 100, 120]
}
from sklearn.exceptions import ConvergenceWarning
from sklearn.model_selection import GridSearchCV
import warnings
warnings.filterwarnings("ignore", category=ConvergenceWarning)
grid = GridSearchCV(estimator=LassoRandomForestRegressor(),
param_grid=params, verbose=1)
grid.fit(X_train, y_train)
Fitting 5 folds for each of 36 candidates, totalling 180 fits
GridSearchCV(estimator=LassoRandomForestRegressor(lasso_estimator=Lasso(),
rf_estimator=RandomForestRegressor()),
param_grid={'lasso_estimator__alpha': [0.25, 0.5, 0.75, 1.0, 1.25,
1.5],
'rf_estimator__n_estimators': [20, 40, 60, 80, 100,
120]},
verbose=1)In a Jupyter environment, please rerun this cell to show the HTML representation or trust the notebook. On GitHub, the HTML representation is unable to render, please try loading this page with nbviewer.org.
GridSearchCV(estimator=LassoRandomForestRegressor(lasso_estimator=Lasso(),
rf_estimator=RandomForestRegressor()),
param_grid={'lasso_estimator__alpha': [0.25, 0.5, 0.75, 1.0, 1.25,
1.5],
'rf_estimator__n_estimators': [20, 40, 60, 80, 100,
120]},
verbose=1)LassoRandomForestRegressor(lasso_estimator=Lasso(),
rf_estimator=RandomForestRegressor())Lasso()
Lasso()
RandomForestRegressor()
RandomForestRegressor()
Les meilleurs paramètres sont les suivants :
grid.best_params_
{'lasso_estimator__alpha': 0.25, 'rf_estimator__n_estimators': 20}
Et le modèle a gardé un nombre réduit d’arbres :
len(grid.best_estimator_.estimators_)
20
r2_score(y_test, grid.predict(X_test))
0.23768343413832094
Evolution de la performance en fonction des paramètres#
grid.cv_results_
{'mean_fit_time': array([0.051863 , 0.11151867, 0.16286798, 0.20638132, 0.24587946,
0.30230732, 0.04886923, 0.10883999, 0.1585783 , 0.21171408,
0.25670881, 0.30813308, 0.04687281, 0.10599108, 0.16779151,
0.21490512, 0.24286323, 0.37416844, 0.04798951, 0.10375576,
0.13916297, 0.19486108, 0.23168812, 0.35405369, 0.04832931,
0.10837116, 0.17046494, 0.21563282, 0.250454 , 0.30722728,
0.0500711 , 0.10197167, 0.14489303, 0.19933763, 0.31132407,
0.69930143]),
'std_fit_time': array([0.00362419, 0.01626225, 0.00804797, 0.01572331, 0.00662523,
0.01574959, 0.00169066, 0.0097691 , 0.0132841 , 0.0106317 ,
0.01988724, 0.02359756, 0.00126011, 0.00448715, 0.00627981,
0.02519122, 0.02605425, 0.09337497, 0.01102544, 0.00824485,
0.00715579, 0.01587819, 0.006515 , 0.04939259, 0.00602516,
0.00652839, 0.01898743, 0.01727985, 0.01794094, 0.02079929,
0.00562965, 0.00345422, 0.00807745, 0.00482911, 0.09500837,
0.11143193]),
'mean_score_time': array([0.00239778, 0.00359111, 0.00518904, 0.00718164, 0.00817652,
0.01257362, 0.0021884 , 0.00339103, 0.00539336, 0.00738797,
0.00917087, 0.00998683, 0.00199485, 0.00379586, 0.00599022,
0.0103807 , 0.01236439, 0.00837784, 0.00431471, 0.00392194,
0.00887637, 0.00752082, 0.00937295, 0.01437345, 0.00079789,
0.00312424, 0.00479422, 0.00718193, 0.00958648, 0.01098609,
0.00199614, 0.0039938 , 0.0049974 , 0.00697622, 0.01322117,
0.02559528]),
'std_score_time': array([8.11351379e-04, 4.87586231e-04, 3.98946617e-04, 3.98891227e-04,
4.01356881e-04, 4.68445598e-03, 3.86144056e-04, 4.75930831e-04,
4.96522489e-04, 1.36387385e-03, 1.15770100e-03, 1.41214662e-05,
1.39020727e-06, 4.03363736e-04, 6.28333254e-04, 9.76193348e-03,
6.18748536e-03, 4.21257447e-03, 5.70546749e-03, 6.04969222e-03,
6.08895072e-03, 4.95836569e-03, 7.65298131e-03, 2.73983497e-03,
9.77213669e-04, 6.24847412e-03, 2.48103089e-03, 3.95754917e-04,
2.06222335e-03, 1.41556299e-03, 1.58579723e-06, 1.09920549e-03,
1.70908708e-05, 6.18028043e-04, 2.94616536e-03, 1.07247410e-02]),
'param_lasso_estimator__alpha': masked_array(data=[0.25, 0.25, 0.25, 0.25, 0.25, 0.25, 0.5, 0.5, 0.5, 0.5,
0.5, 0.5, 0.75, 0.75, 0.75, 0.75, 0.75, 0.75, 1.0, 1.0,
1.0, 1.0, 1.0, 1.0, 1.25, 1.25, 1.25, 1.25, 1.25, 1.25,
1.5, 1.5, 1.5, 1.5, 1.5, 1.5],
mask=[False, False, False, False, False, False, False, False,
False, False, False, False, False, False, False, False,
False, False, False, False, False, False, False, False,
False, False, False, False, False, False, False, False,
False, False, False, False],
fill_value='?',
dtype=object),
'param_rf_estimator__n_estimators': masked_array(data=[20, 40, 60, 80, 100, 120, 20, 40, 60, 80, 100, 120, 20,
40, 60, 80, 100, 120, 20, 40, 60, 80, 100, 120, 20, 40,
60, 80, 100, 120, 20, 40, 60, 80, 100, 120],
mask=[False, False, False, False, False, False, False, False,
False, False, False, False, False, False, False, False,
False, False, False, False, False, False, False, False,
False, False, False, False, False, False, False, False,
False, False, False, False],
fill_value='?',
dtype=object),
'params': [{'lasso_estimator__alpha': 0.25, 'rf_estimator__n_estimators': 20},
{'lasso_estimator__alpha': 0.25, 'rf_estimator__n_estimators': 40},
{'lasso_estimator__alpha': 0.25, 'rf_estimator__n_estimators': 60},
{'lasso_estimator__alpha': 0.25, 'rf_estimator__n_estimators': 80},
{'lasso_estimator__alpha': 0.25, 'rf_estimator__n_estimators': 100},
{'lasso_estimator__alpha': 0.25, 'rf_estimator__n_estimators': 120},
{'lasso_estimator__alpha': 0.5, 'rf_estimator__n_estimators': 20},
{'lasso_estimator__alpha': 0.5, 'rf_estimator__n_estimators': 40},
{'lasso_estimator__alpha': 0.5, 'rf_estimator__n_estimators': 60},
{'lasso_estimator__alpha': 0.5, 'rf_estimator__n_estimators': 80},
{'lasso_estimator__alpha': 0.5, 'rf_estimator__n_estimators': 100},
{'lasso_estimator__alpha': 0.5, 'rf_estimator__n_estimators': 120},
{'lasso_estimator__alpha': 0.75, 'rf_estimator__n_estimators': 20},
{'lasso_estimator__alpha': 0.75, 'rf_estimator__n_estimators': 40},
{'lasso_estimator__alpha': 0.75, 'rf_estimator__n_estimators': 60},
{'lasso_estimator__alpha': 0.75, 'rf_estimator__n_estimators': 80},
{'lasso_estimator__alpha': 0.75, 'rf_estimator__n_estimators': 100},
{'lasso_estimator__alpha': 0.75, 'rf_estimator__n_estimators': 120},
{'lasso_estimator__alpha': 1.0, 'rf_estimator__n_estimators': 20},
{'lasso_estimator__alpha': 1.0, 'rf_estimator__n_estimators': 40},
{'lasso_estimator__alpha': 1.0, 'rf_estimator__n_estimators': 60},
{'lasso_estimator__alpha': 1.0, 'rf_estimator__n_estimators': 80},
{'lasso_estimator__alpha': 1.0, 'rf_estimator__n_estimators': 100},
{'lasso_estimator__alpha': 1.0, 'rf_estimator__n_estimators': 120},
{'lasso_estimator__alpha': 1.25, 'rf_estimator__n_estimators': 20},
{'lasso_estimator__alpha': 1.25, 'rf_estimator__n_estimators': 40},
{'lasso_estimator__alpha': 1.25, 'rf_estimator__n_estimators': 60},
{'lasso_estimator__alpha': 1.25, 'rf_estimator__n_estimators': 80},
{'lasso_estimator__alpha': 1.25, 'rf_estimator__n_estimators': 100},
{'lasso_estimator__alpha': 1.25, 'rf_estimator__n_estimators': 120},
{'lasso_estimator__alpha': 1.5, 'rf_estimator__n_estimators': 20},
{'lasso_estimator__alpha': 1.5, 'rf_estimator__n_estimators': 40},
{'lasso_estimator__alpha': 1.5, 'rf_estimator__n_estimators': 60},
{'lasso_estimator__alpha': 1.5, 'rf_estimator__n_estimators': 80},
{'lasso_estimator__alpha': 1.5, 'rf_estimator__n_estimators': 100},
{'lasso_estimator__alpha': 1.5, 'rf_estimator__n_estimators': 120}],
'split0_test_score': array([0.48765423, 0.47007607, 0.41456128, 0.34332073, 0.36888898,
0.370369 , 0.50945042, 0.52478666, 0.45136636, 0.38160909,
0.46464615, 0.52426278, 0.33309356, 0.50165501, 0.5023884 ,
0.47159884, 0.40443694, 0.42850669, 0.35280764, 0.41274937,
0.41530415, 0.35325067, 0.461381 , 0.40458056, 0.45063697,
0.47402597, 0.39203225, 0.58405673, 0.43074069, 0.36958539,
0.35946403, 0.46811327, 0.43129582, 0.47471034, 0.31616108,
0.43820558]),
'split1_test_score': array([0.31748269, 0.32402775, 0.31309735, 0.36776797, 0.36291097,
0.25860886, 0.32332546, 0.28310914, 0.34370404, 0.29429633,
0.32531769, 0.30070425, 0.32083858, 0.31018103, 0.28147265,
0.36096592, 0.33612201, 0.34993859, 0.31710402, 0.34449814,
0.32729745, 0.29203103, 0.3028285 , 0.40849055, 0.35384028,
0.35159579, 0.30777994, 0.34548216, 0.29892216, 0.32126091,
0.30904616, 0.30511572, 0.30571425, 0.356684 , 0.32693294,
0.33647908]),
'split2_test_score': array([0.36714477, 0.28075098, 0.27797057, 0.28236282, 0.30276893,
0.21700352, 0.38350757, 0.3370075 , 0.31649401, 0.20121556,
0.30713851, 0.28664918, 0.33362753, 0.30618393, 0.36897318,
0.24307011, 0.33060169, 0.32188143, 0.35355399, 0.32021347,
0.35526908, 0.25476369, 0.26570208, 0.16455204, 0.4154126 ,
0.30368747, 0.27953113, 0.32737498, 0.23057391, 0.31069444,
0.36235946, 0.2807269 , 0.33147417, 0.2414187 , 0.2822582 ,
0.24876048]),
'split3_test_score': array([0.4043803 , 0.31910819, 0.23721216, 0.30117822, 0.24160984,
0.29643875, 0.29444929, 0.36670958, 0.29294625, 0.35849669,
0.28732813, 0.06164115, 0.27354921, 0.30412114, 0.31082146,
0.23641828, 0.29371034, 0.34239524, 0.39866027, 0.36307616,
0.2895736 , 0.31561043, 0.41537819, 0.25744729, 0.39204788,
0.35827202, 0.3558286 , 0.25123577, 0.22871596, 0.36031404,
0.33534641, 0.31542919, 0.29505816, 0.30829603, 0.27520299,
0.20069686]),
'split4_test_score': array([0.37299925, 0.29360033, 0.35534609, 0.34508877, 0.3955746 ,
0.24485609, 0.32355244, 0.40128887, 0.25337656, 0.26202744,
0.2442764 , 0.12475539, 0.36143398, 0.25855855, 0.27470568,
0.37247721, 0.26957179, 0.28886332, 0.34711816, 0.35216452,
0.30793447, 0.26319255, 0.22076315, 0.197187 , 0.29571515,
0.30295817, 0.27574516, 0.32196883, 0.32617658, 0.23406369,
0.30742707, 0.37246999, 0.1981131 , 0.35704234, 0.26689645,
0.29602189]),
'mean_test_score': array([0.38993225, 0.33751266, 0.31963749, 0.3279437 , 0.33435067,
0.27745524, 0.36685703, 0.38258035, 0.33157744, 0.29952902,
0.32574138, 0.25960255, 0.32450857, 0.33613993, 0.34767227,
0.33690607, 0.32688855, 0.34631705, 0.35384882, 0.35854033,
0.33907575, 0.29576967, 0.33321058, 0.28645149, 0.38153057,
0.35810788, 0.32218342, 0.3660237 , 0.30302586, 0.31918369,
0.33472862, 0.34837101, 0.3123311 , 0.34763028, 0.29349033,
0.30403278]),
'std_test_score': array([0.05623747, 0.06818182, 0.06141412, 0.03133811, 0.05541701,
0.05303893, 0.07697179, 0.0809888 , 0.06683068, 0.06528952,
0.07450222, 0.16114489, 0.02874254, 0.08486524, 0.08420844,
0.08819219, 0.04582314, 0.04622048, 0.0260949 , 0.03054825,
0.04389069, 0.03592898, 0.09088902, 0.10248598, 0.05322657,
0.06242197, 0.04515318, 0.11364082, 0.07434396, 0.04807043,
0.0235824 , 0.06700877, 0.0747087 , 0.07635179, 0.02366514,
0.08105877]),
'rank_test_score': array([ 1, 14, 26, 21, 18, 35, 4, 2, 20, 31, 23, 36, 24, 16, 10, 15, 22,
12, 8, 6, 13, 32, 19, 34, 3, 7, 25, 5, 30, 27, 17, 9, 28, 11,
33, 29])}
import numpy
from mpl_toolkits.mplot3d import Axes3D
import matplotlib.pyplot as plt
fig = plt.figure(figsize=(14, 6))
ax = fig.add_subplot(131, projection='3d')
xs = numpy.array([el['lasso_estimator__alpha'] for el in grid.cv_results_['params']])
ys = numpy.array([el['rf_estimator__n_estimators'] for el in grid.cv_results_['params']])
zs = numpy.array(grid.cv_results_['mean_test_score'])
ax.scatter(xs, ys, zs)
ax.set_title("3D...")
ax = fig.add_subplot(132)
for x in sorted(set(xs)):
y2 = ys[xs == x]
z2 = zs[xs == x]
ax.plot(y2, z2, label="alpha=%1.2f" % x, lw=x*2)
ax.legend();
ax = fig.add_subplot(133)
for y in sorted(set(ys)):
x2 = xs[ys == y]
z2 = zs[ys == y]
ax.plot(x2, z2, label="n_estimators=%d" % y, lw=y/40)
ax.legend();
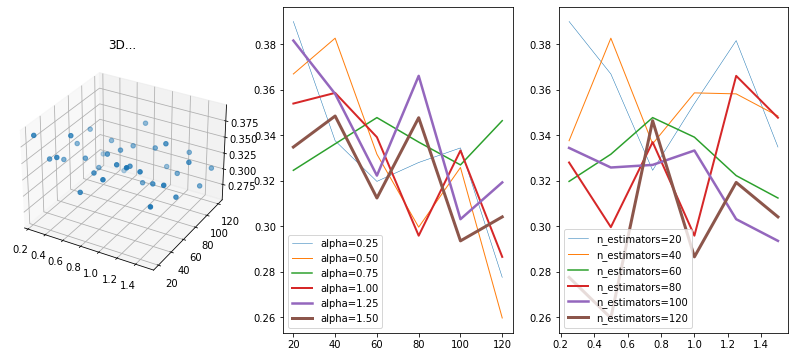
Il semble que la valeur de alpha importe peu mais qu’un grand nombre d’arbres a un impact positif. Cela dit, il faut ne pas oublier l’écart-type de ces variations qui n’est pas négligeable.