1A.1 - Variables, boucles, tests (correction)#

Links: notebook, html, python, slides, GitHub

Boucles, tests, correction.

from jyquickhelper import add_notebook_menu
add_notebook_menu()

Partie 3 : boucles (exercice)#

l = [ 4, 3, 0, 2, 1 ]
i = 0
while l[i] != 0 :
    i = l[i]
    print (i)            # que vaut l[i] à la fin ?

4
1
3
2

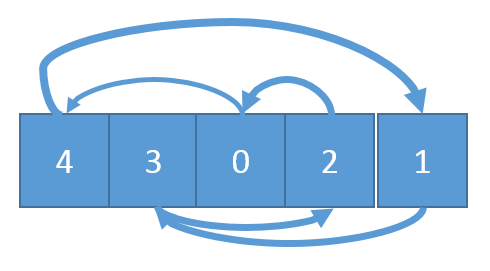
Cet exercice montre une façon curieuse de se déplacer dans un tableau puisqu’on commence à la première position puis on va la position indiqué par le premier élément du tableau et ainsi de suite. On s’arrête quand on tombe sur la valeur zéro.

from IPython.display import Image
Image("td2_1.png")
../_images/td1a_correction_session2_5_0.png

Partie 5 : recherche non dichotomique (exercice)#

Il n’y a pas d’autres moyens que de passer tous les éléments en revue et de conserver la position du premier élément dans la liste qui vérifie le critère de recherche.

l = [ 3, 6, 2 , 7, 9 ]
x = 7

for i,v in enumerate(l) :
    if v == x :
        position = i

print ( position )

3

Partie 6 : recherche dichotomique (exercice)#

La recherche dichotomique s’applique uniquement sur un tableau triée. A chaque itération, on vise le milieu du tableau pour savoir dans quelle moitié chercher.

l = [2, 3, 6, 7, 9]
# si la liste n'est pas triée, il faut écrire :
l.sort ()
x = 7

a = 0
b = len(l)-1
while a <= b :
    m = (a+b)//2  # ne pas oublier // sinon la division est réelle
    if l[m] == x :
        position = m   # ligne A
        break          # pas la peine de continuer, on quitte la boucle
    elif l[m] < x :
        a = m+1
    else :
        b = m-1

print ( position )

3

Partie 7 : pour aller plus loin (exercice)#

Lorsque l’élément à chercher n’est pas dans la liste, cela déclenche une erreur :

l = [2, 3, 6, 7, 9]
l.sort ()
x = 5

position = -1

a = 0
b = len(l)-1
while a <= b :
    m = (a+b)//2
    if l[m] == x :
        position = m
        break
    elif l[m] < x :
        a = m+1
    else :
        b = m-1

print ( position )

None

Le programme affiche None qui était la valeur par défaut de la variable position. La boucle n’a pas changé le contenu de la variable. Donc, lorsque position==-1, cela veut dire que le résultat n’a pas été trouvé.

Coût

Comme à chaque itération, on divise la taille du problème par deux, on est sûr que l’algorithme a trouvé la réponse lorsque \frac{n}{2^k} < 1 où n est le nombre d’éléments du tableau et k le nombre d’itérations. Par conséquent, k \sim \ln_2 n. On note cela O(\ln_2 n). Le programme suivant vérifie cela :

import random, math
l = list(range(0,1000000))

for k in range(0,10):
    x = random.randint(0,l[-1])

    iter = 0
    a = 0
    b = len(l)-1
    while a <= b :
        iter += 1
        m = (a+b)//2
        if l[m] == x :
            position = m
            break
        elif l[m] < x :
            a = m+1
        else :
            b = m-1

    print ("k=",k, "x=", x, "itération=", iter, " log2(len(l))=", math.log(len(l))/math.log(2))

k= 0 x= 298775 itération= 20  log2(len(l))= 19.931568569324174
k= 1 x= 941582 itération= 19  log2(len(l))= 19.931568569324174
k= 2 x= 74686 itération= 20  log2(len(l))= 19.931568569324174
k= 3 x= 274574 itération= 20  log2(len(l))= 19.931568569324174
k= 4 x= 573574 itération= 20  log2(len(l))= 19.931568569324174
k= 5 x= 351579 itération= 18  log2(len(l))= 19.931568569324174
k= 6 x= 414944 itération= 20  log2(len(l))= 19.931568569324174
k= 7 x= 556908 itération= 20  log2(len(l))= 19.931568569324174
k= 8 x= 894863 itération= 19  log2(len(l))= 19.931568569324174
k= 9 x= 651824 itération= 20  log2(len(l))= 19.931568569324174