2A.data - DataFrame et Graphes - correction#

Links: notebook, html, python, slides, GitHub

Opérations standards sur les dataframes (pandas) et les matrices (numpy). Graphiques avec matplotlib).

%matplotlib inline
import matplotlib.pyplot as plt

from jyquickhelper import add_notebook_menu
add_notebook_menu()

Exercice 1 : créer un fichier Excel

On souhaite récupérer les données donnees_enquete_2003_television.txt (source : INSEE).

POIDSLOG : Pondération individuelle relative
POIDSF : Variable de pondération individuelle
cLT1FREQ : Nombre d’heures en moyenne passées à regarder la télévision
cLT2FREQ : Unité de temps utilisée pour compter le nombre d’heures passées à regarder la télévision, cette unité est représentée par les quatre valeurs suivantes
- 0 : non concerné
- 1 : jour
- 2 : semaine
- 3 : mois

Ensuite, on veut :

Supprimer les colonnes vides
Obtenir les valeurs distinctes pour la colonne cLT2FREQ
Modifier la matrice pour enlever les lignes pour lesquelles l’unité de temps (cLT2FREQ) n’est pas renseignée ou égale à zéro.
Sauver le résultat au format Excel.

Vous aurez peut-être besoin des fonctions suivantes :

import pandas
from ensae_teaching_cs.data import donnees_enquete_2003_television
df = pandas.read_csv(donnees_enquete_2003_television(), sep="\t", engine="python")
df.head()

	POIDLOG	POIDSF	cLT1FREQ	cLT2FREQ	Unnamed: 4	Unnamed: 5	Unnamed: 6	Unnamed: 7	Unnamed: 8	Unnamed: 9	...	Unnamed: 22	Unnamed: 23	Unnamed: 24	Unnamed: 25	Unnamed: 26	Unnamed: 27	Unnamed: 28	Unnamed: 29	Unnamed: 30	Unnamed: 31
0	0.889422	4766.865201	2	1.0	NaN	NaN	NaN	NaN	NaN	NaN	...	NaN	NaN	NaN	NaN	NaN	NaN	NaN	NaN	NaN	NaN
1	2.310209	12381.589746	30	1.0	NaN	NaN	NaN	NaN	NaN	NaN	...	NaN	NaN	NaN	NaN	NaN	NaN	NaN	NaN	NaN	NaN
2	2.740070	14685.431344	6	2.0	NaN	NaN	NaN	NaN	NaN	NaN	...	NaN	NaN	NaN	NaN	NaN	NaN	NaN	NaN	NaN	NaN
3	1.775545	9516.049939	1	1.0	NaN	NaN	NaN	NaN	NaN	NaN	...	NaN	NaN	NaN	NaN	NaN	NaN	NaN	NaN	NaN	NaN
4	0.732512	3925.907588	3	1.0	NaN	NaN	NaN	NaN	NaN	NaN	...	NaN	NaN	NaN	NaN	NaN	NaN	NaN	NaN	NaN	NaN

5 rows × 32 columns

On enlève les colonnes vides :

df = df [[ c for c in df.columns if "Unnamed" not in c]]
df.head()

	POIDLOG	POIDSF	cLT1FREQ	cLT2FREQ
0	0.889422	4766.865201	2	1.0
1	2.310209	12381.589746	30	1.0
2	2.740070	14685.431344	6	2.0
3	1.775545	9516.049939	1	1.0
4	0.732512	3925.907588	3	1.0

notnull = df [ ~df.cLT2FREQ.isnull() ]  # équivalent )  df [ df.cLT2FREQ.notnull() ]
print(len(df),len(notnull))
notnull.tail()

8403 7386

	POIDLOG	POIDSF	cLT1FREQ	cLT2FREQ
8397	0.502091	2690.961176	3	1.0
8398	0.306852	1644.574141	6	1.0
8399	2.501181	13405.104689	6	1.0
8400	1.382758	7410.905653	1	1.0
8401	0.343340	1840.132652	3	1.0

notnull.to_excel("data.xlsx")  # question 4

Pour lancer Excel, vous pouvez juste écrire ceci :

%system "data.xlsx"

[]

Vous devriez voir quelque chose comme ceci :

from IPython.display import Image
Image("td10exc.png")

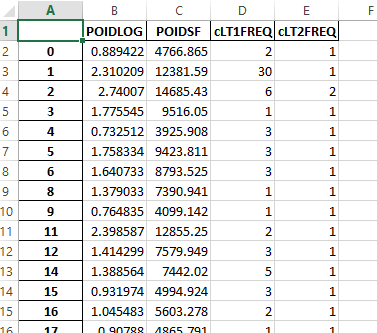
../_images/td2a_correction_session_1_12_0.png

Questions

Que changerait l’ajout du paramètre ``how=”outer”`` dans ce cas ?
On cherche à joindre deux tables A,B qui ont chacune trois clés distinctes : :math:`c_1, c_2, c_3`. Il y a respectivement dans chaque table :math:`A_i` et :math:`B_i` lignes pour la clé :math:`c_i`. Combien la table finale issue de la fusion des deux tables contiendra-t-elle de lignes ?

L’ajout du paramètres how='outer' ne changerait rien dans ce cas car les deux tables fusionnées contiennent exactement les mêmes clés.

Le nombre de lignes obtenus serait $\sum_{i=1}^{3} A_i B_i$ . Il y a trois clés, chaque ligne de la table A doit être associée à toutes les lignes de la table B partageant la même clé.

Exercice 2 : lambda fonction

Ecrire une lambda fonction qui prend deux paramètres et qui est équivalente à la fonction suivante :

def delta(x,y):
    return max(x,y)- min(x,y)

delta = lambda x,y : max(x,y)- min(x,y)

delta(4,5)

import random
df["select"]= df.apply( lambda row : random.randint(1,10), axis=1)
echantillon = df [ df["select"] ==1 ]
echantillon.shape, df.shape

((851, 5), (8403, 5))

Exercice 3 : moyennes par groupes

Toujours avec le même jeu de données (marathon.txt), on veut ajouter une ligne à la fin du tableau croisé dynamique contenant la moyenne en secondes des temps des marathons pour chaque ville.

from ensae_teaching_cs.data import marathon
import pandas
df = pandas.read_csv(marathon(), sep="\t", names=["ville", "annee", "temps","secondes"])
df.head()

	ville	annee	temps	secondes
0	PARIS	2011	02:06:29	7589
1	PARIS	2010	02:06:41	7601
2	PARIS	2009	02:05:47	7547
3	PARIS	2008	02:06:40	7600
4	PARIS	2007	02:07:17	7637

La solution requiert trois étapes.

Pour avoir la moyenne par villes, il faut grouper les lignes associées à la même villes.
Ensuite, il faut introduire ces moyennes dans la table initiale : on fusionne.
On effectue le même pivot que dans l’énoncé.

# étape 1
# par défaut, la méthode groupby utilise la clé de group comme index
# pour ne pas le faire, il faut préciser as_index = False
gr = df[["ville","secondes"]].groupby("ville", as_index=False).mean()
gr.head()

	ville	secondes
0	AMSTERDAM	7883.371429
1	BERLIN	7922.315789
2	BOSTON	7891.061224
3	CHICAGO	7815.909091
4	FUKUOKA	8075.187500

# étape 2 - on ajoute une colonne
tout = df.merge( gr, on="ville")
tout.head()

	ville	annee	temps	secondes_x	secondes_y
0	PARIS	2011	02:06:29	7589	7937.028571
1	PARIS	2010	02:06:41	7601	7937.028571
2	PARIS	2009	02:05:47	7547	7937.028571
3	PARIS	2008	02:06:40	7600	7937.028571
4	PARIS	2007	02:07:17	7637	7937.028571

# étape 3
piv = tout.pivot("annee","ville","secondes_x")
piv.tail()

ville	AMSTERDAM	BERLIN	BOSTON	CHICAGO	FUKUOKA	LONDON	NEW YORK	PARIS	STOCKOLM
annee
2007	7589.0	7466.0	8053.0	7871.0	7599.0	7661.0	7744.0	7637.0	8456.0
2008	7672.0	7439.0	7665.0	7585.0	7570.0	7515.0	7723.0	7600.0	8163.0
2009	7578.0	7568.0	7722.0	7541.0	7518.0	7510.0	7755.0	7547.0	8134.0
2010	7544.0	7508.0	7552.0	7583.0	7704.0	7519.0	7694.0	7601.0	7968.0
2011	NaN	7418.0	7382.0	NaN	NaN	7480.0	NaN	7589.0	8047.0

A partir de là, on ne voit pas trop comment s’en sortir. Voici ce que je propose :

On effectue un pivot sur la petite matrice des moyennes.
On ajoute ce second pivot avec le premier (celui de l’énoncé).

gr["annee"] = "moyenne"
pivmean = gr.pivot("annee","ville","secondes")
pivmean

ville	AMSTERDAM	BERLIN	BOSTON	CHICAGO	FUKUOKA	LONDON	NEW YORK	PARIS	STOCKOLM
annee
moyenne	7883.371429	7922.315789	7891.061224	7815.909091	8075.1875	7695.16129	7928.560976	7937.028571	8133.393939

piv = df.pivot("annee","ville","secondes")
pandas.concat( [ piv, pivmean ]).tail()

ville	AMSTERDAM	BERLIN	BOSTON	CHICAGO	FUKUOKA	LONDON	NEW YORK	PARIS	STOCKOLM
annee
2008	7672.000000	7439.000000	7665.000000	7585.000000	7570.0000	7515.00000	7723.000000	7600.000000	8163.000000
2009	7578.000000	7568.000000	7722.000000	7541.000000	7518.0000	7510.00000	7755.000000	7547.000000	8134.000000
2010	7544.000000	7508.000000	7552.000000	7583.000000	7704.0000	7519.00000	7694.000000	7601.000000	7968.000000
2011	NaN	7418.000000	7382.000000	NaN	NaN	7480.00000	NaN	7589.000000	8047.000000
moyenne	7883.371429	7922.315789	7891.061224	7815.909091	8075.1875	7695.16129	7928.560976	7937.028571	8133.393939

En résumé, cela donne (j’ajoute aussi le nombre de marathons courus) :

import pandas, urllib.request
from ensae_teaching_cs.data import marathon
df = pandas.read_csv(marathon(filename=True),
                     sep="\t", names=["ville", "annee", "temps","secondes"])
piv = df.pivot("annee","ville","secondes")
gr = df[["ville","secondes"]].groupby("ville", as_index=False).mean()
gr["annee"] = "moyenne"
pivmean = gr.pivot("annee","ville","secondes")

pandas.concat([piv, pivmean]).tail()

ville	AMSTERDAM	BERLIN	BOSTON	CHICAGO	FUKUOKA	LONDON	NEW YORK	PARIS	STOCKOLM
annee
2008	7672.000000	7439.000000	7665.000000	7585.000000	7570.0000	7515.00000	7723.000000	7600.000000	8163.000000
2009	7578.000000	7568.000000	7722.000000	7541.000000	7518.0000	7510.00000	7755.000000	7547.000000	8134.000000
2010	7544.000000	7508.000000	7552.000000	7583.000000	7704.0000	7519.00000	7694.000000	7601.000000	7968.000000
2011	NaN	7418.000000	7382.000000	NaN	NaN	7480.00000	NaN	7589.000000	8047.000000
moyenne	7883.371429	7922.315789	7891.061224	7815.909091	8075.1875	7695.16129	7928.560976	7937.028571	8133.393939

Exercice 4 : écart entre les mariés

En ajoutant une colonne et en utilisant l’opération group by, on veut obtenir la distribution du nombre de mariages en fonction de l’écart entre les mariés. Au besoin, on changera le type d’une colone ou deux.
On veut tracer un nuage de points avec en abscisse l’âge du mari, en ordonnée, l’âge de la femme. Il faudra peut-être jeter un coup d’oeil sur la documentation de la méthode plot.

import urllib.request
import zipfile
import http.client

def download_and_save(name, root_url):
    try:
        response = urllib.request.urlopen(root_url+name)
    except (TimeoutError, urllib.request.URLError, http.client.BadStatusLine):
        # back up plan
        root_url = "http://www.xavierdupre.fr/enseignement/complements/"
        response = urllib.request.urlopen(root_url+name)
    with open(name, "wb") as outfile:
        outfile.write(response.read())

def unzip(name):
    with zipfile.ZipFile(name, "r") as z:
        z.extractall(".")

filenames = ["etatcivil2012_mar2012_dbase.zip",
             "etatcivil2012_nais2012_dbase.zip",
             "etatcivil2012_dec2012_dbase.zip", ]
root_url = 'http://telechargement.insee.fr/fichiersdetail/etatcivil2012/dbase/'

for filename in filenames:
    download_and_save(filename, root_url)
    unzip(filename)
    print("Download of {}: DONE!".format(filename))

Download of etatcivil2012_mar2012_dbase.zip: DONE!
Download of etatcivil2012_nais2012_dbase.zip: DONE!
Download of etatcivil2012_dec2012_dbase.zip: DONE!

import pandas
try:
    from dbfread_ import DBF
    use_dbfread = True
except ImportError as e :
    use_dbfread = False

if use_dbfread:
    print("use of dbfread")
    def dBase2df(dbase_filename):
        table = DBF(dbase_filename, load=True, encoding="cp437")
        return pandas.DataFrame(table.records)

    df = dBase2df('mar2012.dbf')
else :
    print("use of zipped version")
    import pyensae.datasource
    data = pyensae.datasource.download_data("mar2012.zip")
    df = pandas.read_csv(data[0], sep="\t", encoding="utf8", low_memory=False)

print(df.shape, df.columns)
df.head()

use of zipped version
(246123, 16) Index(['AMAR', 'ANAISF', 'ANAISH', 'DEPDOM', 'DEPMAR', 'DEPNAISF', 'DEPNAISH',
       'ETAMATF', 'ETAMATH', 'INDNATF', 'INDNATH', 'JSEMAINE', 'MMAR',
       'NBENFCOM', 'TUCOM', 'TUDOM'],
      dtype='object')

	AMAR	ANAISF	ANAISH	DEPDOM	DEPMAR	DEPNAISF	DEPNAISH	ETAMATF	ETAMATH	INDNATF	INDNATH	JSEMAINE	MMAR	NBENFCOM	TUCOM	TUDOM
0	2012	1984	1982	99	29	99	75	1	1	2	1	1	1	N	NaN	9
1	2012	1969	1956	99	75	99	69	4	4	2	2	3	1	N	NaN	9
2	2012	1992	1982	99	34	99	99	1	1	1	2	5	1	N	NaN	9
3	2012	1987	1985	99	13	84	99	1	1	1	2	4	1	N	NaN	9
4	2012	1963	1968	99	26	99	99	1	1	2	2	6	1	N	NaN	9

df["ageH"] = df.apply (lambda r:  2014 - int(r["ANAISH"]), axis=1)
df["ageF"] = df.apply (lambda r:  2014 - int(r["ANAISF"]), axis=1)
df.head()

	AMAR	ANAISF	ANAISH	DEPDOM	DEPMAR	DEPNAISF	DEPNAISH	ETAMATF	ETAMATH	INDNATF	INDNATH	JSEMAINE	MMAR	NBENFCOM	TUCOM	TUDOM	ageH	ageF
0	2012	1984	1982	99	29	99	75	1	1	2	1	1	1	N	NaN	9	32	30
1	2012	1969	1956	99	75	99	69	4	4	2	2	3	1	N	NaN	9	58	45
2	2012	1992	1982	99	34	99	99	1	1	1	2	5	1	N	NaN	9	32	22
3	2012	1987	1985	99	13	84	99	1	1	1	2	4	1	N	NaN	9	29	27
4	2012	1963	1968	99	26	99	99	1	1	2	2	6	1	N	NaN	9	46	51

df.plot(x="ageH",y="ageF", kind="scatter")

<matplotlib.axes._subplots.AxesSubplot at 0x2ee646da358>

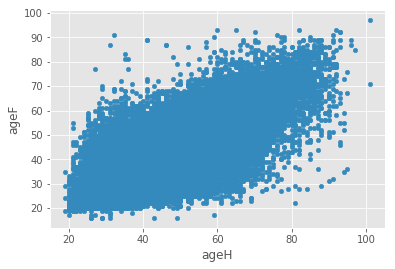
../_images/td2a_correction_session_1_35_1.png

df.plot(x="ageH",y="ageF", kind="hexbin")

<matplotlib.axes._subplots.AxesSubplot at 0x2ee6591b780>

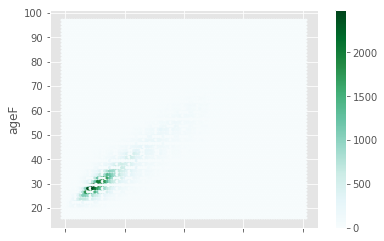
../_images/td2a_correction_session_1_36_1.png

Exercice 5 : graphe de la distribution avec pandas

Le module pandas propose un panel de graphiques standard faciles à obtenir. On souhaite représenter la distribution sous forme d’histogramme. A vous de choisir le meilleure graphique depuis la page Visualization.

df["ANAISH"] = df.apply (lambda r:  int(r["ANAISH"]), axis=1)
df["ANAISF"] = df.apply (lambda r:  int(r["ANAISF"]), axis=1)
df["differenceHF"] = df.ANAISH - df.ANAISF
df["nb"] = 1
dist = df[["nb","differenceHF"]].groupby("differenceHF", as_index=False).count()
df["differenceHF"].hist(figsize=(16,6), bins=50)

<matplotlib.axes._subplots.AxesSubplot at 0x2ee656d7c88>

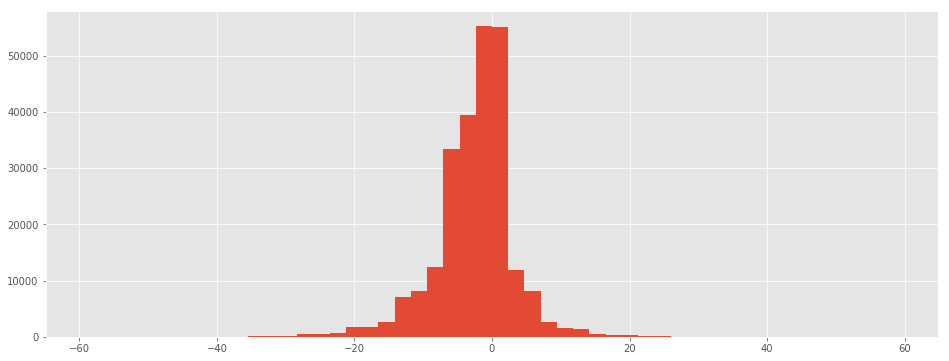
../_images/td2a_correction_session_1_38_1.png

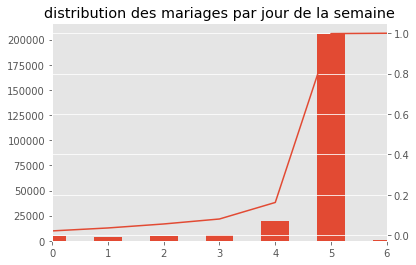
Exercice 6 : distribution des mariages par jour

On veut obtenir un graphe qui contient l’histogramme de la distribution du nombre de mariages par jour de la semaine et d’ajouter une seconde courbe correspond avec un second axe à la répartition cumulée.

df["nb"] = 1
dissem = df[["JSEMAINE","nb"]].groupby("JSEMAINE",as_index=False).sum()
total = dissem["nb"].sum()
repsem = dissem.cumsum()
repsem["nb"] /= total

ax = dissem["nb"].plot(kind="bar")
repsem["nb"].plot(ax=ax, secondary_y=True)
ax.set_title("distribution des mariages par jour de la semaine")

<matplotlib.text.Text at 0x2ee65958860>

../_images/td2a_correction_session_1_40_1.png

Liens

Contenu

Information

Sujet précédent

Sujet suivant