2A.ml - Machine Learning et Marketting - correction

Links: notebook, html, python, slides, GitHub

Classification binaire, correction.

%matplotlib inline

Populating the interactive namespace from numpy and matplotlib

import matplotlib.pyplot as plt

from jyquickhelper import add_notebook_menu
add_notebook_menu()

Données

Tout d’abord, on récupère la base de données : Bank Marketing Data Set.

url = "https://archive.ics.uci.edu/ml/machine-learning-databases/00222/"
file = "bank.zip"
import pyensae.datasource
data = pyensae.datasource.download_data(file, website=url)

import pandas
df = pandas.read_csv("bank.csv",sep=";")
df.tail()

	age	job	marital	education	default	balance	housing	loan	contact	day	month	duration	campaign	pdays	previous	poutcome	y
4516	33	services	married	secondary	no	-333	yes	no	cellular	30	jul	329	5	-1	0	unknown	no
4517	57	self-employed	married	tertiary	yes	-3313	yes	yes	unknown	9	may	153	1	-1	0	unknown	no
4518	57	technician	married	secondary	no	295	no	no	cellular	19	aug	151	11	-1	0	unknown	no
4519	28	blue-collar	married	secondary	no	1137	no	no	cellular	6	feb	129	4	211	3	other	no
4520	44	entrepreneur	single	tertiary	no	1136	yes	yes	cellular	3	apr	345	2	249	7	other	no

Exercice 1 : prédire y en fonction des attributs

Les données ne sont pas toutes au format numérique, il faut convertir les variables catégorielles. Pour cela, on utilise la fonction DictVectorizer.

import numpy
import numpy as np
numerique = [ c for c,d in zip(df.columns,df.dtypes) if d == numpy.int64 ]
categories = [ c for c in df.columns if c not in numerique and c not in ["y"] ]
target = "y"
print(numerique)
print(categories)
print(target)
num = df[ numerique ]
cat = df[ categories ]
tar = df[ target ]

['age', 'balance', 'day', 'duration', 'campaign', 'pdays', 'previous']
['job', 'marital', 'education', 'default', 'housing', 'loan', 'contact', 'month', 'poutcome']
y

On traite les variables catégorielles :

from sklearn.feature_extraction import DictVectorizer
prep = DictVectorizer()
cat_as_dicts = [dict(r.iteritems()) for _, r in cat.iterrows()]
temp = prep.fit_transform(cat_as_dicts)
cat_exp = temp.toarray()
prep.feature_names_

['contact=cellular',
 'contact=telephone',
 'contact=unknown',
 'default=no',
 'default=yes',
 'education=primary',
 'education=secondary',
 'education=tertiary',
 'education=unknown',
 'housing=no',
 'housing=yes',
 'job=admin.',
 'job=blue-collar',
 'job=entrepreneur',
 'job=housemaid',
 'job=management',
 'job=retired',
 'job=self-employed',
 'job=services',
 'job=student',
 'job=technician',
 'job=unemployed',
 'job=unknown',
 'loan=no',
 'loan=yes',
 'marital=divorced',
 'marital=married',
 'marital=single',
 'month=apr',
 'month=aug',
 'month=dec',
 'month=feb',
 'month=jan',
 'month=jul',
 'month=jun',
 'month=mar',
 'month=may',
 'month=nov',
 'month=oct',
 'month=sep',
 'poutcome=failure',
 'poutcome=other',
 'poutcome=success',
 'poutcome=unknown']

On construit les deux matrices = (features, classe).

Remarque : certains modèles d’apprentissage n’acceptent pas les corrélations. Lorsqu’on crée des variables catégorielles à choix unique, les sommes des colonnes associées à une catégories fait nécessairement un. Avec deux variables catégorielles, on introduit nécessairement des corrélations. On pense à enlever les dernières catégories : 'contact=unknown', 'default=yes', 'education=unknown', 'housing=yes', 'job=unknown', 'loan=yes', 'marital=single', 'month=sep', 'poutcome=unknown'.

cat_exp_df = pandas.DataFrame( cat_exp, columns = prep.feature_names_ )
reject = ['contact=unknown', 'default=yes', 'education=unknown', 'housing=yes','job=unknown',
          'loan=yes', 'marital=single', 'month=sep', 'poutcome=unknown']
keep = [ c for c in cat_exp_df.columns if c not in reject ]
cat_exp_df_nocor = cat_exp_df [ keep ]
X = pandas.concat ( [ num, cat_exp_df_nocor ], axis= 1)
Y = tar.apply( lambda r : (1.0 if r == "yes" else 0.0))
X.shape, Y.shape

((4521, 42), (4521,))

Quelques corrélations sont très grandes malgré tout :

import numpy
numpy.corrcoef(X)

array([[ 1.        ,  0.99733687,  0.96756321, ...,  0.89646012,
         0.9809934 ,  0.94772372],
       [ 0.99733687,  1.        ,  0.98202501, ...,  0.8917544 ,
         0.99153146,  0.96013301],
       [ 0.96756321,  0.98202501,  1.        , ...,  0.90132068,
         0.998155  ,  0.98697606],
       ...,
       [ 0.89646012,  0.8917544 ,  0.90132068, ...,  1.        ,
         0.90491984,  0.94963638],
       [ 0.9809934 ,  0.99153146,  0.998155  , ...,  0.90491984,
         1.        ,  0.98331872],
       [ 0.94772372,  0.96013301,  0.98697606, ...,  0.94963638,
         0.98331872,  1.        ]])

On divise en base d’apprentissage et de test :

from sklearn.model_selection import train_test_split
X_train, X_test, Y_train, Y_test = train_test_split(X, Y, test_size=0.33)

Puis on cale un modèle d’apprentissage :

from sklearn.ensemble import GradientBoostingClassifier, RandomForestClassifier
type_classifier = GradientBoostingClassifier
clf = type_classifier()
clf = clf.fit(X_train, Y_train.ravel())

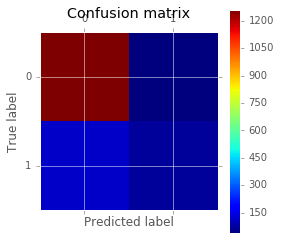
La méthode ravel évite de prendre en compte l’index de Y_train. La méthode train_test_split conserve dans l’index les positions initiales des élèments. Mais l’index fait que Y_train[0] ne désigne pas le premier élément de Y_train mais le premier élément du tableau initial. Y_train.ravel()[0] désigne bien le premier élément du tableau. On calcule ensuite la matrice de confusion (Confusion matrix) :

from sklearn.metrics import confusion_matrix
for x,y in [ (X_train, Y_train), (X_test, Y_test) ]:
    yp  = clf.predict(x)
    cm = confusion_matrix(y.ravel(), yp.ravel())
    print(cm)

import matplotlib.pyplot as plt
plt.matshow(cm)
plt.title('Confusion matrix')
plt.colorbar()
plt.ylabel('True label')
plt.xlabel('Predicted label')

[[2685   14]
 [ 161  169]]
[[1261   40]
 [ 120   71]]

<matplotlib.text.Text at 0x294ed68>

Si le model choisi est un GradientBoostingClassifier, on peut regarder l’importance des variables dans la construction du résultat. Le graphe suivant est inspiré de la page Gradient Boosting regression même si ce n’est pas une régression qui a été utilisée ici.

import numpy as np
feature_name = X.columns

limit = 20
feature_importance = clf.feature_importances_[:20]
feature_importance = 100.0 * (feature_importance / feature_importance.max())
sorted_idx = np.argsort(feature_importance)
pos = np.arange(sorted_idx.shape[0]) + .5
plt.subplot(1, 2, 2)
plt.barh(pos, feature_importance[sorted_idx], align='center')
plt.yticks(pos, feature_name[sorted_idx])
plt.xlabel('Relative Importance')
plt.title('Variable Importance')

<matplotlib.text.Text at 0x149d5a90>

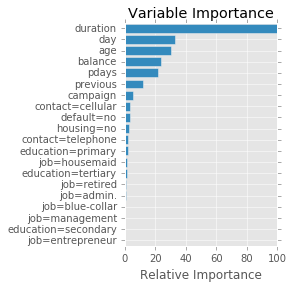
Il faut tout de même rester prudent quant à l’interprétation du graphe précédent. La documentation au sujet de limportance des features précise plus ou moins comment sont calculés ces chiffres. Toutefois, lorsque des variables sont très corrélées, elles sont plus ou moins interchangeables. Tout dépend alors comment l’algorithme d’apprentissage choisit telle ou telle variables, toujours dans le même ordre ou dans un ordre aléatoire.

variables

On utilise le code de la séance 3 Analyse en Composantes Principales pour observer les variables.

from sklearn.decomposition import PCA
pca = PCA(n_components=4)
x_transpose = X.T
pca.fit(x_transpose)

PCA(copy=True, n_components=4, whiten=False)

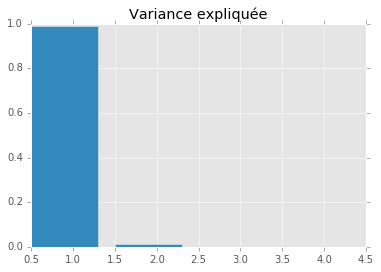
plt.bar(numpy.arange(len(pca.explained_variance_ratio_))+0.5, pca.explained_variance_ratio_)
plt.title("Variance expliquée")

<matplotlib.text.Text at 0x161b9630>

import warnings
warnings.filterwarnings('ignore')
X_reduced = pca.transform(x_transpose)
plt.figure(figsize=(18,6))
plt.scatter(X_reduced[:, 0], X_reduced[:, 1])
for label, x, y in zip(x_transpose.index, X_reduced[:, 0], X_reduced[:, 1]):
    plt.annotate(
        label,
        xy = (x, y), xytext = (-10, 10),
        textcoords = 'offset points', ha = 'right', va = 'bottom',
        bbox = dict(boxstyle = 'round,pad=0.5', fc = 'yellow', alpha = 0.5),
        arrowprops = dict(arrowstyle = '->', connectionstyle = 'arc3,rad=0'))

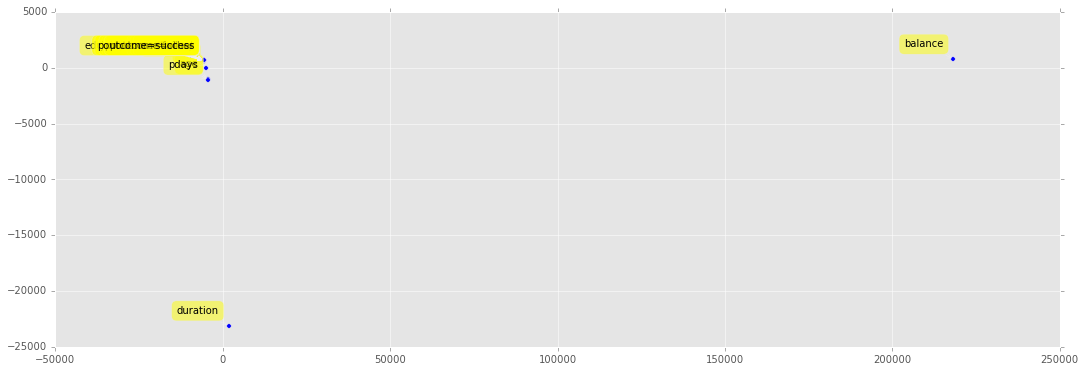
Les variables les plus dissemblables sont celles qui contribuent le plus. Toutefois, à la vue de ce graphique, il apparaît qu’il faut normaliser les données avant d’interpréter l’ACP :

from sklearn.preprocessing import normalize
xnorm = normalize(x_transpose)
pca = PCA(n_components=10)
pca.fit(xnorm)
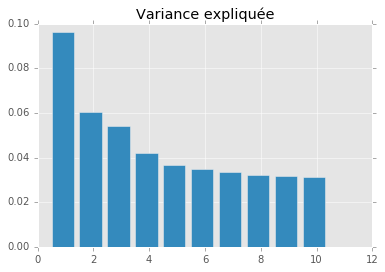
plt.bar(numpy.arange(len(pca.explained_variance_ratio_))+0.5, pca.explained_variance_ratio_)
plt.title("Variance expliquée")

<matplotlib.text.Text at 0x1628bd68>

X_reduced = pca.transform(xnorm)
plt.figure(figsize=(18,6))
plt.scatter(X_reduced[:, 0], X_reduced[:, 1])
for label, x, y in zip(x_transpose.index, X_reduced[:, 0], X_reduced[:, 1]):
    plt.annotate(
        label,
        xy = (x, y), xytext = (-10, 10),
        textcoords = 'offset points', ha = 'right', va = 'bottom',
        bbox = dict(boxstyle = 'round,pad=0.5', fc = 'yellow', alpha = 0.5),
        arrowprops = dict(arrowstyle = '->', connectionstyle = 'arc3,rad=0'))

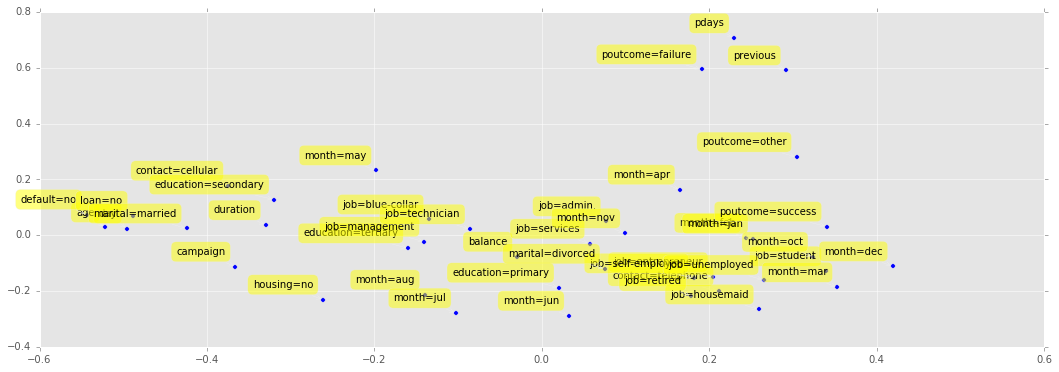
Nettement mieux. En règle générale, il est préférable de normaliser ses données avant d’apprendre un modèle. Cela n’est pas toujours nécessaire (comme pour les arbres de décision). Toutefois, numériquement, avoir des données d’ordre de grandeur très différent introduit toujours plus d’approximations.

from sklearn.pipeline import Pipeline
from sklearn.preprocessing import Normalizer
from sklearn.ensemble import GradientBoostingClassifier

clf = Pipeline([
      ('normalize', Normalizer()),
      ('classification', GradientBoostingClassifier())
    ])
clf = clf.fit(X_train, Y_train.ravel())

from sklearn.metrics import confusion_matrix
x,y = X_test, Y_test
yp  = clf.predict(x)
cm2 = confusion_matrix(y, yp)
print("non normalisé\n",cm)
print("normalisé\n",cm2)

non normalisé
 [[1261   40]
 [ 120   71]]
normalisé
 [[1270   31]
 [ 127   64]]

C’est plus ou moins équivalent lorsque les variables sont normalisées dans ce cas. Il faudrait vérifier sur la courbe ROC.

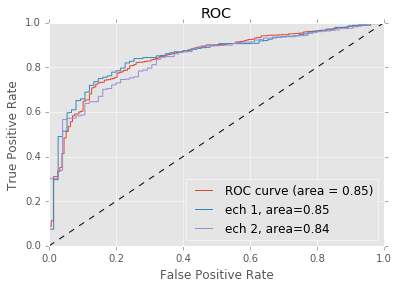
Exercice 2 : tracer la courbe ROC

On utilise l’exemple Receiver Operating Characteristic (ROC) qu’il faut modifié car la réponse juste dans notre cas est le fait de prédire la bonne classe. Cela veut dire qu’il y a deux cas pour lesquels le modèle prédit le bon résultat : on choisit la classe qui la probabilité la plus forte.

from sklearn.metrics import roc_curve, auc
probas = clf.predict_proba(X_test)
probas[:5]

array([[ 0.9792842 ,  0.0207158 ],
       [ 0.98228488,  0.01771512],
       [ 0.83708208,  0.16291792],
       [ 0.98675536,  0.01324464],
       [ 0.98818146,  0.01181854]])

On construit le vecteur des bonnes réponses :

rep = [ ]
yt = Y_test.ravel()
for i in range(probas.shape[0]):
    p0,p1 = probas[i,:]
    exp = yt[i]
    if p0 > p1 :
        if exp == 0 :
            # bonne réponse
            rep.append ( (1, p0) )
        else :
            # mauvaise réponse
            rep.append( (0,p0) )
    else :
        if exp == 0 :
            # mauvaise réponse
            rep.append ( (0, p1) )
        else :
            # bonne réponse
            rep.append( (1,p1) )
mat_rep = numpy.array(rep)
mat_rep[:5]

array([[ 1.        ,  0.9792842 ],
       [ 1.        ,  0.98228488],
       [ 1.        ,  0.83708208],
       [ 1.        ,  0.98675536],
       [ 1.        ,  0.98818146]])

"taux de bonne réponse",sum(mat_rep[:,0]/len(mat_rep)) # voir matrice de confusion

('taux de bonne réponse', 0.89410187667560337)

fpr, tpr, thresholds = roc_curve(mat_rep[:,0], mat_rep[:, 1])
roc_auc = auc(fpr, tpr)
plt.plot(fpr, tpr, label='ROC curve (area = %0.2f)' % roc_auc)
plt.plot([0, 1], [0, 1], 'k--')
plt.xlim([0.0, 1.0])
plt.ylim([0.0, 1.0])
plt.xlabel('False Positive Rate')
plt.ylabel('True Positive Rate')
plt.title('ROC')
plt.legend(loc="lower right")

<matplotlib.legend.Legend at 0x17e0df60>

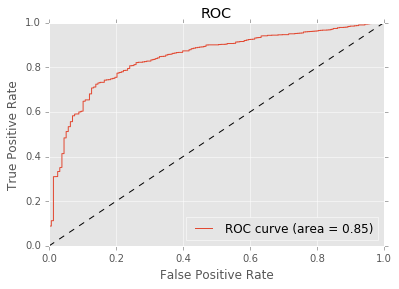
Ce score n’est pas si mal pour un premier essai. On n’a pas tenu compte du fait que la classe 1 est sous-représentée (voir Quelques astuces pour faire du machine learning. A priori, ce ne devrait pas être le cas du GradientBoostingClassifier. C’est une famille de modèles qui, lors de l’apprentissage, pondère davantage les exemples où ils font des erreurs. L’algorithme de boosting le plus connu est AdaBoost.

On tire maintenant deux échantillons aléatoires qu’on ajoute au graphique précédent :

import random
Y1 = numpy.array([ random.randint(0,1) == 0 for i in range(0,mat_rep.shape[0]) ])
Y2 = numpy.array([ random.randint(0,1) == 0 for i in range(0,mat_rep.shape[0]) ])

fpr1, tpr1, thresholds1 = roc_curve(mat_rep[Y1,0], mat_rep[Y1, 1])
roc_auc1 = auc(fpr1, tpr1)
fpr2, tpr2, thresholds2 = roc_curve(mat_rep[Y2,0], mat_rep[Y2, 1])
roc_auc2 = auc(fpr2, tpr2)
print(fpr1.shape,tpr1.shape,fpr2.shape,tpr2.shape)

import matplotlib.pyplot as plt
fig = plt.figure()
ax = fig.add_subplot(1,1,1)

ax.plot(fpr, tpr, label='ROC curve (area = %0.2f)' % roc_auc)
ax.plot([0, 1,2], [0, 1,2], 'k--')
ax.set_xlim([0.0, 1.0])
ax.set_ylim([0.0, 1.0])
ax.set_xlabel('False Positive Rate')
ax.set_ylabel('True Positive Rate')
ax.set_title('ROC')
ax.plot(fpr1, tpr1, label='ech 1, area=%0.2f' % roc_auc1)
ax.plot(fpr2, tpr2, label='ech 2, area=%0.2f' % roc_auc2)
ax.legend(loc="lower right")

(697,) (697,) (699,) (699,)

<matplotlib.legend.Legend at 0x17e82940>