Régressions linéaires avec Statsmodels et Scikit-Learn#
Links: notebook, html, python, slides, GitHub
On peut réaliser des régressions linéaires de beaucoup de manières avec Python. On en a retenu 2, statsmodels et scikit-learn. Les deux librairies ont chacunes leurs qualités et leurs défauts, sachez que l’une est plus orienté data science et l’autre plus pour des économistes.
(inspiré de la page Linear Regression with Statsmodels and Scikit-Learn)
Par exemple, statsmodel vous fournira directement le tableau de regression, pour scikit c’est moins immédiat On commence par charger tous les packages qui vont servir dans ce notebook :
from jyquickhelper import add_notebook_menu
add_notebook_menu()
%matplotlib inline
import pandas as pd
import matplotlib.pyplot as plt
import numpy as np
from scipy import stats
import seaborn as sns
import statsmodels.api as sm
from sklearn import linear_model
c:Python36_x64libsite-packagesstatsmodelscompatpandas.py:56: FutureWarning: The pandas.core.datetools module is deprecated and will be removed in a future version. Please use the pandas.tseries module instead. from pandas.core import datetools
On va utiliser la fameuse base des Iris qu’on peut appeler depuis la librairie seaborn. Pour chaque fleur, on a des informations sur la longueur et largeur de ses sépales ainsi que de ses pétales.
Pour comprendre la différence en image : Sépale.
iris = sns.load_dataset("iris")
iris.head()
| sepal_length | sepal_width | petal_length | petal_width | species | |
|---|---|---|---|---|---|
| 0 | 5.1 | 3.5 | 1.4 | 0.2 | setosa |
| 1 | 4.9 | 3.0 | 1.4 | 0.2 | setosa |
| 2 | 4.7 | 3.2 | 1.3 | 0.2 | setosa |
| 3 | 4.6 | 3.1 | 1.5 | 0.2 | setosa |
| 4 | 5.0 | 3.6 | 1.4 | 0.2 | setosa |
sns.pairplot(iris, hue="species");
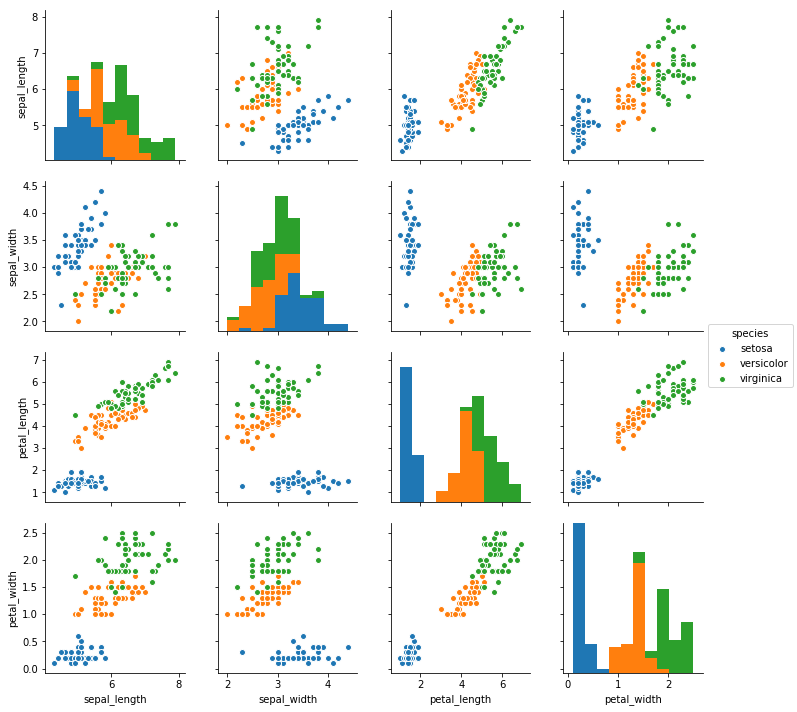
Grâce à ces graphiques, on observere une forte relation entre longeur et la largeur des pétales. On réalise une regression à une variable entre la longueur et la largeur grâce à seaborn.
Regression à une variable avec seaborn#
sns.lmplot(x="petal_length", y="petal_width", data=iris);
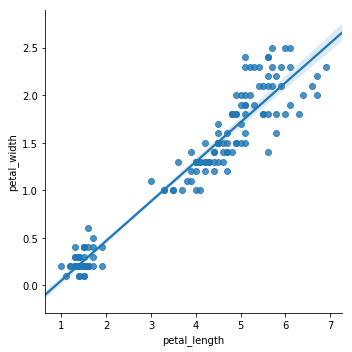
Si on observe bien qu’une relation existe, on ne connait pas grand chose d’autre.
Regression en utilisant scikit-learn#
X = iris[["petal_length"]]
y = iris["petal_width"]
# On fit le modele
model = linear_model.LinearRegression()
results = model.fit(X, y)
print(results.intercept_, results.coef_)
-0.363075521319 [ 0.41575542]
La meilleure approximation linéaire est donc y=a+bx avec - a=−0.363075521319 - b=0.41575542
Mais en termes de présentation de résultats, c’est un peu limité… Pas de
standard errors, pas de etc (du moins pas automatiquement)
Regression en utilisant statsmodels#
Remarque : on invese X et y dans la spécification du modèle pour cette librairie.
model = sm.OLS(y, X)
results = model.fit()
# Avec statsmodel, on a une sortie qui ressemble beaucoup à celle de R
print(results.summary())
OLS Regression Results
==============================================================================
Dep. Variable: petal_width R-squared: 0.967
Model: OLS Adj. R-squared: 0.967
Method: Least Squares F-statistic: 4417.
Date: Sun, 24 Sep 2017 Prob (F-statistic): 1.22e-112
Time: 20:12:37 Log-Likelihood: -8.7179
No. Observations: 150 AIC: 19.44
Df Residuals: 149 BIC: 22.45
Df Model: 1
Covariance Type: nonrobust
================================================================================
coef std err t P>|t| [0.025 0.975]
--------------------------------------------------------------------------------
petal_length 0.3365 0.005 66.463 0.000 0.327 0.347
==============================================================================
Omnibus: 19.720 Durbin-Watson: 0.857
Prob(Omnibus): 0.000 Jarque-Bera (JB): 23.498
Skew: 0.957 Prob(JB): 7.90e-06
Kurtosis: 3.311 Cond. No. 1.00
==============================================================================
Warnings:
[1] Standard Errors assume that the covariance matrix of the errors is correctly specified.
Si vous regardez de plus près, vous observez que les coefficients des deux régressions sont proches mais pas égaux. Problème de précision ? Non…
Il faut faire attention avec statsmodels, il n’inclut pas de lui-même un
intercept () alors que scikit learn le fait.
X = iris["petal_length"]
X = np.vander(X, 2) #ici on ajoute
y = iris["petal_width"]
model = sm.OLS(y, X)
results = model.fit()
print(results.summary())
OLS Regression Results
==============================================================================
Dep. Variable: petal_width R-squared: 0.927
Model: OLS Adj. R-squared: 0.927
Method: Least Squares F-statistic: 1882.
Date: Sun, 24 Sep 2017 Prob (F-statistic): 4.68e-86
Time: 20:12:37 Log-Likelihood: 24.796
No. Observations: 150 AIC: -45.59
Df Residuals: 148 BIC: -39.57
Df Model: 1
Covariance Type: nonrobust
==============================================================================
coef std err t P>|t| [0.025 0.975]
------------------------------------------------------------------------------
x1 0.4158 0.010 43.387 0.000 0.397 0.435
const -0.3631 0.040 -9.131 0.000 -0.442 -0.285
==============================================================================
Omnibus: 5.765 Durbin-Watson: 1.455
Prob(Omnibus): 0.056 Jarque-Bera (JB): 5.555
Skew: 0.359 Prob(JB): 0.0622
Kurtosis: 3.611 Cond. No. 10.3
==============================================================================
Warnings:
[1] Standard Errors assume that the covariance matrix of the errors is correctly specified.
Ca y est, les coefficients de scikit et de statsmodels sont quasi identiques (en réalité si vous regardez après la 10ème décimale, ils sont légèrement différents…)
Si on regadre le , on se dit qu’on est plutôt pas mal pour
cette régression (en même temps, dire que pour un iris, la longueur et
la largeur du pétale sont corrélées, c’est un peu normal…)’
Mais voyons si on peut aller encore plus loin, par exemple, en ajoutant l’information de l’espèce de l’iris, avec des variables catégorielles (qu’on ajoutera sous la forme d’indicatries ou dummies)
dummies = pd.get_dummies(iris["species"])
iris = pd.concat([iris, dummies], axis=1)
iris.head()
| sepal_length | sepal_width | petal_length | petal_width | species | setosa | versicolor | virginica | |
|---|---|---|---|---|---|---|---|---|
| 0 | 5.1 | 3.5 | 1.4 | 0.2 | setosa | 1 | 0 | 0 |
| 1 | 4.9 | 3.0 | 1.4 | 0.2 | setosa | 1 | 0 | 0 |
| 2 | 4.7 | 3.2 | 1.3 | 0.2 | setosa | 1 | 0 | 0 |
| 3 | 4.6 | 3.1 | 1.5 | 0.2 | setosa | 1 | 0 | 0 |
| 4 | 5.0 | 3.6 | 1.4 | 0.2 | setosa | 1 | 0 | 0 |
La regression multi-linéaire avec statsmodels#
X = iris[["petal_length", "setosa", "versicolor", "virginica"]]
X = sm.add_constant(X) # une autre façons d'ajouter une constante
y = iris["petal_width"]
model = sm.OLS(y, X)
results = model.fit()
print(results.summary())
OLS Regression Results
==============================================================================
Dep. Variable: petal_width R-squared: 0.946
Model: OLS Adj. R-squared: 0.944
Method: Least Squares F-statistic: 845.5
Date: Sun, 24 Sep 2017 Prob (F-statistic): 4.88e-92
Time: 20:12:38 Log-Likelihood: 46.704
No. Observations: 150 AIC: -85.41
Df Residuals: 146 BIC: -73.37
Df Model: 3
Covariance Type: nonrobust
================================================================================
coef std err t P>|t| [0.025 0.975]
--------------------------------------------------------------------------------
const 0.2501 0.098 2.561 0.011 0.057 0.443
petal_length 0.2304 0.034 6.691 0.000 0.162 0.298
setosa -0.3410 0.051 -6.655 0.000 -0.442 -0.240
versicolor 0.0944 0.054 1.751 0.082 -0.012 0.201
virginica 0.4967 0.096 5.150 0.000 0.306 0.687
==============================================================================
Omnibus: 6.210 Durbin-Watson: 1.736
Prob(Omnibus): 0.045 Jarque-Bera (JB): 9.578
Skew: -0.110 Prob(JB): 0.00832
Kurtosis: 4.218 Cond. No. 1.69e+16
==============================================================================
Warnings:
[1] Standard Errors assume that the covariance matrix of the errors is correctly specified.
[2] The smallest eigenvalue is 9.68e-30. This might indicate that there are
strong multicollinearity problems or that the design matrix is singular.
Avec cette version, on s’améliore en termes de mais la
précision de notre estimateur est plus faible…
Pour aller plus loin, de nombreux exemples sont disponibles là :