Régression logistique par morceaux, arbres de décision#

Ce qui suit explore une façon fantaisiste de construire des régressions logistiques à mi-chemin entre les arbres de décisions et les réseaux de neurones. Dans un premier temps, on s’intéresse uniquement à une classification binaire.

Parallèle entre un neurone et une régression logistique #

Les paragraphes Classification et La classification présente le problème de la classification qui consiste à trouver une fonction f qui maximise la vraisemblance du nuage de points $(X_i, y_i)_i$ où $X_i \in \R^d$ et $y_i \in \acc{0, 1}$ .

$\ln L(\Theta, X, y) = \sum_{i=1}^n y_i \ln f(\Theta, X_i) + (1-y_i) \ln (1-f(\Theta, X_i))$

Dans le cas de la régression logistique, la fonction f est définie comme suit :

$f(\Theta, X_i) = \frac{1}{1 + e^{-\sum_{k=1}^d \theta_k x_{ik}}}$

Cela ressemble beaucoup à la définition d’un neurone où la fonction d’activation $f(x) = \frac{1}{1 + e^{-x}}$ est une fonction sigmoïde.

Principe d’un arbre de décision #

Un arbre de décision se construit peu à peu en répétant toujours la même optimisation sur des sous-ensemble de plus en plus petit. Il faut d’abord un critère qui permette d’évaluer la pertinence de la division effectuée par un noeud de l’arbre. Pour un ensemble $(X_i, y_i)_{1 \infegal i \infegal n}$ , on peut estimer la probabilité $p(y_1, ..., y_n) = p(Y) = \frac{1}{n}\sum{i=1}^n y_i$ . Le critère de Gini G qui évalue la pertinence d’une classification est défini par $G(Y) = p(Y) (1 - p(Y))$ . Un autre critère est le gain d’information ou entropie H : $H(Y) = - p(Y) \ln p(Y) - (1-p(Y)) \ln (1 - p(Y))$ .

On note $Y_S$ l’ensemble des $\acc{y_i | i \in S}$ où S est un sous-ensemble. $S^C$ est noté le complémentaire.

Pour le premier noeud de l’arbre de décision, on calcule pour toutes les variables et toutes les observations la diminution du critère choisi :

$\begin{array}{rcl} S_{ik} &=& \acc{ m | x_{mk} \infegal x_{ik}} \\ \Delta_{ik} &=& H(Y) - ( H(Y_{S_{ik}}) + H(Y_{S_{ik}^C} ) \end{array}$

On choisit alors la variable k et le seuil $x_{ik}$ qui maximise le gain. Dans le cas d’une régression logistique, la vraisemblance correspond à :

$\ln L(\Theta, X, y) = \sum_{i=1}^n y_i \ln f(\Theta, X_i) + (1-y_i) \ln (1-f(\Theta, X_i))$

Si on suppose que la fonction f retourne une constante c, cette expression devient :

$\ln L(\Theta, X, y) = \sum_{i=1}^n y_i \ln c + (1-y_i) \ln (1-c) = p(Y) \ln c + (1-p(Y)) \ln (1-c)$

Or cette expression admet un maximum pour $c=p(Y)$ puisque la dérivée s’annule de façon évidente pour cette valeur :

$\frac{\partial \ln L(\Theta, X, y)}{\partial c} = \frac{p(Y)}{c} - \frac{1-p(Y)}{1-c}$

On remarque que l’optimisation d’un noeud d’un arbre de décision correspond à l’optimisation de la vraisemblance par une fonction constante. Une régression logistique calculée sur une seule variable est en quelque sorte une généralisation de ce modèle. On apprend un arbre de décision qu’on exporte au format dot.

<<<

from sklearn.datasets import load_iris
from sklearn.tree import DecisionTreeClassifier, export_graphviz
ds = load_iris()
X, y = ds.data, ds.target
y = y % 2
dt = DecisionTreeClassifier(max_depth=3, criterion='entropy')
dt.fit(X, y)
print(dt)
# export_graphviz(dt)

>>>

    DecisionTreeClassifier(criterion='entropy', max_depth=3)

Ce qui donne :

Construction d’un pseudo arbre #

Et si on remplaçait chaque noeud par une régression logistique appris sur les exemples passant par ce noeud… Plutôt que de prendre une décision basée sur une variable donnée et de retourner une probabilité constante, on estime une régression logistique et on retourne la probabilité retournée par la régression.

S’il n’y a théoriquement aucun obstacle, en pratique, certains cas posent quelques problèmes comme le montre l’exemple Arbre d’indécision et repris ci-dessous. La fonction criteria calcule les différents gains selon les points de coupure.

import matplotlib.pyplot as plt
from mlstatpy.ml.logreg import criteria, random_set_1d, plot_ds

X1, y1 = random_set_1d(1000, 2)
X2, y2 = random_set_1d(1000, 3)
X3, y3 = random_set_1d(1000, 4)
df1 = criteria(X1, y1)
df2 = criteria(X2, y2)
df3 = criteria(X3, y3)

fig, ax = plt.subplots(1, 3, figsize=(14, 5), sharey=True)
plot_ds(X1, y1, ax=ax[0], title="easy")
plot_ds(X2, y2, ax=ax[1], title="difficult")
plot_ds(X3, y3, ax=ax[2], title="more difficult")
df1.plot(x='X', y=['Gini', 'Gain', 'p1', 'p2'], ax=ax[0], lw=5.)
df2.plot(x='X', y=['Gini', 'Gain', 'p1', 'p2'], ax=ax[1], lw=5.)
df3.plot(x='X', y=['Gini', 'Gain', 'p1', 'p2'], ax=ax[2], lw=5.)
plt.show()

(png, hires.png, pdf)

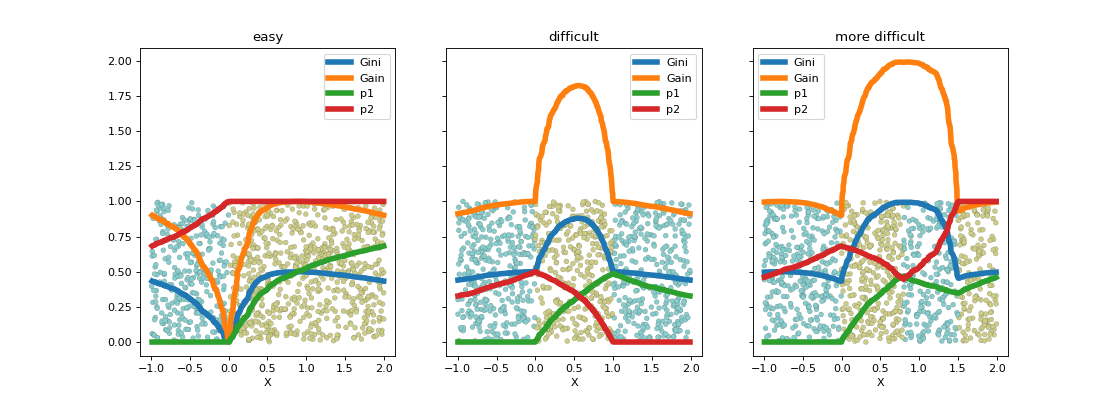
Le seuil de coupure est évident dans le premier cas et quasiment impossible à trouver de façon numérique dans le second avec les algorithmes tels qu’ils sont implémentés. Les arbres de décision contournent ce problème en imposant que le seuil de coupure laisse au moins quelques exemples de chaque côté ce que la régression logistique ne fait pas. On peut réflechir à d’autres critères. Le suivant explore la log-vraisemblance.

import matplotlib.pyplot as plt
from mlstatpy.ml.logreg import criteria2, random_set_1d, plot_ds

X1, y1 = random_set_1d(1000, 2)
X2, y2 = random_set_1d(1000, 3)
X3, y3 = random_set_1d(1000, 4)
df1 = criteria2(X1, y1)
df2 = criteria2(X2, y2)
df3 = criteria2(X3, y3)
print(df3)

fig, ax = plt.subplots(1, 3, figsize=(14, 5), sharey=True)
plot_ds(X1, y1, ax=ax[0], title="easy")
plot_ds(X2, y2, ax=ax[1], title="difficult")
plot_ds(X3, y3, ax=ax[2], title="more difficult")
df1.plot(x='X', y=['LL', 'LL-10', 'LL-100'], ax=ax[0], lw=5.)
df2.plot(x='X', y=['LL', 'LL-10', 'LL-100'], ax=ax[1], lw=5.)
df3.plot(x='X', y=['LL', 'LL-10', 'LL-100'], ax=ax[2], lw=5.)
plt.show()

(png, hires.png, pdf)

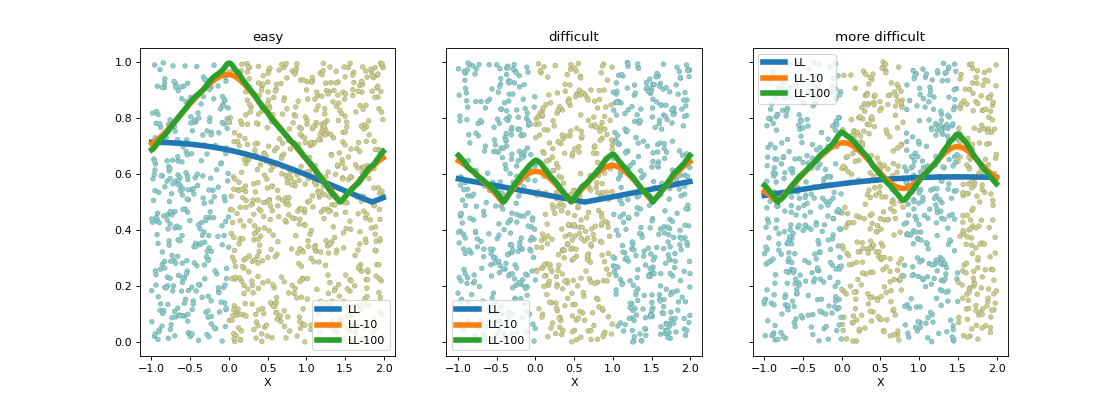
La log-vraisemblance dans ce problème à une dimension est assez simple à écrire. Pour avoir une expression qui ne change pas en invertissant les classes, on considère le maxiimum des vraisemblance en considérant deux classifieurs opposés. Le graphe précédent fait varier $x_0$ avec différents $\theta$ .

$LL(x_0, \theta) = \max \left\{ \begin{array}{ll} \frac{1}{1 + \exp{\left(\frac{x-x_0}{\theta}\right)}} \\ \frac{1}{1 + \exp{\left(-\frac{x-x_0}{\theta}\right)}} \end{array}\right.$

Aparté mathématique #

La log-vraisemblance d’une régression logistique pour un jeu de données $(X_i, y_i)$ s’exprime comme suit pour une régression logistique de paramètre $\beta$ .

$\begin{array}{rcl} L(\beta, X, y) &=& \sum_{i=1}^n y_i \ln f(\beta, X_i) + (1-y_i) \ln (1-f(\beta, X_i)) \\ \text{avec } f(\beta, X_i) &=& \frac{1}{1 + \exp(- (\beta_0 + \sum_{k=1}^d x_{ik} \beta_k))} \end{array}$

On remarque que :

$\begin{array}{rcl} f(x) &=& \frac{1}{1 + e^{-x}} \\ \Rightarrow f(-x) &=& \frac{1}{1 + e^{x}} = \frac{e^{-x}}{1 + e^{-x}} \\ \Rightarrow f(x) + f(-x) &=& \frac{1}{1 + e^{-x}} + \frac{e^{-x}}{1 + e^{-x}} = 1 \end{array}$

Cela explique pour on utilise souvent cette fonction pour transformer une distance en probabilité pour un classifieur binaire. L’apprentissage d’un arbre de décision sklearn.tree.DecisionTreeClassifier propose le paramètre min_samples_leaf. On se propose dans le cadre de la régression logistique de chercher le paramètre $\beta_0$ qui permet de vérifier la contrainte fixée par min_samples_leaf. Cela revient à trounver un classifieur linéaire parallèle au premier qui vérifie les contraintes.

Approche EM et régression logistique #

L’article [Scott2013] explicite un algorithme d’apprentissage EM pour une régression logistique.

Il faudrait adapter cet agorithme pour apprendre deux régressions logistiques dont la combinaison sur deux parties disjointes serait meilleure qu’une seule régression logistique sur la réunion des deux parties. Cet algorithme devrait trouver à la fois les modèles et la séparation entre les deux parties.

A faire(idée): Arbre de régressions logistiques et EM

Chaque noeud du graphe serait modélisé comme étant la réunion de trois régressions logistiques, une pour diviser l’espace en deux, deux autres apprenant à classifier sur chacune des parties.

issue

Lien vers les réseaux de neurones #

En remplaçant chaque noeud par une régression logistique, l’arbre de décision deviendrait un réseau de neurones, avec une structure particulière certes mais un réseau de neurones tout de même. Chaque noeud du graphe serait transformé en un neurone avec une régression logistique impliquant toutes les variables. Il ne resterait plus qu’à continuer l’apprentissage avec des algorithmes à base de gradient stochastique. Cela reviendrait à changer l’initialisation du réseau de neurones. On considère le petit arbre décision suivant, trois features, trois noeuds, deux classes.

On souhaite le transformer en réseau de neurones avec une structure qui serait celle qui suit. On note tout d’abord la fonction sigmoïde $f(x, s, h)=\frac{1}{1 + e^{-h(x - s)}}$ . Elle vaut 1/2 lorsque x vaut s, vaut 1 lorsque x est très grand, et 0 lorsque x est très petit. C’est équivalent à la fonction $f(x, s, h)=g(X, S, v_0, h)\frac{1}{1 + e^{h(<X,V> + v_0)}}$ où $X=(x_1, x_2, x_3)$ , $V=(-1, 0, 0)$ et $v_0=s$ .

Le problème avec la structure proposée est que chaque noeud final retourne toujours une classe alors que dans un arbre de décision, seule une feuille répond. Un noeud final fait la somme de toutes les feuilles, deux dans cet exemple. L’implémentation de scikit-learn n’est pas la plus facile à manipuler dans le sens où chaque couche ne peut prendre comme entrée que les sorties de la précédente et la fonction d’activation est la même pour tous les neurones. On ne peut pas non plus geler certains coefficients lors de l’apprentissage. C’est à ce moment-là qu’on se demande si ça vaut le coup de se lancer dans une implémentation à la rigueur jolie mais sans doute pas porteuse d’une innovation majeure. Et ce n’est pas la première fois que quelqu’un se lance dans la conversion d’un arbre en réseaux de neurones.

J’ai quand même essayé avec le notebook Un arbre de décision en réseaux de neurones et les classes NeuralTreeNode, NeuralTreeNet. Si l’idée de départ est séduisante, elle requiert une contrainte supplémentaire qui est de créer un réseau de neurones qui ne soit pas un minimum local de la fonction d’erreur auquel cas un apprentissage avec un algorithme à base de gradient ne pourra pas améliorer les performances du réseau de neurones.

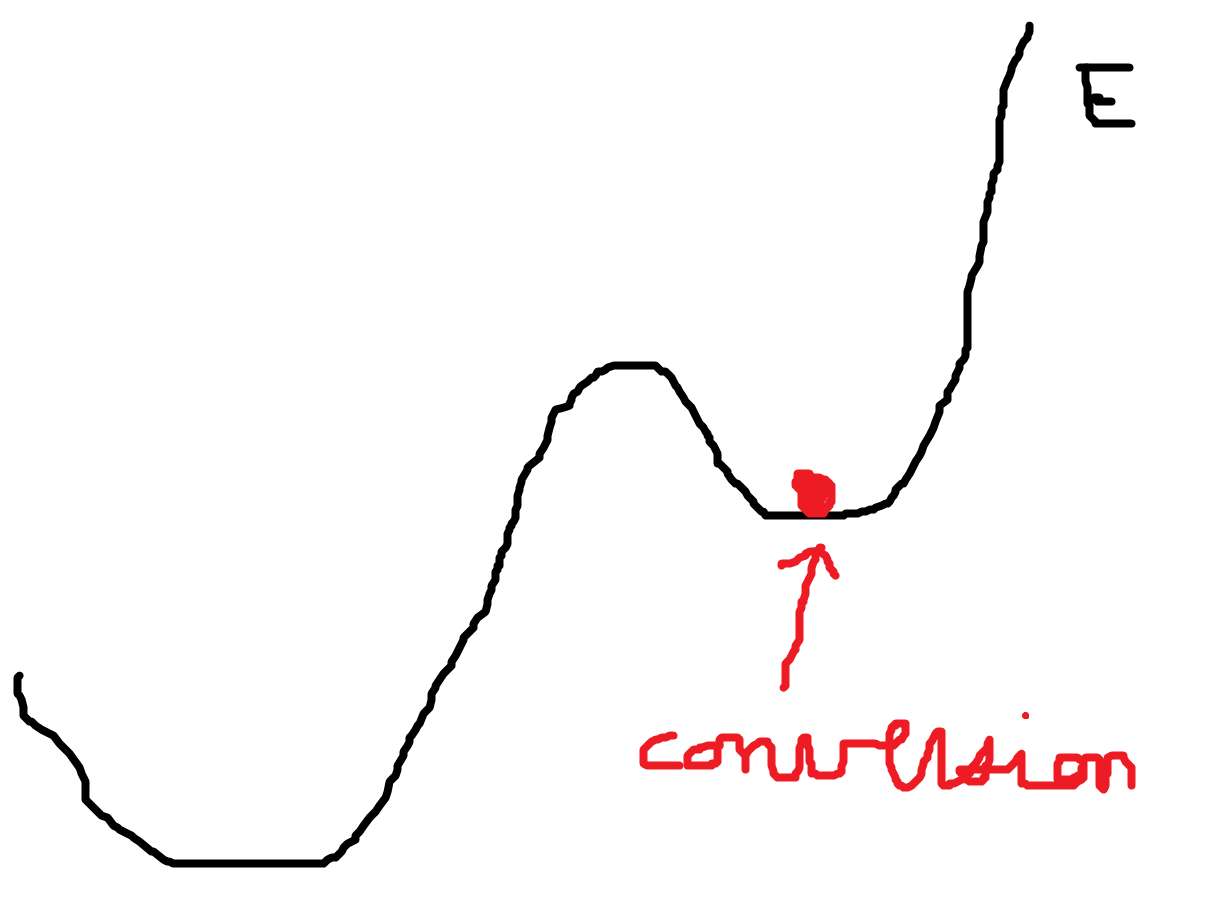
La structure proposée n’est cependant pas la meilleure et elle pourrait être simplifiée. D’autres projets s’appuie des librairies existantes :

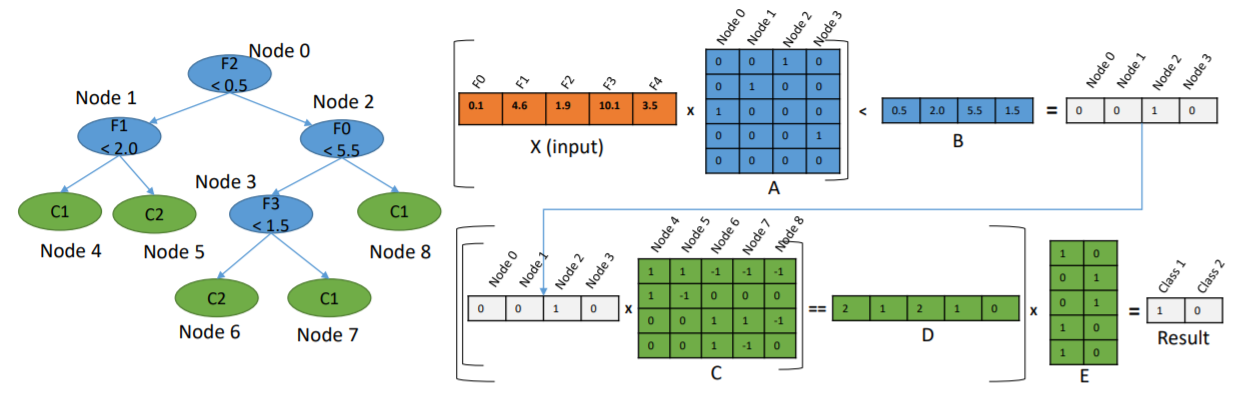
Ce dernier package convertit un réseau de neurones en autant de couches que la profondeur de l’arbre. L’image qui suit est tiré de l’article [Nakandalam2020] et qui résume leur idée.

Plan orthogonal #

Dans un espace à plusieurs dimensions, la régression logistique divise l’espace à l’aide d’un hyperplan. La fonction de décision reste similaire puisque la probabilité de classification dépend de la distance à cet hyperplan. On suppose qu’il existe une régression logistique binaire apprise sur un nuage de points $(X_i, y_i)$ . La probabilité de bonne classification est définie par :

$f(\Theta, X_i) = \frac{1}{1 + e^{-\theta_0 + \sum_{k=1}^d \theta_k x_{ik}}}$

Le vecteur $\Theta$ définit un hyperplan. On choisit un vecteur $\Theta'$ de telle sorte que $<\Theta,\Theta'> = 0$ . Les deux vecteurs sont orthogonaux. On définit maintenant deux autres vecteurs $\Theta_1, \Theta_2$ pour deux autres régressions logistiques. Pour classer un point $X$ , on procède comme suit :

si $<\Theta',X> < 0$ , on classe le point en appliquant la régression logistique définie par $Theta_1$ ,
si $<\Theta',X> \leqslant 0$ , on classe le point en appliquant la régression logistique définie par $Theta_2$ .

De manière évidente, les performances en classification sont les mêmes que la première régression logistique. On peut ensuite réestimer les vecteurs $\Theta_1, \Theta_2$ pour maximiser la vraisemblance sur chacune des parties. Il ne reste plus qu’à montrer que la vraisemblance globale sera supérieur à celle obtenue par la première régression logistique.

A faire(idée): Arbre de régressions logistiques en cascade orthogonale

Implémenter la l’algorithme suivant :

Apprendre une régression logistique
Choisir un hyperplan perpendiculaire en optimisation un critère Construction d’un pseudo arbre
Apprendre une régression logistique sur chacune des parties.
Continuer jusqu’à ce l’amélioration soit négligeable

issue

Interprétabilité #

Bibliographie #

[Scott2013] Expectation-maximization for logistic regression,: James G. Scott, Liang Sun
[Nakandalam2020] A Tensor-based Approach for One-size-fits-all ML Prediction Serving.: Supun Nakandalam, Karla Saur, Gyeong-In Yu, Konstantinos Karanasos, Carlo Curino, Markus Weimer, Matteo Interlandi. To appear at OSDI 2020.

Liens

Contenu

Information

Sujet précédent

Sujet suivant