Liens entre factorisation de matrices, ACP, k-means#

La factorisation de matrice non négative. Cette méthode est utilisée dans le cadre de la recommandation de produits à des utilisateurs. Lire également [Acara2011], [Gupta2010].

Factorisation de matrices et rang #

La factorisation d’une matrice est un problème d’optimisation qui consiste à trouver pour une matrice $M \in \mathcal{M}_{pq}$ à coefficients positifs ou nuls :

M = WH

Où $W$ et $H$ sont de rang $k$ et de dimension $W \in \mathcal{M}_{pk}$ et $H \in \mathcal{M}_{kq}$ . On s’intéresse ici au cas où les coefficients ne sont pas nécessairement positifs. Si $k < rang(M)$ , le produit $WH$ ne peut être égal à $M$ . Dans ce cas, on cherchera les matrices qui minimise :

Problème P1 : Factorisation de matrices positifs

Soit $M \in \mathcal{M}_{pq}$ , on cherche les matrices à coefficients positifs $W \in \mathcal{M}_{pk}$ et $H \in \mathcal{M}_{kq}$ qui sont solution du problème d’optimisation :

$\min_{W,H}\acc{\norme{M-WH}^2} = \min_{W,H} \sum_{ij} (m_{ij} - \sum_k w_{ik} h_{kj})^2$

Quelques cas simples #

Le notebook Valeurs manquantes et factorisation de matrices montre la décroissante de l’erreur en fonction du rang et l’impact de la corrélation sur cette même erreur. Le dernier paragraphe montre qu’il n’existe pas de solution unique à un problème donné. L’exemple suivant s’intéresse à une matrice 3x3. Les trois points forment un triangle dans un plan.

import matplotlib.pyplot as plt
from mpl_toolkits.mplot3d import Axes3D
from numpy import identity, array

M = identity(3)
W = array([[0.5, 0.5, 0], [0, 0, 1]]).T
H = array([[1, 1, 0], [0.0, 0.0, 1.0]])
wh = W @ H

fig = plt.figure()
ax = fig.add_subplot(111, projection='3d')

ax.scatter(M[:,0], M[:,1], M[:,2], c='b', marker='o', s=600, alpha=0.5)
ax.scatter(wh[:,0], wh[:,1], wh[:,2], c='r', marker='^')
plt.show()

(png, hires.png, pdf)

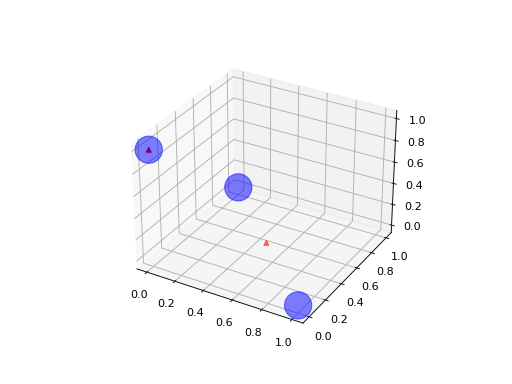
On peut voir la matrice $M$ comme un ensemble de $n=3$ points dans un espace vectoriel. La matrice $W$ est un ensemble de $k < n$ points dans le même espace. La matrice $WH$ , de rang $k$ est une approximation de cet ensemble dans le même espace, c’est aussi $n$ combinaisons linéaires de $k$ points de façon à former $n$ points les plus proches proches de $n$ points de la matrice $M$ .

Intuition géométrique #

L’exemple précédente suggère une interprétation géométrique d’une factorisation de matrice. Sans valeur manquante, ce problème est équivalent à une Analyse en Composantes Principales (ACP) (voir aussi [Boutsidis2008] (décomposition en valeurs singulières comme algorithme d’initialisation). Nous allons le montrer grâce à quelques lemmes et théorèmes.

Lemme L1 : Rang k

On note $M=(m_{ij})$ , $W^k=(w^k_{il})$ , $H^k=(h^k_{lj})$ avec $1 \infegal i \infegal p$ , $1 \infegal j \infegal q$ , et $1 \infegal l \infegal k$ avec $k < \min(p,q)$ . On suppose que les matrices sont solution du problème d’optimisation $\min_{W,H} \norm{ M - WH }^2$ . On suppose que $rang(M) \supegal k$ . Alors les les matrices $W^k$ et $H^k$ sont de rang $k$ .

On procède par récurrence. Ce lemme est nécessairement vrai pour $k=1$ car la matrice $M$ n’est pas nulle. De manière évidente, $\norm{ M - W^{k-1}H^{k-1} }^2 \supegal \norm{ M - W^kH^k }^2$ . Comme $rang(M) \supegal k$ , il existe un vecteur colonne $V$ de la matrice $M$ qui ne fait pas partie de l’espace vectoriel engendré par les $k-1$ vecteurs de la matrice $W^{k-1}$ . On construit la matrice $Y^k= [W^{k-1}, V]$ . Par construction, $rang(Y) = k$ . De même, on construit $G^k$ à partir de $H^{k-1}$ en remplaçant la dernière colonne et en ajoutant une ligne :

$G^k=\cro{\begin{array}{cc} H^{k-1}[1..p-1] & 0 \\ 0 & 1 \end{array}}$

Par construction, le dernier vecteur est de la matrice produit est identique à celui de la matrice $M$ .

$\norme{M - Y^{k-1}G^{k-1}}^2 = \norme{M - W^{k-1}H^{k-1}}^2 - \sum_i (m_{iq} - w^{k-1}_{ik} h^{k-1}_{kq})^2$

Nous avons fabriqué une matrice de rang k qui fait décroître l’erreur du problème d’optimisation. On procède par l’absurde pour dire que si $rang(W) = k-1$ , on peut construire une matrice de rang k qui fait décroître l’erreur ce qui est impossible. Le lemme est donc vrai.

Ce lemme fait également apparaître la construction de q points dans un espace vectoriel engendré par les k vecteurs colonnes de la matrice $W_k$ . Il est donc possible de choisir n’importe quel base $W'_{k}$ de cet espace et d’exprimer les q points de $W_kH_k$ avec cette nouvelle base. Cela signifie qu’on peut écrire la matrice $W_k$ dans une base $B_k$ comme $W_k = B_k C_k$ et $W_k H_k = B_k C_k C_k^{-1} G_k$ .

Lemme L2 : Projection

On note $M=(m_{ij})$ , $W^k=(w^k_{il})$ , $H^k=(h^k_{lj})$ avec $1 \infegal i \infegal p$ , $1 \infegal j \infegal q$ , et $1 \infegal l \infegal k$ avec $k < \min(p,q)$ . On suppose que les matrices sont solution du problème d’optimisation $\min_{W,H} \norm{ M - WH }^2$ . On considère que la matrice $M$ est un ensemble de $q$ points dans dans un espace vectoriel de dimension $p$ . La matrice $WH$ représente des projections de ces points dans l’espace vectoriel engendré par les $k$ vecteurs colonnes de la matrice $W$ .

La figure suivante illustre ce lemme. $\norm{ M - WH }^2$ s’écrit comme la somme des distances entre q points :

$\norm{ M - WH }^2 = \sum_{j=1}^q \norme{M[j] - W_kH_k[j]}^2$

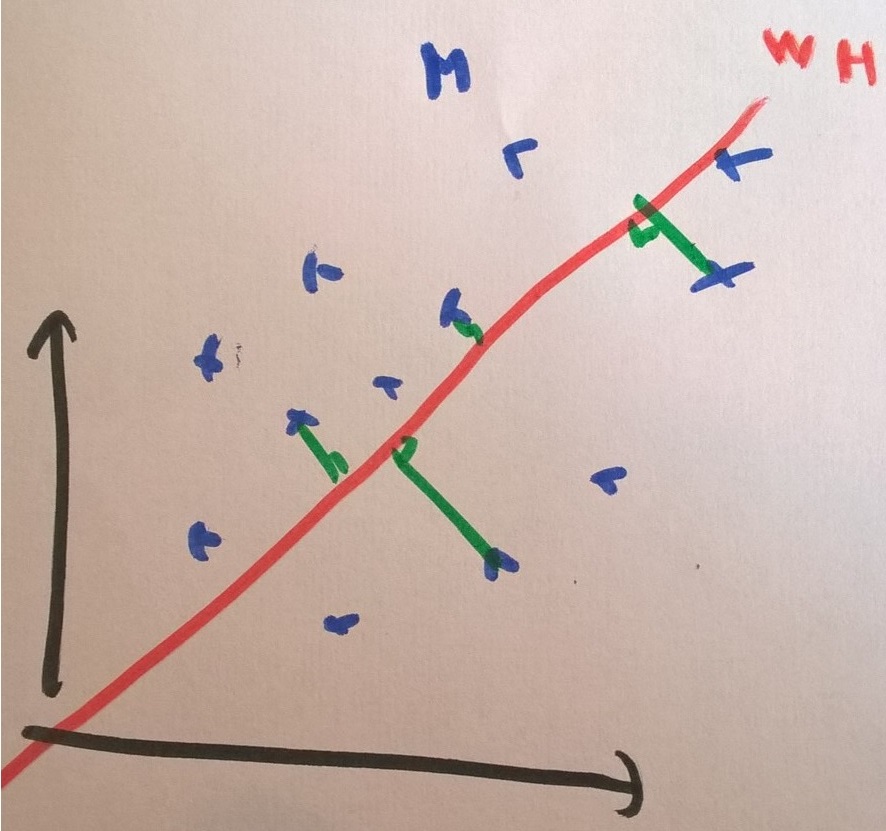
Or on sait que si $W_k$ est fixé, les q points de la matrice $W_kH_k$ évolue sur un hyperplan de dimension $k$ . Le point de ce plan le plus du vecteur $M[j]$ est sa projection sur ce plan.

Théorème T1 : La factorisation de matrice est équivalente à une analyse en composantes principales

On note $M=(m_{ij})$ , $W^k=(w^k_{il})$ , $H^k=(h^k_{lj})$ avec $1 \infegal i \infegal p$ , $1 \infegal j \infegal q$ , et $1 \infegal l \infegal k$ avec $k < \min(p,q)$ . On suppose que les matrices sont solution du problème d’optimisation $\min_{W,H} \norm{ M - WH }^2$ . On considère que la matrice $M$ est un ensemble de $q$ points dans dans un espace vectoriel de dimension $p$ . On suppose $p < q$ . La matrice $W_k$ définit un hyperplan identique à celui défini par les $k$ vecteurs propres associés aux $k$ plus grande valeurs propres de la matrice $MM'$ où $M'$ est la transposée de $M$ .

Une analyse en composante principale consiste à trouver l’hyperplan qui maximise l’inertie de la projection d’un nuage sur ce plan. Le théorème résolution de l’ACP a montré que :

(1)# $\begin{eqnarray*} S = \underset{ \begin{subarray}{c} W \in M_{p,d}\pa{\R} \\ W'W = I_d \end{subarray} } { \arg \max } \; \cro { \sum_{i=1}^{N} \norm{W'X_i}^2 } &=& \underset{ W \in M_{p,d}\pa{\R} } { \arg \min } \; \cro { \sum_{i=1}^{N} \norm{WW'X_i - X_i}^2 } \end{eqnarray*}$

Dans notre cas, chaque ligne de la matrice $M$ est un vecteur $X_i$ . La matrice $W_k$ est identique à celle cherchée lors du problème de factorisation de matrices. Les colonnes de la matrice $H_k$ sont égales à $W'X_i$ . Il reste à montrer que le minimum trouvé dans les deux problèmes est le même. Le notebook Factorisation et matrice et ACP montre que cela fonctionne sur un exemple. La démonstration du théorème montre également que $W'W = I_d$ et dans ce cas précis, $WW'X_i$ représente les coordonnées de la projection du point $X_i$ sur le plan défini par les vecteurs $W$ . C’est aussi ce que montre second lemmme. S’il s’agit du même plan, cela signifie que les deux formulations, ACP et factorisation de matrices, aboutissent au même minimum. Comme l’algorithme de l’ACP détermine le meilleur plan projecteur, nécessairement, il correspond à celui trouvé par la factorisation de matrice.

k-means #

On peut construire deux matrices $W$ et $H$ à partir des résultats d’un k-means. Celui-ci détermine $k$ centres auxquels on effecte les points du nuage de départ. Dans ce cas-ci, la matrice $W$ est constituée des coordonnées de ces centres. On note $C_l$ le cluster $l$ , la matrice $H^k=(h^k_{lj})$ est définie comme suit :

$h^k_{lj} = \indicatrice{X_j \in C_l}$

Les coefficients sont soit 0 ou 1. On peut alors essayer de forcer la factorisation de matrice vers une matrice $H$ avec pas de un 1 sur chaque colonne et des zéros partout ailleurs. Le résultat sera assez proche d’un clustering.

Quelques résultats #

Le notebook Factorisation et matrice et ACP illustre le lien entre ACP et factorisation de matrice en deux dimensions.

Prolongements #

Tous les résultats montrés ici ne sont valables que si la norme $L_2$ est utilisée. Cela permet de mieux comprendre les références proposées dans la documentation de Non-negative matrix factorization (NMF or NNMF). Si l’ACP et la factorisation de matrices sont équivalentes, les algorithmes pour trouver le minimum diffèrent et sont plus ou moins appropriés dans certaines configurations. Lire [Gilles2014].

Factorisation non-négative #

Le problème le plus souvent évoqué est celui de la factorisation non-négative : NMF. Ce problème est une optimisation avec contrainte : les coefficients doivent tous être positifs ou nuls. Il n’est bien sûr plus équivalent à une ACP. En revanche, la factorisation de matrice est un problème équivalent à celui résolu par la Décomposition en Valeur Singulière (SVD) qui cherche à décomposer une matrice $M=U\Sigma V^*$ . La matrice $\Sigma$ est une matrice diagonale et la matrice initiale M n’est pas nécessairement carrée contrairement au cas d’une ACP mais SVD et ACP sont très similaires.

Prédiction #

Prédire revient à supposer que la matrice $M$ est composée de vecteurs lignes $X_1, ..., X_q$ . La matrice $H$ reste inchangée et la prédiction revient à déterminer les coordonnées de la projection d’un nouveau point $X_{q+1}$ dans le plan défini par les vecteurs de la matrice $H$ . Pour de nouvelles observations $M_2=X_{q+1}$ , la fonction transform de la classe sklearn.decomposition.NMF réestime une matrice $W_2$ qui projette les vecteurs lignes de $M_2$ sur les vecteurs de H en conservant des coefficients de projection positifs.

Problème P2 : Prédiction

Soit $M \in \mathcal{M}_{pq}$ et $H \in \mathcal{M}_{kq}$ , on cherche les matrices à coefficients positifs $W \in \mathcal{M}_{pk}$ qui sont solution du problème d’optimisation :

$\min_{W}\acc{\norme{M-WH}^2} = \min_{W,H} \sum_{ij} (m_{ij} - \sum_k w_{ik} h_{kj})^2$

Les recommandations s’obtiennent en multipliant $W_2$ par $X_{q+1}$ . Ce produit peut être approchée en relâchant la contrainte des poids positifs pour la matrice W. C’est la piste proposée par le modèle ApproximateNMFPredictor qui utilise une transformation SVD pour projeter sur l’espace vectoriel formé par les vecteurs de H.

Norme #

L’ACP avec une norme $L_1$ revient à trouver le plan qui minimise la somme des distances à la projection et non la somme des distances au carrés. Cela réduit l’impact des points aberrants mais le problème n’est plus équivalent à la factorisation de matrices avec une norme $L_1$ .

Sparsité #

Une ACP suppose que le calcul de valeurs propres d’une matrice et c’est fastidieux lorsque la dimension du problème est très grande. On lui préfère alors un algorithme tel que Sparse PCA. La factorisation de matrice est plus efficace qu’une ACP sur les problèmes sparses et de grande dimension. Lire Non-negative Matrix Factorization with Sparseness Constraints.

Valeurs manquantes #

Contourner le problème des valeurs manquantes veut souvent dire, soit supprimer les enregistrements contenant des valeurs manquantes, soit choisir un modèle capable de faire avec ou soit trouver un moyen de les remplacer. On peut gérer plus facilement le problème des valeurs manquantes avec une factorisation de matrices. On peut également se server de la méthode pour calculer une ACP avec des valeurs manquantes.

Interprétation #

La factorisation de matrice peut être utilisée comme outil de segmentation et d’interprétation pour des images, des vidéos. Lire A tutorial on Non-Negative Matrix Factorisation with Applications to Audiovisual Content Analysis.

Gesture recognition using a NMF-based representation of motion-traces extracted from depth silhouettes

NTF #

Le problème de Non-Negative Matrix Factorisation (NMF) est un cas particulier de Non-Negative Tensor Factorisation (NTF). Lire aussi PARAFAC. Tutorial and applications.

Bibliographie #

[Acara2011]

Scalable tensorfactorizations for incomplete data, Evrim Acara Daniel, M.Dunlavyc, Tamara G.Koldab. Morten Mørupd, Chemometrics and Intelligent Laboratory Systems, Volume 106, Issue 1, 15 March 2011, Pages 41-56, or ArXiv 1005.2197

[Boutsidis2008]

SVD-based initialization: A head start for nonnegative matrix factorization. Christos Boutsidis and Efstratios Gallopoulos Pattern Recognition, 41(4): 1350-1362, 2008.

[Gilles2014]

The Why and How of Nonnegative Matrix Factorization, Nicolas Gillis, ArXiv 1401.5226

[Gupta2010]

Additive Non-negative Matrix Factorization for Missing Data, Mithun Das Gupta, ArXiv 1007.0380

Liens

Contenu

Information

Sujet précédent

Sujet suivant