Analyse en composantes principales (ACP) et Auto Encoders#
Cet algorithme est proposé dans [Song1997]. Autrefois réseau diabolo, le terme auto-encoder est plus utilisé depuis l’avénement du deep learning. Il s’agit de compresser avec perte un ensemble de points. L”ACP est une forme de compression linéaire puisqu’on cherche à préserver l’information en projetant un nuage de points de façon à maximiser l’inertie du nuage. Les auto-encoders fonctionnent sur le même principe avec des modèles non linéaires.
subsection{Principe}
L’algorithme implémentant l’analyse en composantes principales
est basé sur un réseau linéaire dit « diabolo », ce réseau
possède une couche d’entrées à entrées, une couche cachée et une couche
de sortie à
sorties. L’objectif est
d’apprendre la fonction identité sur l’espace
.
Ce ne sont plus les sorties qui nous intéressent mais la couche
cachée intermédiaire qui effectue une compression ou projection
des vecteurs d’entrées puisque les entrées et les
sorties du réseau auront pour but d’être identiques.
Figure F1 : Principe de la compression par un réseau diabolo
La figure suivante illustre un exemple de compression de vecteur de
dans
.
Figure F2 : Réseau diabolo : réduction d’une dimension
Ce réseau possède 3 entrées et 3 sorties
Minimiser l’erreur
revient à compresser un vecteur de dimension 3 en un vecteur de dimension 2.
Les coefficients de la
première couche du réseau de neurones permettent de compresser les données.
Les coefficients de la seconde couche permettent de les décompresser.
La compression et décompression ne sont pas inverses l’une de l’autre, à moins que l’erreur (1) soit nulle. La décompression s’effectue donc avec des pertes d’information. L’enjeu de l’ACP est de trouver un bon compromis entre le nombre de coefficients et la perte d’information tôlérée. Dans le cas de l’ACP, la compression est « linéaire », c’est une projection.
Problème de l’analyse en composantes principales#
L’analyse en composantes principales ou ACP est définie de la manière suivante :
Problème P1 : analyse en composantes principales (ACP)
Soit avec
.
Soit
,
où les vecteurs
sont les colonnes de
et
.
On suppose également que les
forment une base othonormée.
Par conséquent :
est l’ensemble des
vecteurs
projetés sur le sous-espace vectoriel
engendré par les vecteurs
.
Réaliser une analyse en composantes principales, c’est trouver le
meilleur plan de projection pour les vecteurs
, celui qui maximise l’inertie de ce nuage de points,
c’est donc trouver
tel que :
(1)#
Le terme est l’inertie du nuage de points
projeté sur le sous-espace vectoriel défini par les
vecteurs colonnes de la matrice
.
Résolution d’une ACP avec un réseau de neurones diabolo#
Un théorème est nécessaire avant de construire le réseau de neurones menant à la résolution du problème de l”ACP afin de passer d’une optimisation sous contrainte à une optimisation sans contrainte.
Théorème T1 : résolution de l’ACP
Les notations utilisées sont celles du problème de l”ACP. Dans ce cas :
(2)#
De plus est l’espace vectoriel engendré par les
vecteurs propres de la matrice
associées aux
valeurs propres de plus grand module.
Démonstration
Partie 1
L’objectif de cette partie est de chercher la valeur de :
Soit , alors :
La matrice est symétrique, elle est donc diagonalisable
et il existe une matrice
telle qu :
(3)#
Soit les vecteurs propres de la matrice
associés aux valeurs propres
telles que
.
Pour mémoire,
, et on a :
D’où :
Donc :
(4)#
Partie 2
Soit ,
.
Chaque vecteur est écrit dans la base
définie en (3) :
Comme , les vecteurs
sont orthogonaux deux à deux et normés, ils vérifient donc :
De plus :
On en déduit que :
D’où :
Et :
Ceci permet d’affirmer que :
(5)#
Les équations (4) et (5) démontrent la seconde partie du théorème.
Partie 3
D’où :
(6)#
Partie 4
est une matrice symétrique, elle est donc diagonalisable :
On en déduit que :
D’où :
(7)#
Finalement, l’équation (7) permet de démontrer la première partie du théorème, à savoir (2) :
Calcul de valeurs propres et de vecteurs propres#
Le calcul des valeurs propres et des vecteurs propres d’une
matrice fait intervenir un réseau diabolo composé d’une
seule couche cachée et d’une couche de sortie avec des fonctions
de transfert linéaires. On note sous forme de matrice
les coefficients de la seconde couche
du réseau dont les biais sont nuls. On note
le nombre de
neurones sur la couche cachée, et
le nombre d’entrées.
Soit les entrées,
,
on obtient que :
.
Les poids de la seconde couche sont définis comme suit :
Par conséquent, le vecteur des sorties
du réseau ainsi construit est
.
On veut minimiser l’erreur pour
:
Il suffit d’apprendre le réseau de neurones pour obtenir :
D’après ce qui précède, l’espace engendré par les vecteurs
colonnes de est l’espace engendré par les
premiers vecteurs propres de la matrice
associés aux
premières valeurs propres classées par ordre décroissant de module.
On en déduit que est le vecteur propre de la matrice
associée à la valeur propre de plus grand module.
est l’espace engendré par les deux premiers vecteurs.
Grâce à une orthonormalisation de Schmidt.
On en déduit à partir de
et
,
les deux premiers vecteurs propres. Par récurrence,
on trouve l’ensemble des vecteurs propres de la matrice
.
Définition D1 : orthonormalisation de Schmidt
L’orthonormalisation de Shmidt :
Soit
une base de
On définit la famille
par :
On vérifie que le dénominateur n’est jamais nul.
car
Propriété P1 : base orthonormée
La famille
est une base orthonormée de
.
L’algorithme qui permet de déterminer les vecteurs propres de la matrice
définie par le théorème de l”ACP est le suivant :
Algorithme A1 : vecteurs propres
Les notations utilisées sont celles du théorème de l”ACP.
On note la matrice des
vecteurs propres de la matrice
associés aux
valeurs propres de plus grands module.
Analyse en Composantes Principales (ACP)#
L’analyse en composantes principales permet d’analyser
une liste d’individus décrits par des variables.
Comme exemple, il suffit de prendre les informations
extraites du recensement de la population française
qui permet de décrire chaque habitant par des
variables telles que la catégorie socio-professionnelle,
la salaire ou le niveau d’étude.
Soit un ensemble de
individus décrits par
variables :
L’ACP consiste à projeter ce nuage de point sur un plan qui conserve le maximum d’information. Par conséquent, il s’agit de résoudre le problème :
Ce problème a été résolu dans les paragraphes Problème de l’analyse en composantes principales et Calcul de valeurs propres et de vecteurs propres, il suffit d’appliquer l’algorithme vecteurs propres.
Soit avec
.
Soit
l’ensemble des vecteurs propres
normés de la matrice
associés aux valeurs propres
classées par ordre décroissant de modules.
On définit
.
On définit alors l’inertie
du nuage de points projeté sur
l’espace vectoriel défini par
.
On suppose que le nuage de points est centré, alors :
Comme est une base orthonormée de
,
on en déduit que :
De manière empirique, on observe fréquemment que la courbe
montre un point
d’inflexion (voir figure ci-dessous). Dans cet exemple, le point
d’inflexion correspond à
. En
analyse des données, on considère empiriquement que seuls les
quatres premières dimensions contiennent de l’information.
Figure F3 : Courbe d’inertie pour l’ACP
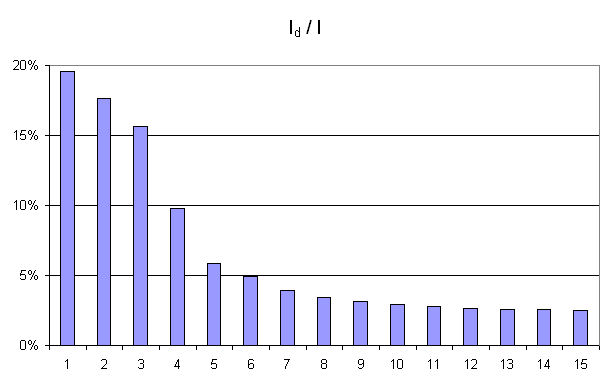
Courbe d’inertie : point d’inflexion pour ,
l’expérience montre que généralement, seules les
projections sur un ou plusieurs des quatre premiers vecteurs propres
reflètera l’information contenue par le nuage de points.