Régression

Un problème de régression consiste à construire une fonction qui prédit une quantité réelle Y en fonction de variables X. C’est une façon d’exprimer un lien entre deux quantités en fonction des observations (voir régression). La régression linéaire est le modèle le plus simple et consiste à supposer que la relation est linéaire.

Principe

On commence par générer un jeu de données artificiel.

from sklearn.tree import DecisionTreeRegressor
from sklearn.metrics import mean_squared_error
from sklearn.model_selection import train_test_split
from sklearn.linear_model import LinearRegression
import matplotlib.pyplot as plt
from sklearn.datasets import make_friedman1
X, Y = make_friedman1(n_samples=500, n_features=5)

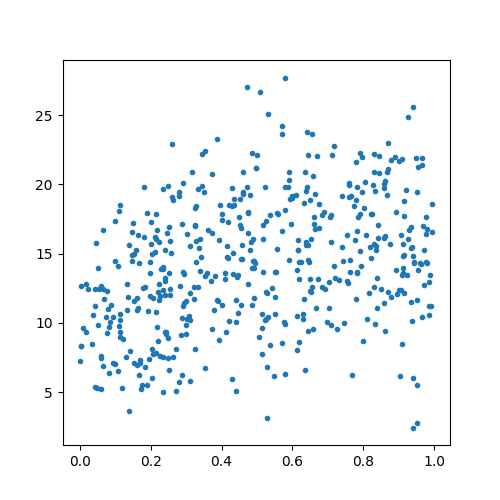
On représente ces données.

fig = plt.figure(figsize=(5, 5))
ax = plt.subplot()
ax.plot(X[:, 0], Y, '.')

[<matplotlib.lines.Line2D object at 0x7f5f3ae7f940>]

D’un point de vue géométrique, un problème de régression consiste à trouver la courbe qui s’approche au plus de tous les points. Le plus simple est de supposer que c’est une droite. Dans ce cas, on choisira un modèle de régression linéaire : LinearRegression.

reglin = LinearRegression()
reglin.fit(X, Y)

LinearRegression()

In a Jupyter environment, please rerun this cell to show the HTML representation or trust the notebook.
On GitHub, the HTML representation is unable to render, please try loading this page with nbviewer.org.

L’optimisation du modèle produit une droite dont les coefficients sont :

print(reglin.coef_, reglin.intercept_)

[ 5.93230458  6.3621584  -0.87201488  9.60041851  5.02910954] 1.342482246756484

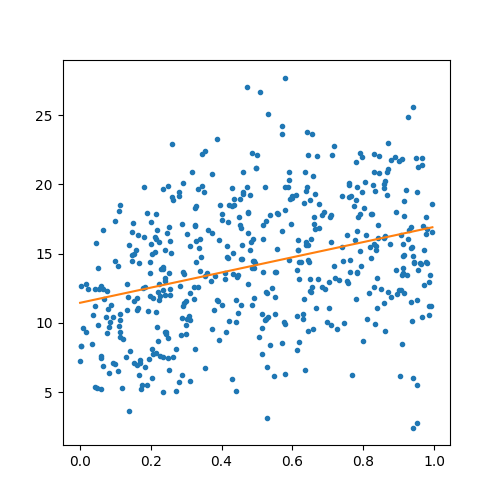
On reprend le premier graphe est on y ajoute la droite qui correspond à la régression linéaire uniquement sur la première dimension.

reglin = LinearRegression()
reglin.fit(X[:, :1], Y)

fig = plt.figure(figsize=(5, 5))
ax = plt.subplot()
x = list(sorted(X[:, :1]))
y = reglin.predict(x)
ax.plot(X[:, 0], Y, '.')
ax.plot(x, y)

[<matplotlib.lines.Line2D object at 0x7f5f3ec352b0>]

Evaluation

Le critère d’erreur le plus utilisé est l’erreur quadratique. Si est la valeur à prédire, et la valeur prédite, l’erreur est :

La plupart des problèmes sont multidimensionnelles et s’appuie sur de nombreuses variables mais bien souvent la valeur à prédire est réelle. On représente donc le graphique XY où l’axe des abscisses représente la valeur à prédire et l’axe des ordonnées la valeur prédite. On découpe d’abord en train/test.

X_train, X_test, y_train, y_test = train_test_split(X, Y)

On apprend un modèle.

reglin = LinearRegression()
reglin.fit(X_train, y_train)

LinearRegression()

In a Jupyter environment, please rerun this cell to show the HTML representation or trust the notebook.
On GitHub, the HTML representation is unable to render, please try loading this page with nbviewer.org.

On prédit.

pred = reglin.predict(X_test)

On calcule l’erreur.

err = mean_squared_error(y_test, pred)
print(err)

7.448159243320464

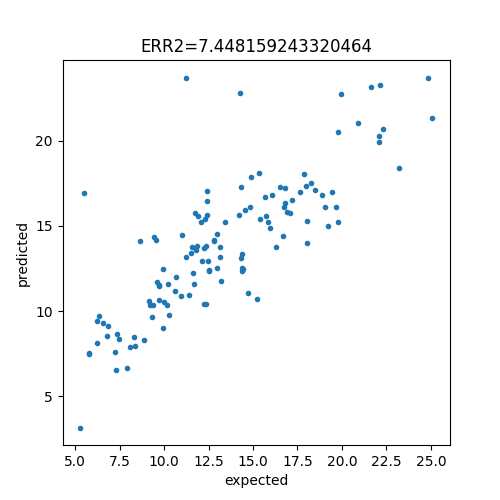
On dessine.

fig = plt.figure(figsize=(5, 5))
ax = plt.subplot()
ax.plot(y_test, pred, '.')
ax.set_xlabel("expected")
ax.set_ylabel("predicted")
ax.set_title(f"ERR2={err}")

Text(0.5, 1.0, 'ERR2=7.448159243320464')

Comparer deux modèles

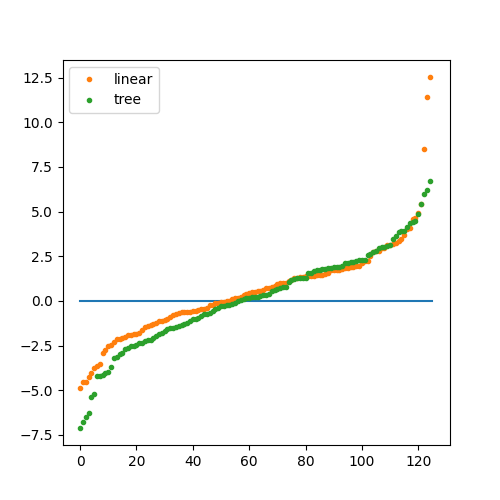
On peut bien évidemment les comparer numériquement. Graphiquement, les nuages de points s’entremêlent et deviennent peu visible. Pour y remédier, on trie les erreurs par ordre croissant.

regtree = DecisionTreeRegressor()
regtree.fit(X_train, y_train)
pred_tree = regtree.predict(X_test)

On dessine.

y1 = list(sorted(pred - y_test))
y2 = list(sorted(pred_tree - y_test))
fig = plt.figure(figsize=(5, 5))
ax = plt.subplot()
ax.plot([0, len(y1)], [0, 0], '-')
ax.plot(y1, '.', label="linear")
ax.plot(y2, '.', label="tree")
ax.legend()


plt.show()