Régression Ridge, Lasso et nouvel estimateur#
Links: notebook, html, PDF, python, slides, GitHub
Ce notebook présente la régression Ridge, Lasso, et l’API de scikit-learn. Il explique plus en détail pourquoi la régression Lasso contraint les coefficients de la régression à s’annuler.
from jyquickhelper import add_notebook_menu
add_notebook_menu()
%matplotlib inline
Un jeu de données pour un problème de régression#
from sklearn.datasets import load_diabetes
data = load_diabetes()
X, y = data.data, data.target / 10
/ 10 ou normaliser pour éviter les problèmes numériques lors que
l’optimisation.
from sklearn.model_selection import train_test_split
X_train, X_test, y_train, y_test = train_test_split(X, y)
On apprend la première régression linéaire.
from sklearn.linear_model import LinearRegression
lin = LinearRegression()
lin.fit(X_train, y_train)
lin.coef_
array([ -1.85601658, -26.87675858, 52.51732752, 32.38651524,
-64.19320341, 27.09717642, 8.31587784, 25.09987118,
65.75799437, 11.66015126])
from sklearn.metrics import r2_score
r2_score(y_test, lin.predict(X_test))
0.481884247676001
Régression Ridge#
La régression Ridge optimise le problème qui suit :
C’est une régression linéaire avec une contrainte quadratique sur les coefficients. C’est utile lorsque les variables sont très corrélées, ce qui fausse souvent la résolution numérique. La solution peut s’exprimer de façon exacte.
On voit qu’il est possible de choisir un pour lequel la
matrice
est inversible. C’est aussi utile
lorsqu’il y a beaucoup de variables car la probabilité d’avoir des
variables corrélées est grande. Il est possible de choisir un
suffisamment grand pour que la matrice $ (X’X +
:raw-latex:`alpha `I)^{-1}$ soit inversible et la solution unique.
from sklearn.linear_model import Ridge
rid = Ridge(10).fit(X_train, y_train)
r2_score(y_test, rid.predict(X_test))
0.08787659718647478
(r2_score(y_train, lin.predict(X_train)),
r2_score(y_train, rid.predict(X_train)))
(0.5131706866748321, 0.15127384319545023)
La contrainte introduite sur les coefficients augmente l’erreur sur la base d’apprentissage mais réduit la norme des coefficients.
import numpy
import matplotlib.pyplot as plt
r = numpy.abs(lin.coef_) / numpy.abs(rid.coef_)
fig, ax = plt.subplots(1, 1, figsize=(4, 4))
ax.plot(r)
ax.set_title("Ratio des coefficients\npour une régression Ridge");
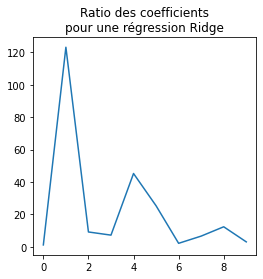
Un des coefficients est 10 fois plus grand et la norme des coefficients est plus petite.
numpy.linalg.norm(lin.coef_), numpy.linalg.norm(rid.coef_)
(120.61100965823518, 11.521828630313518)
De fait, il est préféreable de normaliser les variables avant d’appliquer la contrainte.
rid = Ridge(0.2).fit(X_train, y_train)
r2_score(y_test, rid.predict(X_test))
0.47199486845157335
numpy.linalg.norm(lin.coef_), numpy.linalg.norm(rid.coef_)
(120.61100965823518, 71.97787365561571)
Régression Lasso#
La régression Lasso optimise le problème qui suit :
C’est une régression linéaire avec une contrainte linéaire sur les coefficients. C’est utile lorsque les variables sont très corrélées, ce qui fausse souvent la résolution numérique. La solution ne s’exprime de façon exacte et la résolution utilise une méthode à base de gradient.
from sklearn.linear_model import Lasso
las = Lasso(5.).fit(X_train, y_train)
las.coef_
array([ 0., 0., 0., 0., 0., 0., -0., 0., 0., 0.])
On voit que beaucoup de coefficients sont nuls.
las.coef_ == 0
array([ True, True, True, True, True, True, True, True, True,
True])
sum(las.coef_ == 0)
10
Comme pour la régression Ridge, il est préférable de normaliser. On
étudie également le nombre de coefficients nuls en fonction de la valeur
.
from tqdm import tqdm
res = []
for alf in tqdm([0.00001, 0.0001, 0.005, 0.01, 0.015,
0.02, 0.025, 0.03, 0.04, 0.05, 0.06,
0.07, 0.08, 0.09, 0.1, 0.2, 0.3, 0.4]):
las = Lasso(alf).fit(X_train, y_train)
r2 = r2_score(y_test, las.predict(X_test))
res.append({'lambda': alf, 'r2': r2,
'nbnull': sum(las.coef_ == 0)})
from pandas import DataFrame
df = DataFrame(res)
df.head(5)
100%|██████████| 18/18 [00:00<00:00, 482.13it/s]
| lambda | r2 | nbnull | |
|---|---|---|---|
| 0 | 0.00001 | 0.481844 | 0 |
| 1 | 0.00010 | 0.481440 | 0 |
| 2 | 0.00500 | 0.487357 | 2 |
| 3 | 0.01000 | 0.488860 | 2 |
| 4 | 0.01500 | 0.488398 | 3 |
fig, ax = plt.subplots(1, 2, figsize=(8, 3))
ax[0].plot(df['lambda'], df['r2'], label='r2')
ax[1].plot(df['lambda'], df['nbnull'], label="nbnull")
ax[1].plot(df['lambda'], las.coef_.shape[0] - df['nbnull'], label="nbvar")
ax[0].set_xscale('log'); ax[1].set_xscale('log')
ax[0].set_xlabel("lambda"); ax[1].set_xlabel("lambda")
ax[0].legend(); ax[1].legend();
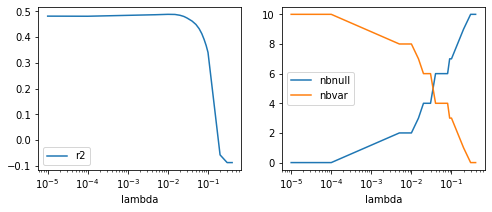
La régression Lasso annule les coefficients, voire tous les coefficients
si le paramètre est assez grand. Voyons cela pour une
régression avec une seule variable. On doit minimiser l’expression :
Trouver qui minimise l’expression nécessite de trouver
le paramètre
tel que
. On calcule la
dérivée
:
Et :
On voit que pour une grande valeur de ,
le paramètre
n’a pas de solution. Dans le premier cas, la
valeur est nécessairement négative alors que la solution ne fonctionne
que si
est positive. C’est la même situation
contradictoire dans l’autre cas. La seule option possible lorsque
est très grand, c’est
. On montre donc
que ce qu’on a observé ci-dessus est vrai pour une régression à une
dimension.
Application à la sélection d’arbre d’une forêt aléatoire#
Une forêt aléatoire est simplement une moyenne des prédictions d’arbres de régression.
Pourquoi ne pas utiliser une régression Lasso pour réduire le nombre
d’arbres et exprimer la forêt aléatoire avec des coefficients
estimés à l’aide d’une régression Lasso et choisis de
telle sorte que beaucoup soient nuls.
from sklearn.ensemble import RandomForestRegressor
rf = RandomForestRegressor(100).fit(X_train, y_train)
La prédiction d’un arbre s’obtient avec :
rf.estimators_[0].predict(X_test)
array([ 6.4, 34.1, 8.8, 8.5, 6.5, 9. , 11.5, 9.9, 5.1, 27.5, 5.9,
34.6, 12.3, 18.3, 5.1, 6.5, 27.7, 25.8, 9.4, 9.6, 16.3, 8.3,
27.7, 8.5, 6.4, 14. , 6.7, 17.4, 28.1, 14. , 8.5, 27.5, 18. ,
14.8, 7.2, 10.2, 16.8, 6.7, 18.1, 16.8, 9.4, 27.7, 6.8, 16.3,
28.1, 34.6, 18.1, 9.6, 10.2, 25.9, 18. , 5.9, 17.5, 16.4, 18. ,
9.6, 10.2, 11.1, 24.8, 17.4, 9.3, 5.1, 5.1, 5.9, 20.9, 9.5,
6.9, 11.5, 27.5, 10.2, 14. , 5.1, 11.8, 10.3, 7.1, 20. , 27.7,
10.2, 14.4, 9.1, 5.9, 11.4, 12.8, 14. , 16.1, 5.5, 8.8, 18.3,
5.1, 29.3, 12.8, 18.5, 18.1, 6.4, 17.2, 8.5, 9.3, 9.3, 31.1,
9.7, 34.6, 14.3, 15.1, 13.1, 19.9, 29.3, 19.6, 6.6, 14.3, 31.1,
19.6])
On construit une fonction qui concatène les prédictions des arbres.
def concatenate_prediction(X):
preds = []
for i in range(len(rf.estimators_)):
pred = rf.estimators_[i].predict(X)
preds.append(pred)
return numpy.vstack(preds).T
concatenate_prediction(X_test).shape
(111, 100)
Et on observe la performance en fonction du paramètre de
la régression Lasso.
X_train_rf = concatenate_prediction(X_train)
X_test_rf = concatenate_prediction(X_test)
res = []
for alf in tqdm([0.0001, 0.01, 0.1, 0.2, 0.5, 1.,
1.2, 1.5, 2., 4., 6., 8., 10., 12.,
14, 16, 18, 20]):
las = Lasso(alf, max_iter=40000).fit(X_train_rf, y_train)
r2 = r2_score(y_test, las.predict(X_test_rf))
r2_rf = r2_score(y_test, rf.predict(X_test))
res.append({'lambda': alf, 'r2': r2, 'r2_rf': r2_rf,
'nbnull': sum(las.coef_ == 0)})
100%|██████████| 18/18 [00:01<00:00, 17.32it/s]
df = DataFrame(res)
df.head(3)
| lambda | r2 | r2_rf | nbnull | |
|---|---|---|---|---|
| 0 | 0.0001 | 0.379155 | 0.447083 | 0 |
| 1 | 0.0100 | 0.379568 | 0.447083 | 2 |
| 2 | 0.1000 | 0.387457 | 0.447083 | 22 |
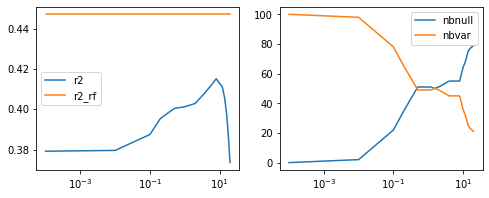
fig, ax = plt.subplots(1, 2, figsize=(8, 3))
ax[0].plot(df['lambda'], df['r2'], label='r2')
ax[0].plot(df['lambda'], df['r2_rf'], label='r2_rf')
ax[1].plot(df['lambda'], df['nbnull'], label="nbnull")
ax[1].plot(df['lambda'], las.coef_.shape[0] - df['nbnull'], label="nbvar")
ax[0].set_xscale('log'); ax[1].set_xscale('log')
ax[0].legend(); ax[1].legend();
Explication géométrique de la nullité des coefficients dans une régression Lasso#
On se place dans le cas d’un modèle très simple :
. Les coefficients
optimaux sont obtenus en minimisant l’erreur
. On
note
.
est l’erreur de régression,
est l’erreur de Lasso. Les
coefficients optimaux pour l’erreur
sont
. On représente
maintenant sur un graphe les courbes de niveaux de ces deux erreurs.
import math
def xyl1(t): return t, numpy.minimum(1 - t, t + 1)
def xyl2(t): return t, numpy.minimum(2.3 - t, t + 2.3)
def xyl3(t): return t, 0.4 - t
t = numpy.arange(1000) * 2 * math.pi / 1000
t2 = numpy.arange(500) / 500 - 0.2
fig, ax = plt.subplots(1, 1)
#ax.text(0.35, 2.7, "lambda1")
#ax.text(0.05, 2.5, "lambda2")
ax.plot([0.66], [1.66], "yo", label="a^*", ms=10)
ax.plot([0.0], [1.], "yo", ms=10)
ax.plot([0.0], [0.5], "yo", ms=10)
#ax.plot([0.0], [2.5], "yo")
ax.plot([0, 0], [0, 3], 'k--')
ax.plot([0, 2], [0, 0], 'k--')
ax.plot(numpy.cos(t) * 0.5 + 1, numpy.sin(t) * 0.5 + 2, "g", label="Er")
ax.plot(numpy.cos(t) * 2 ** 0.5 + 1, numpy.sin(t) * 2 ** 0.5 + 2, "g", lw=4)
ax.plot(numpy.cos(t) * 1.8 + 1, numpy.sin(t) * 1.8 + 2, "g", lw=6)
x, y = xyl1(t2); ax.plot(x, y, "r", label="El")
x, y = xyl2(t2); ax.plot(x, y, "r", lw=4)
x, y = xyl3(t2-0.5); ax.plot(x, y, "r--", lw=2)
ax.legend();
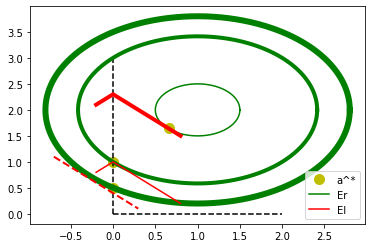
reste constante sur un cercle.
reste constante
sur une droite. Le point optimal solution de la régression Ridge est sur
la tangente entre le cercle et la droite. Lorsqu’on augmente
, il faut réduire l’erreur, donc passer sur une courbe de
niveaux plus grande pour l’erreur
. Il arrive un moment où ce
point tangent est situé sur un des axes. Ensuite, ce point tangent est
situé de l’autre côté de l’axe et en annulant le coefficient
, on décroît à la fois
et
. Vérifions
numériquement sur une exemple en estimant les coefficients d’une
régression Lasso en deux dimensions
et en faisant varier la
paramètre
de la contrainte.
import warnings
from sklearn.metrics import mean_squared_error
import pandas
X = numpy.random.randn(100, 2) + 1.
X[:, 1] += 1.
y = numpy.sum(X, axis=1) + X[:, 1] + numpy.random.randn(100) / 10
def train_lasso(X, y, c):
with warnings.catch_warnings():
warnings.simplefilter("ignore")
lasso = Lasso(c, fit_intercept=False)
lasso.fit(X, y)
Er = mean_squared_error(y, lasso.predict(X))
El = numpy.abs(lasso.coef_).sum() * c
return Er, El, lasso.coef_
obs = []
for i in tqdm(range(0, 61)):
c = i / 4.
Er, El, coef = train_lasso(X, y, c)
obs.append(dict(c=c, Er=Er, El=El, E=Er+El, a1=coef[0], a2=coef[1]))
df = pandas.DataFrame(obs).set_index('c')
fig, ax = plt.subplots(1, 4, figsize=(14, 4))
ax[0].plot(X[:, 0], X[:, 1], '.', label='X')
ax[0].set_title("Features"); ax[0].set_xlabel("x1"); ax[0].set_ylabel("x2")
df[["Er", "El", "E"]].plot(ax=ax[1])
ax[1].set_title("Errors"); ax[1].set_xlabel("lambda"); ax[1].set_ylabel("Errors")
df.plot.scatter(x="a1", y="a2", ax=ax[2])
ax[2].set_title("Coefficients de la régression")
ax[2].set_xlabel("a1"); ax[2].set_ylabel("a2"); df[["a1", "a2"]].plot(ax=ax[3])
ax[3].set_title("Coefficients"); ax[3].set_xlabel("lambda"); ax[3].set_ylabel("Coefficients");
100%|██████████| 61/61 [00:00<00:00, 911.40it/s]
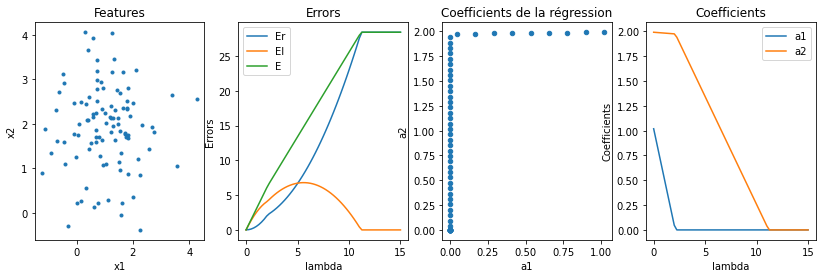
On retrouve numériquement le résultat énoncé ci-dessus.
Validation croisée et API scikit-learn#
La validation croisée est simple à faire dans scikit-learn est simple à faire si le modèle suit l’API de scikit-learn mais ce n’est pas le cas avec notre nouveau modèle. C’est pourtant essentiel pour s’assurer que le modèle est robuste. Toutefois scikit-learn permet de créer de nouveau modèle à la sauce sciki-learn.
from sklearn.base import BaseEstimator, RegressorMixin
class LassoRandomForestRegressor(BaseEstimator, RegressorMixin):
def __init__(self,
# Lasso
alpha=1.0, fit_intercept=True,
precompute=False, copy_X=True, max_iter=1000,
tol=1e-4, warm_start_lasso=False, positive=False,
random_state=None, selection='cyclic',
# RF
n_estimators=100,
criterion="squared_error",
max_depth=None,
min_samples_split=2,
min_samples_leaf=1,
min_weight_fraction_leaf=0.,
max_features=1.0,
max_leaf_nodes=None,
min_impurity_decrease=0.,
bootstrap=True,
oob_score=False,
n_jobs=None,
# random_state=None,
verbose=0,
warm_start_rf=False,
ccp_alpha=0.0,
max_samples=None):
# Lasso
self.alpha = alpha
self.fit_intercept = fit_intercept
self.precompute = precompute
self.copy_X = copy_X
self.max_iter = max_iter
self.tol = tol
self.warm_start_lasso = warm_start_lasso
self.positive = positive
self.random_state = random_state
self.selection = selection
# RF
self.n_estimators = n_estimators
self.criterion = criterion
self.max_depth = max_depth
self.min_samples_split = min_samples_split
self.min_samples_leaf = min_samples_leaf
self.min_weight_fraction_leaf = min_weight_fraction_leaf
self.max_features = max_features
self.max_leaf_nodes = max_leaf_nodes
self.min_impurity_decrease = min_impurity_decrease
self.bootstrap = bootstrap
self.oob_score = oob_score
self.n_jobs = n_jobs
self.random_state = random_state
self.verbose = verbose
self.warm_start_rf = warm_start_rf
self.ccp_alpha = ccp_alpha
self.max_samples = max_samples
def _concatenate_prediction(self, X):
preds = []
for i in range(len(self.rf_.estimators_)):
pred = self.rf_.estimators_[i].predict(X)
preds.append(pred)
return numpy.vstack(preds).T
def fit(self, X, y, sample_weight=None):
self.rf_ = RandomForestRegressor(
n_estimators=self.n_estimators, criterion=self.criterion,
max_depth=self.max_depth, min_samples_split=self.min_samples_split,
min_samples_leaf=self.min_samples_leaf,
min_weight_fraction_leaf=self.min_weight_fraction_leaf,
max_features=self.max_features, max_leaf_nodes=self.max_leaf_nodes,
min_impurity_decrease=self.min_impurity_decrease,
bootstrap=self.bootstrap,
oob_score=self.oob_score, n_jobs=self.n_jobs,
random_state=self.random_state, verbose=self.verbose,
warm_start=self.warm_start_rf, ccp_alpha=self.ccp_alpha,
max_samples=self.max_samples)
self.rf_.fit(X, y, sample_weight=sample_weight)
X_rf = self._concatenate_prediction(X)
self.lasso_ = Lasso(
alpha=self.alpha, max_iter=self.max_iter, fit_intercept=self.fit_intercept,
precompute=self.precompute, copy_X=self.copy_X,
tol=self.tol, warm_start=self.warm_start_lasso, positive=self.positive,
random_state=self.random_state, selection=self.selection)
self.lasso_.fit(X_rf, y)
return self
def predict(self, X):
X_rf = self._concatenate_prediction(X)
return self.lasso_.predict(X_rf)
model = LassoRandomForestRegressor(
alpha=1, n_estimators=100, max_iter=10000)
model.fit(X_train, y_train)
pred = model.predict(X_test)
r2_score(y_test, pred)
0.3841390522646667
Et la validation croisée fut :
from sklearn.model_selection import cross_val_score
cross_val_score(model, X_train, y_train, cv=5)
array([0.31294816, 0.26692181, 0.18796265, 0.48570352, 0.42128474])
Ce n’est pas très robuste. Peut-être est-ce dû à l’ordre des données (un léger effet temporel).
from sklearn.model_selection import ShuffleSplit
cross_val_score(LassoRandomForestRegressor(
n_estimators=100, alpha=10, max_iter=10000),
X_train, y_train, cv=ShuffleSplit(5))
array([0.03752275, 0.09378697, 0.62111807, 0.25086784, 0.33115676])
Pas beaucoup mieux. Le modèle n’est pas très robuste.
On essaye néanmoins de trouver les meilleurs paramètres à l’aide d’une grille de recherche.
from sklearn.model_selection import GridSearchCV
params = {'alpha': [0.1, 0.5, 1., 2., 5., 10],
'n_estimators': [10, 20, 50, 100],
'max_iter': [10000]
}
grid = GridSearchCV(LassoRandomForestRegressor(),
param_grid=params, verbose=1)
grid.fit(X_train, y_train)
Fitting 5 folds for each of 24 candidates, totalling 120 fits
GridSearchCV(estimator=LassoRandomForestRegressor(),
param_grid={'alpha': [0.1, 0.5, 1.0, 2.0, 5.0, 10],
'max_iter': [10000],
'n_estimators': [10, 20, 50, 100]},
verbose=1)In a Jupyter environment, please rerun this cell to show the HTML representation or trust the notebook. On GitHub, the HTML representation is unable to render, please try loading this page with nbviewer.org.
GridSearchCV(estimator=LassoRandomForestRegressor(),
param_grid={'alpha': [0.1, 0.5, 1.0, 2.0, 5.0, 10],
'max_iter': [10000],
'n_estimators': [10, 20, 50, 100]},
verbose=1)LassoRandomForestRegressor()
LassoRandomForestRegressor()
grid.best_params_
{'alpha': 10, 'max_iter': 10000, 'n_estimators': 100}
r2_score(y_test, grid.best_estimator_.predict(X_test))
0.44050616312634516
sum(grid.best_estimator_.lasso_.coef_ == 0)
63
On a réussi à supprimer 27 arbres.
Optimisation mémoire#
Le modèle précédent n’est pas optimal dans le sens où il stocke en mémoire tous les arbres, mêmes ceux associés à un coefficient nuls après la régression Lasso alors que le calcul ne sert à rien puisque ignoré.
class OptimizedLassoRandomForestRegressor(BaseEstimator, RegressorMixin):
def __init__(self,
# Lasso
alpha=1.0, fit_intercept=True,
precompute=False, copy_X=True, max_iter=1000,
tol=1e-4, warm_start_lasso=False, positive=False,
random_state=None, selection='cyclic',
# RF
n_estimators=100,
criterion="squared_error",
max_depth=None,
min_samples_split=2,
min_samples_leaf=1,
min_weight_fraction_leaf=0.,
max_features=1.0,
max_leaf_nodes=None,
min_impurity_decrease=0.,
bootstrap=True,
oob_score=False,
n_jobs=None,
# random_state=None,
verbose=0,
warm_start_rf=False,
ccp_alpha=0.0,
max_samples=None):
# Lasso
self.alpha = alpha
self.fit_intercept = fit_intercept
self.precompute = precompute
self.copy_X = copy_X
self.max_iter = max_iter
self.tol = tol
self.warm_start_lasso = warm_start_lasso
self.positive = positive
self.random_state = random_state
self.selection = selection
# RF
self.n_estimators = n_estimators
self.criterion = criterion
self.max_depth = max_depth
self.min_samples_split = min_samples_split
self.min_samples_leaf = min_samples_leaf
self.min_weight_fraction_leaf = min_weight_fraction_leaf
self.max_features = max_features
self.max_leaf_nodes = max_leaf_nodes
self.min_impurity_decrease = min_impurity_decrease
self.bootstrap = bootstrap
self.oob_score = oob_score
self.n_jobs = n_jobs
self.random_state = random_state
self.verbose = verbose
self.warm_start_rf = warm_start_rf
self.ccp_alpha = ccp_alpha
self.max_samples = max_samples
def _concatenate_prediction(self, X):
preds = []
for i in range(len(self.rf_.estimators_)):
pred = self.rf_.estimators_[i].predict(X)
preds.append(pred)
return numpy.vstack(preds).T
def fit(self, X, y, sample_weight=None):
self.rf_ = RandomForestRegressor(
n_estimators=self.n_estimators, criterion=self.criterion,
max_depth=self.max_depth, min_samples_split=self.min_samples_split,
min_samples_leaf=self.min_samples_leaf,
min_weight_fraction_leaf=self.min_weight_fraction_leaf,
max_features=self.max_features, max_leaf_nodes=self.max_leaf_nodes,
min_impurity_decrease=self.min_impurity_decrease,
bootstrap=self.bootstrap,
oob_score=self.oob_score, n_jobs=self.n_jobs,
random_state=self.random_state, verbose=self.verbose,
warm_start=self.warm_start_rf, ccp_alpha=self.ccp_alpha,
max_samples=self.max_samples)
self.rf_.fit(X, y, sample_weight=sample_weight)
X_rf = self._concatenate_prediction(X)
self.lasso_ = Lasso(
alpha=self.alpha, max_iter=self.max_iter, fit_intercept=self.fit_intercept,
precompute=self.precompute, copy_X=self.copy_X,
tol=self.tol, warm_start=self.warm_start_lasso, positive=self.positive,
random_state=self.random_state, selection=self.selection)
self.lasso_.fit(X_rf, y)
# on ne garde que les arbres associées à des coefficients non nuls
self.coef_ = []
self.intercept_ = self.lasso_.intercept_
self.estimators_ = []
for i in range(len(self.rf_.estimators_)):
if self.lasso_.coef_[i] != 0:
self.estimators_.append(self.rf_.estimators_[i])
self.coef_.append(self.lasso_.coef_[i])
self.coef_ = numpy.array(self.coef_)
del self.lasso_
del self.rf_
return self
def predict(self, X):
preds = []
for i in range(len(self.estimators_)):
pred = self.estimators_[i].predict(X)
preds.append(pred)
x_rf = numpy.vstack(preds).T
return x_rf @ self.coef_ + self.intercept_
model2 = OptimizedLassoRandomForestRegressor()
model2.fit(X_train, y_train)
pred = model2.predict(X_test)
r2_score(y_test, pred)
0.4215129880168422
Le modèle produit bien les mêmes résultats. Vérifions que le nouveau modèle prend moins de place une fois enregistré sur le disque.
import pickle
with open("optimzed_rf.pickle", "wb") as f:
pickle.dump(model2, f)
with open("optimzed_rf.pickle", "rb") as f:
model2 = pickle.load(f)
r2_score(y_test, model2.predict(X_test))
0.4215129880168422
with open("lasso_rf.pickle", "wb") as f:
pickle.dump(model, f)
import os
os.stat("optimzed_rf.pickle").st_size, os.stat("lasso_rf.pickle").st_size
(1280263, 2665081)
C’est bien le cas.