Note
Click here to download the full example code
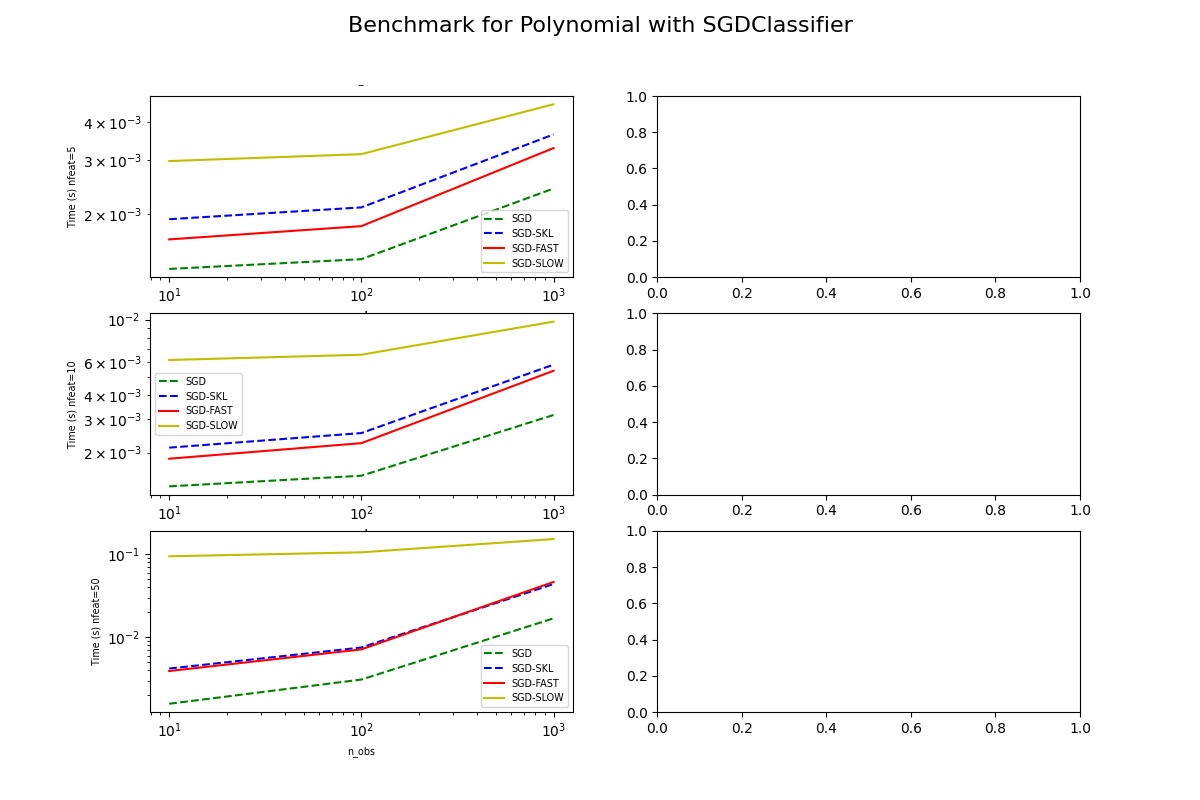
Benchmark of PolynomialFeatures + partialfit of SGDClassifier (standalone)¶
This benchmark looks into a new implementation of PolynomialFeatures proposed in PR13290. It tests the following configurations:
SGD: sklearn.linear_model.SGDClassifier only
SGD-SKL: sklearn.preprocessing.PolynomialFeatures from scikit-learn (no matter what it is)
SGD-FAST: new implementation copy-pasted in the benchmark source file
SGD-SLOW: implementation of 0.20.2 copy-pasted in the benchmark source file
This script is standalone and does not require pymlbenchmark as opposed to Benchmark of PolynomialFeatures + partialfit of SGDClassifier which reuse functions implemented in pymlbenchmark.
from time import perf_counter as time
import numpy
import numpy as np
from numpy.random import rand
import matplotlib.pyplot as plt
import pandas
import sklearn
from sklearn.pipeline import make_pipeline
from sklearn.preprocessing import PolynomialFeatures
from sklearn.linear_model import SGDClassifier
try:
from sklearn.utils._testing import ignore_warnings
except ImportError:
from sklearn.utils.testing import ignore_warnings
from mlinsights.mlmodel import ExtendedFeatures
Implementations to benchmark¶
def fcts_model(X, y):
model1 = SGDClassifier()
model2 = make_pipeline(PolynomialFeatures(), SGDClassifier())
model3 = make_pipeline(ExtendedFeatures(kind='poly'), SGDClassifier())
model4 = make_pipeline(ExtendedFeatures(kind='poly-slow'), SGDClassifier())
model1.fit(PolynomialFeatures().fit_transform(X), y)
model2.fit(X, y)
model3.fit(X, y)
model4.fit(X, y)
def partial_fit_model1(X, y, model=model1):
return model.partial_fit(X, y)
def partial_fit_model2(X, y, model=model2):
X2 = model.steps[0][1].transform(X)
return model.steps[1][1].partial_fit(X2, y)
def partial_fit_model3(X, y, model=model3):
X2 = model.steps[0][1].transform(X)
return model.steps[1][1].partial_fit(X2, y)
def partial_fit_model4(X, y, model=model4):
X2 = model.steps[0][1].transform(X)
return model.steps[1][1].partial_fit(X2, y)
return (partial_fit_model1, partial_fit_model2,
partial_fit_model3, partial_fit_model4)
Benchmarks¶
def build_x_y(ntrain, nfeat):
X_train = np.empty((ntrain, nfeat))
X_train[:, :] = rand(ntrain, nfeat)[:, :]
X_trainsum = X_train.sum(axis=1)
eps = rand(ntrain) - 0.5
X_trainsum_ = X_trainsum + eps
y_train = (X_trainsum_ >= X_trainsum).ravel().astype(int)
return X_train, y_train
@ignore_warnings(category=(FutureWarning, DeprecationWarning))
def bench(n_obs, n_features, repeat=1000, verbose=False):
res = []
for n in n_obs:
for nfeat in n_features:
X_train, y_train = build_x_y(1000, nfeat)
obs = dict(n_obs=n, nfeat=nfeat)
fct1, fct2, fct3, fct4 = fcts_model(X_train, y_train)
# creates different inputs to avoid caching in any ways
Xs = []
Xpolys = []
for r in range(repeat):
X, y = build_x_y(n, nfeat)
Xs.append((X, y))
Xpolys.append((PolynomialFeatures().fit_transform(X), y))
# measure fct1
r = len(Xs)
st = time()
for X, y in Xpolys:
fct1(X, y)
end = time()
obs["time_sgd"] = (end - st) / r
res.append(obs)
# measures fct2
st = time()
for X, y in Xs:
fct2(X, y)
end = time()
obs["time_pipe_skl"] = (end - st) / r
res.append(obs)
# measures fct3
st = time()
for X, y in Xs:
fct3(X, y)
end = time()
obs["time_pipe_fast"] = (end - st) / r
res.append(obs)
# measures fct4
st = time()
for X, y in Xs:
fct4(X, y)
end = time()
obs["time_pipe_slow"] = (end - st) / r
res.append(obs)
if verbose and (len(res) % 1 == 0 or n >= 10000):
print("bench", len(res), ":", obs)
return res
Plots¶
def plot_results(df, verbose=False):
nrows = max(len(set(df.nfeat)), 2)
ncols = max(1, 2)
fig, ax = plt.subplots(nrows, ncols,
figsize=(nrows * 4, ncols * 4))
colors = "gbry"
row = 0
for nfeat in sorted(set(df.nfeat)):
pos = 0
for _ in range(1):
a = ax[row, pos]
if row == ax.shape[0] - 1:
a.set_xlabel("N observations", fontsize='x-small')
if pos == 0:
a.set_ylabel("Time (s) nfeat={}".format(nfeat),
fontsize='x-small')
subset = df[df.nfeat == nfeat]
if subset.shape[0] == 0:
continue
subset = subset.sort_values("n_obs")
if verbose:
print(subset)
label = "SGD"
subset.plot(x="n_obs", y="time_sgd", label=label, ax=a,
logx=True, logy=True, c=colors[0], style='--')
label = "SGD-SKL"
subset.plot(x="n_obs", y="time_pipe_skl", label=label, ax=a,
logx=True, logy=True, c=colors[1], style='--')
label = "SGD-FAST"
subset.plot(x="n_obs", y="time_pipe_fast", label=label, ax=a,
logx=True, logy=True, c=colors[2])
label = "SGD-SLOW"
subset.plot(x="n_obs", y="time_pipe_slow", label=label, ax=a,
logx=True, logy=True, c=colors[3])
a.legend(loc=0, fontsize='x-small')
if row == 0:
a.set_title("--", fontsize='x-small')
pos += 1
row += 1
plt.suptitle("Benchmark for Polynomial with SGDClassifier", fontsize=16)
Final function for the benchmark¶
def run_bench(repeat=100, verbose=False):
n_obs = [10, 100, 1000]
n_features = [5, 10, 50]
with sklearn.config_context(assume_finite=True):
start = time()
results = bench(n_obs, n_features, repeat=repeat, verbose=verbose)
end = time()
results_df = pandas.DataFrame(results)
print("Total time = %0.3f sec\n" % (end - start))
# plot the results
plot_results(results_df, verbose=verbose)
return results_df
Run the benchmark¶
print("numpy:", numpy.__version__)
print("scikit-learn:", sklearn.__version__)
df = run_bench(verbose=True)
print(df)
plt.show()
numpy: 1.23.5
scikit-learn: 1.2.1
bench 4 : {'n_obs': 10, 'nfeat': 5, 'time_sgd': 0.0013249226997140795, 'time_pipe_skl': 0.0019261512299999595, 'time_pipe_fast': 0.001654766010469757, 'time_pipe_slow': 0.0029830967797897755}
bench 8 : {'n_obs': 10, 'nfeat': 10, 'time_sgd': 0.0013282932701986284, 'time_pipe_skl': 0.002122467309818603, 'time_pipe_fast': 0.0018563237501075492, 'time_pipe_slow': 0.006132730239769444}
bench 12 : {'n_obs': 10, 'nfeat': 50, 'time_sgd': 0.001581792570068501, 'time_pipe_skl': 0.0042063837201567365, 'time_pipe_fast': 0.003923654420068487, 'time_pipe_slow': 0.0948916418699082}
bench 16 : {'n_obs': 100, 'nfeat': 5, 'time_sgd': 0.0014259226596914233, 'time_pipe_skl': 0.002105059499735944, 'time_pipe_fast': 0.0018281825300073252, 'time_pipe_slow': 0.003142296050209552}
bench 20 : {'n_obs': 100, 'nfeat': 10, 'time_sgd': 0.0015108765999320894, 'time_pipe_skl': 0.0025323338998714463, 'time_pipe_fast': 0.0022405518998857587, 'time_pipe_slow': 0.006537817390053533}
bench 24 : {'n_obs': 100, 'nfeat': 50, 'time_sgd': 0.003097828699974343, 'time_pipe_skl': 0.007540988689870573, 'time_pipe_fast': 0.007151761099812574, 'time_pipe_slow': 0.10592318902025}
bench 28 : {'n_obs': 1000, 'nfeat': 5, 'time_sgd': 0.002426280700019561, 'time_pipe_skl': 0.0036441037902841342, 'time_pipe_fast': 0.0032889807398896664, 'time_pipe_slow': 0.004574504140182398}
bench 32 : {'n_obs': 1000, 'nfeat': 10, 'time_sgd': 0.0031518084503477438, 'time_pipe_skl': 0.0057958847098052504, 'time_pipe_fast': 0.005382269050460309, 'time_pipe_slow': 0.009759210420306773}
bench 36 : {'n_obs': 1000, 'nfeat': 50, 'time_sgd': 0.016945749250007792, 'time_pipe_skl': 0.04391203346021939, 'time_pipe_fast': 0.0465518391598016, 'time_pipe_slow': 0.15311013977974652}
Total time = 73.642 sec
n_obs nfeat time_sgd time_pipe_skl time_pipe_fast time_pipe_slow
0 10 5 0.001325 0.001926 0.001655 0.002983
1 10 5 0.001325 0.001926 0.001655 0.002983
2 10 5 0.001325 0.001926 0.001655 0.002983
3 10 5 0.001325 0.001926 0.001655 0.002983
12 100 5 0.001426 0.002105 0.001828 0.003142
13 100 5 0.001426 0.002105 0.001828 0.003142
14 100 5 0.001426 0.002105 0.001828 0.003142
15 100 5 0.001426 0.002105 0.001828 0.003142
24 1000 5 0.002426 0.003644 0.003289 0.004575
25 1000 5 0.002426 0.003644 0.003289 0.004575
26 1000 5 0.002426 0.003644 0.003289 0.004575
27 1000 5 0.002426 0.003644 0.003289 0.004575
n_obs nfeat time_sgd time_pipe_skl time_pipe_fast time_pipe_slow
4 10 10 0.001328 0.002122 0.001856 0.006133
5 10 10 0.001328 0.002122 0.001856 0.006133
6 10 10 0.001328 0.002122 0.001856 0.006133
7 10 10 0.001328 0.002122 0.001856 0.006133
16 100 10 0.001511 0.002532 0.002241 0.006538
17 100 10 0.001511 0.002532 0.002241 0.006538
18 100 10 0.001511 0.002532 0.002241 0.006538
19 100 10 0.001511 0.002532 0.002241 0.006538
28 1000 10 0.003152 0.005796 0.005382 0.009759
29 1000 10 0.003152 0.005796 0.005382 0.009759
30 1000 10 0.003152 0.005796 0.005382 0.009759
31 1000 10 0.003152 0.005796 0.005382 0.009759
n_obs nfeat time_sgd time_pipe_skl time_pipe_fast time_pipe_slow
8 10 50 0.001582 0.004206 0.003924 0.094892
9 10 50 0.001582 0.004206 0.003924 0.094892
10 10 50 0.001582 0.004206 0.003924 0.094892
11 10 50 0.001582 0.004206 0.003924 0.094892
20 100 50 0.003098 0.007541 0.007152 0.105923
21 100 50 0.003098 0.007541 0.007152 0.105923
22 100 50 0.003098 0.007541 0.007152 0.105923
23 100 50 0.003098 0.007541 0.007152 0.105923
32 1000 50 0.016946 0.043912 0.046552 0.153110
33 1000 50 0.016946 0.043912 0.046552 0.153110
34 1000 50 0.016946 0.043912 0.046552 0.153110
35 1000 50 0.016946 0.043912 0.046552 0.153110
n_obs nfeat time_sgd time_pipe_skl time_pipe_fast time_pipe_slow
0 10 5 0.001325 0.001926 0.001655 0.002983
1 10 5 0.001325 0.001926 0.001655 0.002983
2 10 5 0.001325 0.001926 0.001655 0.002983
3 10 5 0.001325 0.001926 0.001655 0.002983
4 10 10 0.001328 0.002122 0.001856 0.006133
5 10 10 0.001328 0.002122 0.001856 0.006133
6 10 10 0.001328 0.002122 0.001856 0.006133
7 10 10 0.001328 0.002122 0.001856 0.006133
8 10 50 0.001582 0.004206 0.003924 0.094892
9 10 50 0.001582 0.004206 0.003924 0.094892
10 10 50 0.001582 0.004206 0.003924 0.094892
11 10 50 0.001582 0.004206 0.003924 0.094892
12 100 5 0.001426 0.002105 0.001828 0.003142
13 100 5 0.001426 0.002105 0.001828 0.003142
14 100 5 0.001426 0.002105 0.001828 0.003142
15 100 5 0.001426 0.002105 0.001828 0.003142
16 100 10 0.001511 0.002532 0.002241 0.006538
17 100 10 0.001511 0.002532 0.002241 0.006538
18 100 10 0.001511 0.002532 0.002241 0.006538
19 100 10 0.001511 0.002532 0.002241 0.006538
20 100 50 0.003098 0.007541 0.007152 0.105923
21 100 50 0.003098 0.007541 0.007152 0.105923
22 100 50 0.003098 0.007541 0.007152 0.105923
23 100 50 0.003098 0.007541 0.007152 0.105923
24 1000 5 0.002426 0.003644 0.003289 0.004575
25 1000 5 0.002426 0.003644 0.003289 0.004575
26 1000 5 0.002426 0.003644 0.003289 0.004575
27 1000 5 0.002426 0.003644 0.003289 0.004575
28 1000 10 0.003152 0.005796 0.005382 0.009759
29 1000 10 0.003152 0.005796 0.005382 0.009759
30 1000 10 0.003152 0.005796 0.005382 0.009759
31 1000 10 0.003152 0.005796 0.005382 0.009759
32 1000 50 0.016946 0.043912 0.046552 0.153110
33 1000 50 0.016946 0.043912 0.046552 0.153110
34 1000 50 0.016946 0.043912 0.046552 0.153110
35 1000 50 0.016946 0.043912 0.046552 0.153110
Total running time of the script: ( 1 minutes 20.040 seconds)