Séries temporelles et map reduce#
Links: notebook, html, PDF, python, slides, GitHub
Map/Reduce est un concept qui permet de distribuer les données facilement si elles sont indépendantes. C’est une condition qu’une série temporelle ne vérifie pas du fait de la dépendance temporelle. Voyons ce que cela change.
from jyquickhelper import add_notebook_menu
add_notebook_menu()
# Répare une incompatibilité entre scipy 1.0 et statsmodels 0.8.
from pymyinstall.fix import fix_scipy10_for_statsmodels08
fix_scipy10_for_statsmodels08()
On souhaite simplement calculer la dérivée de la série temporelle :
.
%matplotlib inline
Data#
from pyensae.finance import StockPrices
stock = StockPrices("MSFT", folder=".", url="yahoo")
stock.tail()
| Date | High | Low | Open | Close | Volume | Adj Close | |
|---|---|---|---|---|---|---|---|
| Date | |||||||
| 2020-12-24 | 2020-12-24 | 223.610001 | 221.199997 | 221.419998 | 222.750000 | 10550600.0 | 222.750000 |
| 2020-12-28 | 2020-12-28 | 226.029999 | 223.020004 | 224.449997 | 224.960007 | 17933500.0 | 224.960007 |
| 2020-12-29 | 2020-12-29 | 227.179993 | 223.580002 | 226.309998 | 224.149994 | 17403200.0 | 224.149994 |
| 2020-12-30 | 2020-12-30 | 225.630005 | 221.470001 | 225.229996 | 221.679993 | 20272300.0 | 221.679993 |
| 2020-12-31 | 2020-12-31 | 223.000000 | 219.679993 | 221.699997 | 222.419998 | 20926900.0 | 222.419998 |
On crée une colonne supplémentaire pour l’indice de la série
temporelle :
dt = stock.df()
dt = dt[["Close"]]
dt = dt.reset_index(drop=True)
data = dt
dt.tail()
| Close | |
|---|---|
| 5279 | 222.750000 |
| 5280 | 224.960007 |
| 5281 | 224.149994 |
| 5282 | 221.679993 |
| 5283 | 222.419998 |
La fonction shift rend le calcul très simple avec pandas.
data_pandas = data.copy()
data_pandas["Close2"] = data.shift(1)
data_pandas["delta"] = data_pandas["Close"] - data_pandas["Close2"]
data_pandas.tail()
| Close | Close2 | delta | |
|---|---|---|---|
| 5279 | 222.750000 | 221.020004 | 1.729996 |
| 5280 | 224.960007 | 222.750000 | 2.210007 |
| 5281 | 224.149994 | 224.960007 | -0.810013 |
| 5282 | 221.679993 | 224.149994 | -2.470001 |
| 5283 | 222.419998 | 221.679993 | 0.740005 |
La fonction est très rapide car elle utilise l’ordre des données et son index. Pour s’en passer, on ajoute une colonne qui contient l’index original puis on mélange pour simuler le fait qu’en map/reduce, l’ordre des informations n’est pas connu à l’avance.
import numpy
data = dt.reindex(numpy.random.permutation(data.index))
data = data.reset_index(drop=False)
data.columns = ["t", "close"]
data.tail()
| t | close | |
|---|---|---|
| 5279 | 4660 | 104.190002 |
| 5280 | 476 | 31.870001 |
| 5281 | 3522 | 36.910000 |
| 5282 | 2867 | 24.670000 |
| 5283 | 4348 | 65.480003 |
Dérivée avec pandas#
Le traitement de chaque ligne est indépendant et ne doit pas prendre en
compte aucune autre ligne mais on a besoin de pour
calculer
.
data["tt"] = data["t"] - 1
méthode efficace#
Lors d’une jointure, pandas va trier
chaque côté de la jointure par ordre croissant de clé. S’il y a
observations, cela a un coût de
, il réalise
ensuite une fusion des deux bases en ne considérant que les lignes
partageant la même clé. Cette façon de faire ne convient que lorsqu’on
fait une jointure avec une condition n’incluant que des ET logique et
des égalités.
join = data.merge(data, left_on="t", right_on="tt", suffixes=("", "2"))
join.tail()
| t | close | tt | t2 | close2 | tt2 | |
|---|---|---|---|---|---|---|
| 5278 | 4660 | 104.190002 | 4659 | 4661 | 105.430000 | 4660 |
| 5279 | 476 | 31.870001 | 475 | 477 | 31.400000 | 476 |
| 5280 | 3522 | 36.910000 | 3521 | 3523 | 36.130001 | 3522 |
| 5281 | 2867 | 24.670000 | 2866 | 2868 | 24.760000 | 2867 |
| 5282 | 4348 | 65.480003 | 4347 | 4349 | 65.389999 | 4348 |
derivee = join.copy()
derivee["derivee"] = derivee["close"] - derivee["close2"]
derivee.tail()
| t | close | tt | t2 | close2 | tt2 | derivee | |
|---|---|---|---|---|---|---|---|
| 5278 | 4660 | 104.190002 | 4659 | 4661 | 105.430000 | 4660 | -1.239998 |
| 5279 | 476 | 31.870001 | 475 | 477 | 31.400000 | 476 | 0.470001 |
| 5280 | 3522 | 36.910000 | 3521 | 3523 | 36.130001 | 3522 | 0.779999 |
| 5281 | 2867 | 24.670000 | 2866 | 2868 | 24.760000 | 2867 | -0.090000 |
| 5282 | 4348 | 65.480003 | 4347 | 4349 | 65.389999 | 4348 | 0.090004 |
En résumé :
new_data = data.copy()
new_data["tt"] = new_data["t"] + 1 # MAP
new_data = new_data.merge(new_data, left_on="t", right_on="tt", suffixes=("", "2")) # JOIN = SORT + MAP + REDUCE
new_data["derivee"] = new_data["close"] - new_data["close2"] # MAP
print(new_data.shape)
new_data.tail()
(5283, 7)
| t | close | tt | t2 | close2 | tt2 | derivee | |
|---|---|---|---|---|---|---|---|
| 5278 | 4660 | 104.190002 | 4661 | 4659 | 101.980003 | 4660 | 2.209999 |
| 5279 | 476 | 31.870001 | 477 | 475 | 32.570000 | 476 | -0.699999 |
| 5280 | 3522 | 36.910000 | 3523 | 3521 | 37.160000 | 3522 | -0.250000 |
| 5281 | 2867 | 24.670000 | 2868 | 2866 | 24.190001 | 2867 | 0.480000 |
| 5282 | 4348 | 65.480003 | 4349 | 4347 | 64.949997 | 4348 | 0.530006 |
mesure de coût#
La série n’est pas assez longue pour observer la relation entre le temps de calcul et le nombre d’observations.
def derive(data):
new_data = data.copy()
new_data["tt"] = new_data["t"] + 1 # MAP
new_data = new_data.merge(new_data, left_on="t", right_on="tt", suffixes=("", "2")) # JOIN = MAP + REDUCE
new_data["derivee"] = new_data["close"] - new_data["close2"] # MAP
return new_data
On choisit une régression linéaire de type
HuberRegressor
pour régresser . Ce
modèle est beaucoup moins sensible aux points aberrants que les autres
formes de régressions. On utilise cette régression avec le module
RobustLinearModels
du module statsmodels pour calculer les p-values
import time, pandas, numpy, sklearn.linear_model as lin
import matplotlib.pyplot as plt
import statsmodels.api as smapi
from random import randint
def graph_cout(data, h=100, nb=10, add_n2=False, derive=derive):
dh = len(data) // h
res = []
for n in range(max(dh, 500), len(data), dh):
df = data[0:n+randint(-10,10)]
mean = []
for i in range(0, nb):
t = time.perf_counter()
derive(df)
dt = time.perf_counter() - t
mean.append(dt)
res.append((n, mean[len(mean)//2]))
# stat
stat = pandas.DataFrame(res, columns=["N", "processing time"])
stat["logN"] = numpy.log(stat["N"]) / numpy.log(10)
stat["NlogN"] = stat["N"] * stat["logN"]
stat["N2"] = stat["N"] * stat["N"]
# statsmodels
stat["one"] = 1
X = stat[["logN", "N", "NlogN", "N2", "one"]]
if not add_n2:
X = X.drop("N2", axis=1)
rlm_model = smapi.RLM(stat["processing time"], X, M=smapi.robust.norms.HuberT())
rlm_results = rlm_model.fit()
yp = rlm_results.predict(X)
print(yp.shape, type(yp))
stat["smooth"] = yp
# graph
fig, ax = plt.subplots()
stat.plot(x="N", y=["processing time", "smooth"], ax=ax)
return ax, rlm_results
ax, results = graph_cout(data)
print(results.summary())
ax;
(92,) <class 'pandas.core.series.Series'>
Robust linear Model Regression Results
==============================================================================
Dep. Variable: processing time No. Observations: 92
Model: RLM Df Residuals: 88
Method: IRLS Df Model: 3
Norm: HuberT
Scale Est.: mad
Cov Type: H1
Date: Fri, 01 Jan 2021
Time: 03:27:54
No. Iterations: 50
==============================================================================
coef std err z P>|z| [0.025 0.975]
------------------------------------------------------------------------------
logN 0.0035 0.001 2.661 0.008 0.001 0.006
N -8.829e-06 2.77e-06 -3.191 0.001 -1.43e-05 -3.41e-06
NlogN 2.117e-06 6.56e-07 3.228 0.001 8.31e-07 3.4e-06
one -0.0049 0.003 -1.544 0.123 -0.011 0.001
==============================================================================
If the model instance has been used for another fit with different fit parameters, then the fit options might not be the correct ones anymore .
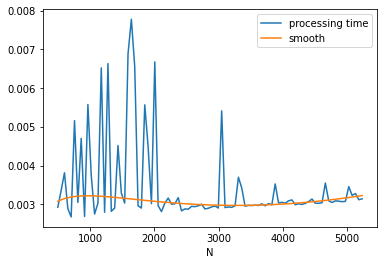
Le coût de l’algorithme est au moins linéaire. Cela signifie que le coût
du calcul qu’on cherche à mesurer est noyé dans plein d’autres choses
non négligeable. La valeur des coefficients n’indique pas grand chose
car les variables ,
évoluent sur des échelles
différentes.
N = 200000
from random import random
data2 = pandas.DataFrame({"t":range(0,N), "close": [random() for i in range(0, N)]})
ax, stats = graph_cout(data2, h=25)
print(stats.summary())
ax;
(24,) <class 'pandas.core.series.Series'>
Robust linear Model Regression Results
==============================================================================
Dep. Variable: processing time No. Observations: 24
Model: RLM Df Residuals: 20
Method: IRLS Df Model: 3
Norm: HuberT
Scale Est.: mad
Cov Type: H1
Date: Fri, 01 Jan 2021
Time: 03:28:04
No. Iterations: 47
==============================================================================
coef std err z P>|z| [0.025 0.975]
------------------------------------------------------------------------------
logN -0.0396 0.017 -2.327 0.020 -0.073 -0.006
N 5.63e-06 1.75e-06 3.213 0.001 2.2e-06 9.06e-06
NlogN -9.342e-07 3.08e-07 -3.036 0.002 -1.54e-06 -3.31e-07
one 0.1434 0.064 2.232 0.026 0.017 0.269
==============================================================================
If the model instance has been used for another fit with different fit parameters, then the fit options might not be the correct ones anymore .
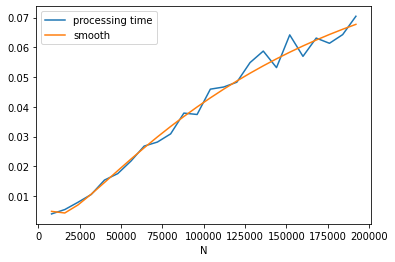
Les résultats sont assez volatiles. Il faut regarder les intervalles de confiance et regarder lesquels n’incluent pas 0.
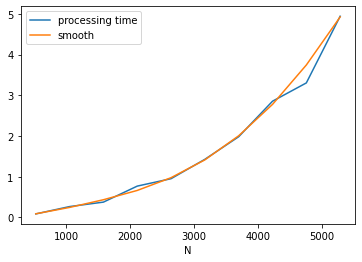
méthode inefficace#
Dans ce cas, on fait un produit en croix de toutes les lignes de la
bases avec elles-même puis on filtre le résultat pour ne garder que les
lignes qui vérifient la condition souhaitée quelle qu’elle soit. Le
temps d’exécution est en et la différence est vite
significative.
new_data2 = data.copy()
new_data2["tt"] = new_data2["t"] + 1 # MAP
new_data2["key"] = 1
new_data2 = new_data2.merge(new_data2, on="key", suffixes=("", "2")) # JOIN = MAP^2
new_data2.shape
(27920656, 7)
mapind = new_data2.t == new_data2.t2
new_data2 = new_data2[mapind] # MAP
new_data2.shape
(5284, 7)
new_data2["derivee"] = new_data2["t"] - new_data2["t2"] # MAP
new_data2.tail()
| t | close | tt | key | t2 | close2 | tt2 | derivee | |
|---|---|---|---|---|---|---|---|---|
| 27899515 | 4660 | 104.190002 | 4661 | 1 | 4660 | 104.190002 | 4661 | 0 |
| 27904800 | 476 | 31.870001 | 477 | 1 | 476 | 31.870001 | 477 | 0 |
| 27910085 | 3522 | 36.910000 | 3523 | 1 | 3522 | 36.910000 | 3523 | 0 |
| 27915370 | 2867 | 24.670000 | 2868 | 1 | 2867 | 24.670000 | 2868 | 0 |
| 27920655 | 4348 | 65.480003 | 4349 | 1 | 4348 | 65.480003 | 4349 | 0 |
mesure de coût inefficace#
def derive_inefficace(data):
new_data2 = data.copy()
new_data2["tt"] = new_data2["t"] + 1
new_data2["key"] = 1
new_data2 = new_data2.merge(new_data2, on="key", suffixes=("", "2"))
new_data2 = new_data2[new_data2.t == new_data2.t2]
new_data2["derivee"] = new_data2["t"] - new_data2["t2"] # MAP
return new_data2
ax, stats = graph_cout(data, h=10, nb=5, derive=derive_inefficace, add_n2=True)
print(stats.summary())
ax;
(10,) <class 'pandas.core.series.Series'>
Robust linear Model Regression Results
==============================================================================
Dep. Variable: processing time No. Observations: 10
Model: RLM Df Residuals: 5
Method: IRLS Df Model: 4
Norm: HuberT
Scale Est.: mad
Cov Type: H1
Date: Fri, 01 Jan 2021
Time: 03:29:44
No. Iterations: 50
==============================================================================
coef std err z P>|z| [0.025 0.975]
------------------------------------------------------------------------------
logN -3.5525 6.675 -0.532 0.595 -16.635 9.530
N 0.0226 0.027 0.837 0.403 -0.030 0.076
NlogN -0.0064 0.007 -0.889 0.374 -0.021 0.008
N2 6.411e-07 3.49e-07 1.836 0.066 -4.32e-08 1.33e-06
one 6.8518 14.218 0.482 0.630 -21.015 34.718
==============================================================================
If the model instance has been used for another fit with different fit parameters, then the fit options might not be the correct ones anymore .
avec des itérateurs#
version efficace#
rows = data[["t", "close"]].itertuples()
list(rows)[:2]
[Pandas(Index=0, t=1726, close=29.350000381469727),
Pandas(Index=1, t=1244, close=27.11000061035156)]
rows = data[["t", "close"]].itertuples()
rows = map(lambda r: (r.t, r.close, r.t+1), rows)
list(rows)[:2]
[(1726, 29.350000381469727, 1727), (1244, 27.11000061035156, 1245)]
import copy
from cytoolz.itertoolz import join
def get_iterrows():
rows_as_tuple = data[["t", "close"]].itertuples()
rows = map(lambda r: (r.t, r.close, r.t+1), rows_as_tuple)
return rows
rows1 = get_iterrows()
rows2 = get_iterrows()
rows = join(lambda t: t[2], rows1, lambda t: t[0], rows2)
rows = map(lambda tu: tu[0] + tu[1], rows)
rows = map(lambda row: (row[0], row[4] - row[1]), rows)
results = list(rows)
results[:4]
[(1725, 0.1100006103515625),
(1243, -0.11999893188476918),
(3128, -0.75),
(4095, 0.29000091552734375)]
version inefficace#
La méthode inefficace avec pandas est particulièrement inefficace car
elle nécessite de stocker un tableau intermédiaire qui contient
lignes.
import copy
from cytoolz.itertoolz import join
def get_iterrows():
rows_as_tuple = data[["t", "close"]].itertuples()
rows = map(lambda r: (r.t, r.close, r.t+1, 1), rows_as_tuple) # on ajoute 1
return rows
rows1 = get_iterrows()
rows2 = get_iterrows()
rows = join(lambda t: t[-1], rows1, lambda t: t[-1], rows2) # on fait un produit croisé
rows = map(lambda tu: tu[0] + tu[1], rows)
rows = filter(lambda t: t[2] == t[4], rows) # on filtre les lignes qui nous intéresse
rows = map(lambda row: (row[0], row[5] - row[1]), rows)
results = list(rows) # c'est très lent
results[:4]
[(1725, 0.1100006103515625),
(1243, -0.11999893188476918),
(3128, -0.75),
(4095, 0.29000091552734375)]
avec SQL#
conversion du dataframe au format SQL#
data = stock.df()
data.columns = [_.replace(" ", "_") for _ in data.columns]
data = data.reset_index(drop=True).reset_index(drop=False)
data.columns = ["t"] + list(data.columns[1:])
data.head()
| t | Date | High | Low | Open | Close | Volume | Adj_Close | |
|---|---|---|---|---|---|---|---|---|
| 0 | 0 | 2000-01-03 | 59.3125 | 56.00000 | 58.68750 | 58.28125 | 53228400.0 | 37.102634 |
| 1 | 1 | 2000-01-04 | 58.5625 | 56.12500 | 56.78125 | 56.31250 | 54119000.0 | 35.849308 |
| 2 | 2 | 2000-01-05 | 58.1875 | 54.68750 | 55.56250 | 56.90625 | 64059600.0 | 36.227283 |
| 3 | 3 | 2000-01-06 | 56.9375 | 54.18750 | 56.09375 | 55.00000 | 54976600.0 | 35.013741 |
| 4 | 4 | 2000-01-07 | 56.1250 | 53.65625 | 54.31250 | 55.71875 | 62013600.0 | 35.471302 |
import sqlite3
con = sqlite3.connect(":memory:")
tbl = data.to_sql("stock", con, index=False)
%load_ext pyensae
%SQL_tables -v con
['stock']
%%SQL -v con
SELECT * FROM stock LIMIT 5
| t | Date | High | Low | Open | Close | Volume | Adj_Close | |
|---|---|---|---|---|---|---|---|---|
| 0 | 0 | 2000-01-03 | 59.3125 | 56.00000 | 58.68750 | 58.28125 | 53228400.0 | 37.102634 |
| 1 | 1 | 2000-01-04 | 58.5625 | 56.12500 | 56.78125 | 56.31250 | 54119000.0 | 35.849308 |
| 2 | 2 | 2000-01-05 | 58.1875 | 54.68750 | 55.56250 | 56.90625 | 64059600.0 | 36.227283 |
| 3 | 3 | 2000-01-06 | 56.9375 | 54.18750 | 56.09375 | 55.00000 | 54976600.0 | 35.013741 |
| 4 | 4 | 2000-01-07 | 56.1250 | 53.65625 | 54.31250 | 55.71875 | 62013600.0 | 35.471302 |
version efficace#
L’instruction ON précise sur quelle ou quelles colonnes opérer la
fusion.
%%SQL -v con
SELECT A.t AS t, A.Close AS Close, A.tt AS tt,
B.t AS t2, B.Close AS Close2, B.tt AS tt2
FROM (
SELECT t, Close, t+1 AS tt FROM stock
) AS A
INNER JOIN (
SELECT t, Close, t+1 AS tt FROM stock
) AS B
ON A.tt == B.t
| t | Close | tt | t2 | Close2 | tt2 | |
|---|---|---|---|---|---|---|
| 0 | 0 | 58.28125 | 1 | 1 | 56.31250 | 2 |
| 1 | 1 | 56.31250 | 2 | 2 | 56.90625 | 3 |
| 2 | 2 | 56.90625 | 3 | 3 | 55.00000 | 4 |
| 3 | 3 | 55.00000 | 4 | 4 | 55.71875 | 5 |
| 4 | 4 | 55.71875 | 5 | 5 | 56.12500 | 6 |
| 5 | 5 | 56.12500 | 6 | 6 | 54.68750 | 7 |
| 6 | 6 | 54.68750 | 7 | 7 | 52.90625 | 8 |
| 7 | 7 | 52.90625 | 8 | 8 | 53.90625 | 9 |
| 8 | 8 | 53.90625 | 9 | 9 | 56.12500 | 10 |
| 9 | 9 | 56.12500 | 10 | 10 | 57.65625 | 11 |
version inefficace#
Pour la version inefficace, l’instruction JOIN effectue tous les
combinaisons de lignes possibles, soit . Le mot-clé
WHERE
garde les couples de lignes qui nous intéresse.
%%SQL -v con
SELECT A.t AS t, A.Close AS Close, A.tt AS tt,
B.t AS t2, B.Close AS Close2, B.tt AS tt2
FROM (
SELECT t, Close, t+1 AS tt FROM stock
) AS A
INNER JOIN (
SELECT t, Close, t+1 AS tt FROM stock
) AS B
WHERE A.tt >= B.t AND A.tt <= B.t -- on écrit l'égalité comme ceci pour contourner les optimisations
-- réalisée par SQLlite
| t | Close | tt | t2 | Close2 | tt2 | |
|---|---|---|---|---|---|---|
| 0 | 0 | 58.28125 | 1 | 1 | 56.31250 | 2 |
| 1 | 1 | 56.31250 | 2 | 2 | 56.90625 | 3 |
| 2 | 2 | 56.90625 | 3 | 3 | 55.00000 | 4 |
| 3 | 3 | 55.00000 | 4 | 4 | 55.71875 | 5 |
| 4 | 4 | 55.71875 | 5 | 5 | 56.12500 | 6 |
| 5 | 5 | 56.12500 | 6 | 6 | 54.68750 | 7 |
| 6 | 6 | 54.68750 | 7 | 7 | 52.90625 | 8 |
| 7 | 7 | 52.90625 | 8 | 8 | 53.90625 | 9 |
| 8 | 8 | 53.90625 | 9 | 9 | 56.12500 | 10 |
| 9 | 9 | 56.12500 | 10 | 10 | 57.65625 | 11 |