Float conversion#
Links: notebook, html, PDF, python, slides, GitHub
I came up with the following question
?
What is the probability this holds?
from jyquickhelper import add_notebook_menu
add_notebook_menu()
%matplotlib inline
Probability (float64)x == (float32)x#
Let’s evaluate how many time we draw a random double number equal to its float conversion.
import numpy
rnd = numpy.random.random(100000000)
rnd.shape, rnd.dtype
((100000000,), dtype('float64'))
rnd32 = rnd.astype(numpy.float32).astype(numpy.float64)
equal = (rnd == rnd32).sum()
equal
2
It is very low. Let’s check the reverse is true.
rnd32b = rnd32.astype(numpy.float64).astype(numpy.float32)
equal = (rnd32b == rnd32).sum()
equal
100000000
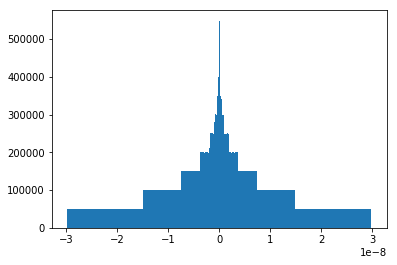
Let’s study the distribution of the difference.
delta = rnd - rnd32
numpy.min(delta), numpy.max(delta)
(-2.9802321610539195e-08, 2.9802320611338473e-08)
numpy.min(rnd), numpy.max(rnd)
(5.400330183036317e-10, 0.9999999976946683)
import matplotlib.pyplot as plt
plt.hist(delta, bins=1000);
We finally check that double operations between float numpers remain floats.
import random
for i in range(0,100000):
i,j = random.randint(0, len(rnd32)-1), random.randint(0, len(rnd32)-1)
d32 = numpy.float64(rnd32[i] * rnd32[j])
d64 = numpy.float64(rnd32[i]) * numpy.float64(rnd32[j])
if d32 != d64:
raise Exception("Issue with somme={0} = {1} + {2}".format(rnd32[i] + rnd32[j], rnd32[i], rnd32[j]))
Interval length distribution#
Let’s imagine now we want to define an intervalle in which a double is converted to the same float. Let’s find out about it length.
def find_interval(x):
dx = numpy.abs(x - numpy.float32(x)) # usually not zero
dx /= 100
f = numpy.float32(x)
x1 = x
while numpy.float32(x1) == f:
x1 -= dx
x2 = x
while numpy.float32(x2) == f:
x2 += dx
return x1 + dx, x2 - dx
length = numpy.zeros((2000,))
for i in range(length.shape[0]):
x = rnd[i]
x1, x2 = find_interval(x)
length[i] = x2-x1
min(length), max(length)
(7.245554200022153e-12, 5.9604641222676946e-08)
plt.hist(length, bins=50);
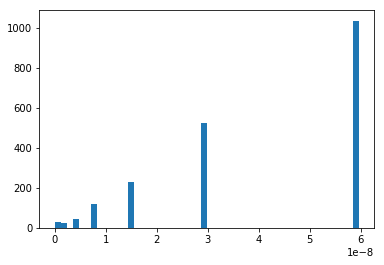
So we can approximate this interval by something like this:
ql = numpy.sort(length)[int(length.shape[0] * 0.8)]
ql
5.953141313241872e-08
An answer to the initial question#
Let’s estimate
?
import pandas
def inf_strict(x, y):
f1 = x < y
f2 = numpy.float32(x) < numpy.float32(y)
return f1, f2
def count_events(fct):
rows = []
for di in range(1, 1001):
d = di * ql / 100
total = 0
ok = 0
rnd = numpy.random.random((2000*3,))
for i in range(0, rnd.shape[0], 3):
s = -1 if rnd[i+2] < 0.5 else 1
x, y = rnd[i], rnd[i] + rnd[i+1]*d*s
f1, f2 = fct(x, y)
if f1:
total += 1
if f2:
ok += 1
if (di+10) % 100 == 0:
print(di, d, ":", ok, total)
rows.append(dict(d=d, ratio=ok*1./total, total=total))
return pandas.DataFrame(rows)
df = count_events(inf_strict)
df.head()
90 5.357827181917685e-08 : 638 991
190 1.1310968495159557e-07 : 812 1018
290 1.726410980840143e-07 : 889 1011
390 2.32172511216433e-07 : 918 986
490 2.9170392434885173e-07 : 901 981
590 3.5123533748127045e-07 : 936 986
690 4.1076675061368917e-07 : 964 1004
790 4.702981637461079e-07 : 982 1021
890 5.298295768785266e-07 : 964 998
990 5.893609900109453e-07 : 946 975
| d | ratio | total | |
|---|---|---|---|
| 0 | 5.953141e-10 | 0.019447 | 977 |
| 1 | 1.190628e-09 | 0.041879 | 979 |
| 2 | 1.785942e-09 | 0.065590 | 991 |
| 3 | 2.381257e-09 | 0.063000 | 1000 |
| 4 | 2.976571e-09 | 0.072217 | 997 |
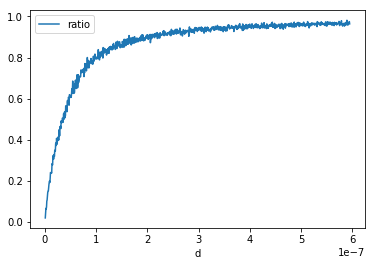
df.plot(x="d", y="ratio")
<matplotlib.axes._subplots.AxesSubplot at 0x20e376592e8>
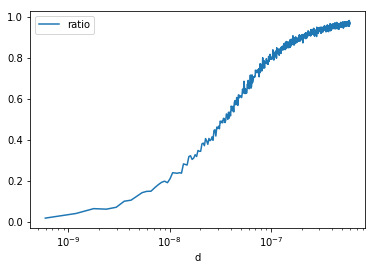
df.plot(x="d", y="ratio", logx=True)
<matplotlib.axes._subplots.AxesSubplot at 0x20e37aa48d0>
An answer to a similar question: what about not strict comparison?#
Let’s estimate
?
def inf_equal(x, y):
f1 = x <= y
f2 = numpy.float32(x) <= numpy.float32(y)
return f1, f2
df2 = count_events(inf_equal)
df2.head()
90 5.357827181917685e-08 : 966 966
190 1.1310968495159557e-07 : 1015 1015
290 1.726410980840143e-07 : 1004 1004
390 2.32172511216433e-07 : 991 991
490 2.9170392434885173e-07 : 1015 1015
590 3.5123533748127045e-07 : 975 975
690 4.1076675061368917e-07 : 969 969
790 4.702981637461079e-07 : 962 962
890 5.298295768785266e-07 : 1032 1032
990 5.893609900109453e-07 : 1000 1000
| d | ratio | total | |
|---|---|---|---|
| 0 | 5.953141e-10 | 1.0 | 996 |
| 1 | 1.190628e-09 | 1.0 | 969 |
| 2 | 1.785942e-09 | 1.0 | 1004 |
| 3 | 2.381257e-09 | 1.0 | 979 |
| 4 | 2.976571e-09 | 1.0 | 1041 |
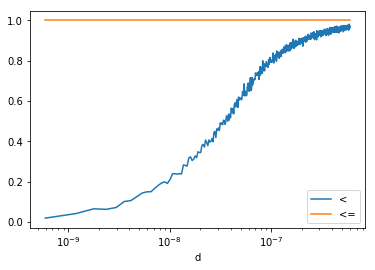
ax = df.plot(x="d", y="ratio", logx=True, label="<")
df2.plot(x="d", y="ratio", logx=True, label="<=", ax=ax)
<matplotlib.axes._subplots.AxesSubplot at 0x20e37aec400>
def sup_strict(x, y):
f1 = x > y
f2 = numpy.float32(x) > numpy.float32(y)
return f1, f2
df3 = count_events(sup_strict)
df3.head()
90 5.357827181917685e-08 : 652 1008
190 1.1310968495159557e-07 : 799 964
290 1.726410980840143e-07 : 871 994
390 2.32172511216433e-07 : 881 969
490 2.9170392434885173e-07 : 961 1014
590 3.5123533748127045e-07 : 906 958
690 4.1076675061368917e-07 : 930 973
790 4.702981637461079e-07 : 1004 1036
890 5.298295768785266e-07 : 962 1012
990 5.893609900109453e-07 : 972 1016
| d | ratio | total | |
|---|---|---|---|
| 0 | 5.953141e-10 | 0.024291 | 988 |
| 1 | 1.190628e-09 | 0.044838 | 959 |
| 2 | 1.785942e-09 | 0.057769 | 1004 |
| 3 | 2.381257e-09 | 0.087000 | 1000 |
| 4 | 2.976571e-09 | 0.091769 | 1057 |
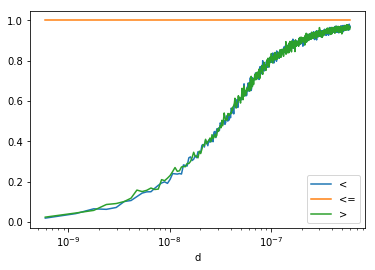
ax = df.plot(x="d", y="ratio", logx=True, label="<")
df2.plot(x="d", y="ratio", logx=True, label="<=", ax=ax)
df3.plot(x="d", y="ratio", logx=True, label=">", ax=ax)
<matplotlib.axes._subplots.AxesSubplot at 0x20e37b94da0>
def sup_equal(x, y):
f1 = x >= y
f2 = numpy.float32(x) >= numpy.float32(y)
return f1, f2
df4 = count_events(sup_equal)
df4.head()
90 5.357827181917685e-08 : 964 964
190 1.1310968495159557e-07 : 1010 1010
290 1.726410980840143e-07 : 1009 1009
390 2.32172511216433e-07 : 990 990
490 2.9170392434885173e-07 : 967 967
590 3.5123533748127045e-07 : 1019 1019
690 4.1076675061368917e-07 : 1013 1013
790 4.702981637461079e-07 : 1020 1020
890 5.298295768785266e-07 : 996 996
990 5.893609900109453e-07 : 964 964
| d | ratio | total | |
|---|---|---|---|
| 0 | 5.953141e-10 | 1.0 | 1031 |
| 1 | 1.190628e-09 | 1.0 | 1013 |
| 2 | 1.785942e-09 | 1.0 | 975 |
| 3 | 2.381257e-09 | 1.0 | 998 |
| 4 | 2.976571e-09 | 1.0 | 1022 |
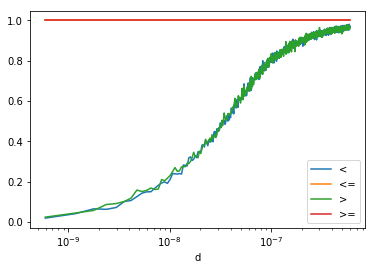
ax = df.plot(x="d", y="ratio", logx=True, label="<")
df2.plot(x="d", y="ratio", logx=True, label="<=", ax=ax)
df3.plot(x="d", y="ratio", logx=True, label=">", ax=ax)
df4.plot(x="d", y="ratio", logx=True, label=">=", ax=ax)
<matplotlib.axes._subplots.AxesSubplot at 0x20e38d39e48>
def inf_strict_neg(x, y):
f1 = (-x) >= (-y)
f2 = (-numpy.float32(x)) >= (-numpy.float32(y))
return f1, f2
dfn = count_events(inf_strict_neg)
dfn.head()
90 5.357827181917685e-08 : 999 999
190 1.1310968495159557e-07 : 1019 1019
290 1.726410980840143e-07 : 1013 1013
390 2.32172511216433e-07 : 994 994
490 2.9170392434885173e-07 : 1012 1012
590 3.5123533748127045e-07 : 984 984
690 4.1076675061368917e-07 : 1024 1024
790 4.702981637461079e-07 : 982 982
890 5.298295768785266e-07 : 966 966
990 5.893609900109453e-07 : 1001 1001
| d | ratio | total | |
|---|---|---|---|
| 0 | 5.953141e-10 | 1.0 | 976 |
| 1 | 1.190628e-09 | 1.0 | 983 |
| 2 | 1.785942e-09 | 1.0 | 1024 |
| 3 | 2.381257e-09 | 1.0 | 966 |
| 4 | 2.976571e-09 | 1.0 | 1016 |
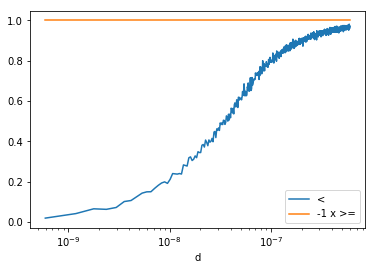
ax = df.plot(x="d", y="ratio", logx=True, label="<")
dfn.plot(x="d", y="ratio", logx=True, label="-1 x >=", ax=ax)
<matplotlib.axes._subplots.AxesSubplot at 0x20e391d8eb8>
Conclusion#
The result is expected. As soon as two float are rounded to the same
value, the strict inequality no longer holds. However, if you need to
write a code which has to handle double and float (in a template for
example), you should use not strict inequalities. It is easier to
compare the results but you should read some article like Is < faster
than
<=?.
According to Processing costs of non-strict versus strict
comparison, < is
5-10% faster than <=.