2013-02-07 How to extend a stack?
A common way to create a sizeable but continuous array is to use a stack mechanism. We start by allocating a buffer and when we need more space to store new elements, we often multiply the size of this buffer by 2. We copy the existing elements into the new space, we add the new one and we free the old buffer. If we follow that strategy for a long time, we end up by allocation memory blocks of size N, 2N, 4N, 8N, ... The major drawback of this approach is we cannot reuse the space we used for the first allocation. The reason is simple:
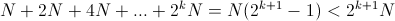
As a consequence, the new buffer is always larger than the sum of all previously allocated block. And we because, we need to keep the last one alive to copy the existing elements to the new block, this way of growing a stack cannot reuse the same memory space. This side effect could increase the memory fragmentation.
What does happen if we multiply the size of a block by a coefficient c smaller than 2:
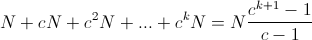
We need to compare that sum to:
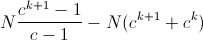
We can remove N from the equation:
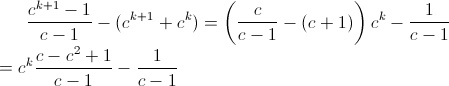
This expression is positive if and only if:
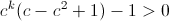
So first, we must have 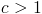 .
Second, we must also have
.
Second, we must also have 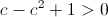 , which means:
, which means:
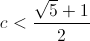
If that condition is fulfilled then, there will k for which the above expression becomes positive.
Now, we can think about the number of copies we made to reach a given size S of stack. Assuming c is fixed, we need to find k such as:
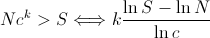
Once we determine k, we can compute the number of times we copied an element from an old buffer to a new one. Obviously, the first element was copied k times, elements after position N were copied at most k-1times. Elements after position N + c N were copied at most k-2 times. The number of copies becomes:
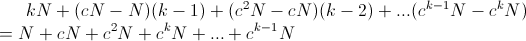
Finally, the number of copies is:
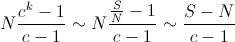
So we should choose c as big as possible and strictly
inferior to 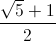 .
.