2013-11-09 Compter les pièces de monnaie pour obtenir un montant
On est amené presque tous les jours à compter les pièces dans son porte-monnaie pour payer la baguette, le fromage ou la bouteille de vin. Comment écrire un algorithme qui donne la liste des pièces qu'il faut piocher dans son porte-monnaie pour payer ? On s'intéressera seulement au cas où on cherche à composer le montant juste. Cela revient à chercher un sous-ensemble S de pièces dans l'ensemble P des pièces du portefeuille pour composer le montant M :
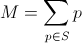
Une façon naïve de construire l'ensemble S est de procéder comme on le fait souvent, c'est-à-dire à prendre la pièce la plus grosse, de voir si elle dépasse le montant N puis de passer à la seconde plus grande et ainsi de suite. Soit :
- On trie les pièces par ordre décroissant.
- Au début, l'ensembe S est vide.
- On prend les pièces dans l'ordre décroissant et on les ajoute à l'ensemble S si la somme de l'ensemble n'est pas plus grand que M.
def composition_montant(M, P) :
P.sort(reverse=True)
S = [ ]
for p in P :
if sum(S) + p <= M :
S.append(p)
return S
print ( composition_montant ( 13, [ 1,10,5,2] ) ) # affiche [10, 2, 1]
Mais l'algorithme n'est pas parfait. Par exemple, il n'arrive pas à trouver la bonne solution pour M=6 et P =[ 5,2,2,2] :
print ( composition_montant ( 6, [ 5,2,2,2] ) ) # affiche [ 5 ]
L'algorithme choisit la première pièce car elle est inférieure au montant mais se retrouve coincé par la suite car toutes les pièces qu'il ajoute lui font dépasser le montant. On peut dans un premier lui permettre de "sauter" la première pièce :
# coding: latin-1
def composition_montant(M, P) :
P.sort(reverse=True)
S = [ ]
for p in P :
if sum(S) + p <= M :
S.append(p)
return S
def composition_premiere_piece_en_moins(M, P) :
r = composition_montant(M,P)
if sum(r) != M :
r = composition_montant(M,P[1:])
return r
print ( composition_premiere_piece_en_moins ( 13, [ 1,10,5,2] )) # affiche [ 10,2,1 ]
print ( composition_premiere_piece_en_moins ( 6, [ 5,2,2,2] )) # affiche [ 2,2,2 ]
print ( composition_premiere_piece_en_moins ( 106, [ 100,5,2,2,2] )) # affiche [ 5,2,2,2 ]
Là encore, ça marche pour les deux premiers exemples mais pas pour le troisième suggéré ci-dessus. Une solution est de pouvoir "sauter" la première pièce mais aussi les suivantes :
# coding: latin-1
def composition_montant(M, P) :
#P.sort(reverse=True) # on déplace cette ligne là où elle ne sera executée qu'une fois
S = [ ]
for p in P :
if sum(S) + p <= M :
S.append(p)
return S
def composition_une_piece_en_moins(M, P) :
P.sort(reverse=True) # on trie ici pour ne le faire qu'une seule fois
r = composition_montant(M,P)
if sum(r) != M :
for i,p in enumerate(P) :
if p <= M : # les pièces plus grandes que M ne sont pas prises en compte
P[i] = M+1 # on remplace la valeur de la pièce par M+1, de cette manière
# elle ne sera pas choisie pour composer le montant M
# on appelle la fonction précédente
r2 = composition_montant(M,P)
if sum(r2) == M :
# si ça marche, on a fini
return r2
P[i] = p # on remet P en place
return r
print ( composition_une_piece_en_moins ( 13, [ 1,10,5,2] )) # affiche [ 10,2,1 ]
print ( composition_une_piece_en_moins ( 6, [ 5,2,2,2] )) # affiche [ 2,2,2 ]
print ( composition_une_piece_en_moins ( 106, [ 100,5,2,2,2] )) # affiche [ 100,2,2,2 ]
print ( composition_une_piece_en_moins ( 6, [ 5,5,2,2,2] )) # affiche [ 5 ]
On avance mais cela ne fonctionne toujours pas pour le dernier exemple. Il faudrait pouvoir sauter plusieurs pièces. Et c'est en fait très simple à faire, il suffit de rendre la fonction composition_une_piece_en_moins récursive :
# coding: latin-1
def composition_montant(M, P) :
P.sort(reverse=True)
S = [ ]
for p in P :
if sum(S) + p <= M :
S.append(p)
return S
def composition_une_piece_en_moins(M, P) :
P.sort(reverse=True)
r = composition_montant(M,P)
if sum(r) != M :
for i,p in enumerate(P) :
if p <= M :
P[i] = M+1
# il faut utiliser P.copy() et non P
# sauf si on retire l'instruction P.sort car celle-ci change l'ordre
# des éléments (il est donc difficile de remettre la pièce en place à la fin de la boucle
r2 = composition_une_piece_en_moins(M,P.copy())
if sum(r2) == M :
return r2
P[i] = p
return r
print ( composition_une_piece_en_moins ( 13, [ 1,10,5,2] )) # affiche [ 10,2,1 ]
print ( composition_une_piece_en_moins ( 6, [ 5,2,2,2] )) # affiche [ 2,2,2 ]
print ( composition_une_piece_en_moins ( 106, [ 100,5,2,2,2] )) # affiche [ 100,2,2,2 ]
print ( composition_une_piece_en_moins ( 6, [ 5,5,2,2,2] )) # affiche [ 2,2,2 ]
Qu'a-t-on fait ? Une première façon de voir les choses est de se dire qu'une pièce appartient ou non à l'ensemble S. Donc si, le portefeuille contient N pièces, il y a 2^N façons de construire l'ensemble S. Et c'est ce que fait la fonction composition_une_piece_en_moins : elle essaye d'abord avec toutes les pièces. Puis, si ça ne marche pas, elle enlève une pièce et réessaye en se rappelant. Comme elle se rappelle elle-même, il lui est possible maintenant d'enlever une seconde pièce, puis une autre à chaque récurrence jusqu'à ce qu'il n'en reste plus. De cette façon, la fonction aura essayé toutes les compositions possibles des pièces du portefeuille pour s'arrêter à la première qui marche. Pour faire court, on parcourt les 2^N possibilités, ce qu'il était sans doute plus simple d'écrire comme ceci :
def composition_plus_simple(M,P) :
r = sum(P)
if r == M : return P
for i in range(0,len(P)) :
r = composition_plus_simple (M, P[:i] + P[i+1:])
if r != None : return r
return None # pas de solution
print ( composition_plus_simple ( 13, [ 1,10,5,2] )) # affiche [ 10,2,1 ]
print ( composition_plus_simple ( 6, [ 5,2,2,2] )) # affiche [ 2,2,2 ]
print ( composition_plus_simple ( 106, [ 100,5,2,2,2] )) # affiche [ 100,2,2,2 ]
print ( composition_plus_simple ( 6, [ 5,5,2,2,2] )) # affiche [ 2,2,2 ]
Pour être exact, la fonction précédente (comme celle d'avant), parcourt toutes les solutions en tenant compte de l'ordre : elle pourra supprimer la pièce 1 puis la pièce 2 tout comme elle supprimera la pièces 2 puis la pièce 1. Or pour notre problème, ça ne change rien. Donc, on pourrait faire encore plus simple puisque cette fois-ci, on n'explore pas deux fois la même solution :
# coding: latin-1
def composition_plus_simple(M,P) :
if len(P) == 0 : return [ ]
if sum(P) == M : return P
r = composition_plus_simple(M,P[1:]) # on enlève la pièce
if sum(r) == M : return r
r = [ P[0] ] + composition_plus_simple(M-P[0],P[1:])
# on garde la pièce mais on cherche à obtenir la différence avec les pièces restantes
if sum(r) == M : return r
else : return []
print ( composition_plus_simple ( 13, [ 1,10,5,2] )) # affiche [ 1,10,2 ]
print ( composition_plus_simple ( 6, [ 5,2,2,2] )) # affiche [ 2,2,2 ]
print ( composition_plus_simple ( 106, [ 100,5,2,2,2] )) # affiche [ 100,2,2,2 ]
print ( composition_plus_simple ( 6, [ 5,5,2,2,2] )) # affiche [ 2,2,2 ]
Existe-t-il un algorithme plus rapide ? La réponse est oui : il existe un algorithme de coût quadratique. Ce problème n'est pas très éloigné du problème du sac-à-dos pour lequel il existe une solution quadratique dans le cas où les objets à ranger dans le sac sont de poids entier. Ca tombe bien, c'est notre cas ici (pièces en euros ou en cents). L'algorithme a pour coût O(NM) où N est le nombre de pièces et M le montant. Dans un premier temps, on va écrire une fonction qui détermine si un montant pour être composé à partir d'un ensemble de pièces. L'idée de base de l'algorithme est :
On en déduit l'algorithme suivant :
- Au début on dispose d'un tableau tab de dimension M+1, initialisé à 0. Si ce tableau contient une valeur non nulle d'indice m, alors cette valeur correspond au nombre de pièces utilisées pour composer le montant m.
- Pour chaque pièce p, on parcourt tous les montants m en sens inverse :
- si tab[m-p] est non nul alors on peut écrire le montant m avec la pièce p en plus
- si m==p, on peut évidemment écrire le montant m.
- à la fin, si tab[M] est non nul, alors on peut composer le montant M.
def composition_possible_dynamique(M, P) :
tab = [ 0 for i in range(M+1) ]
for p in P :
for m in range(M,0,-1) :
if m-p >= 0 and (m == p or tab[m-p] > 0) :
if tab[m] == 0 :
tab[m] = tab[m-p] + 1
else :
tab[m] = min(tab[m],tab[m-p] + 1)
return tab[M]
print ( composition_possible_dynamique ( 13, [ 1,10,10,5,2] )) # affiche 3
print ( composition_possible_dynamique ( 6, [ 5,2,2,2] )) # affiche 3
print ( composition_possible_dynamique ( 106, [ 100,5,2,2,2] )) # affiche 4
print ( composition_possible_dynamique ( 6, [ 5,5,2,2,2] )) # affiche 3
print ( composition_possible_dynamique ( 6, [ 5,5,2,3,2] )) # affiche 0
L'instruction range(M,0,-1) permet de parcourir les montant en sens inverse ce qui nous assure qu'une pièce n'est utilisée qu'une seule fois. En effet, si on parcourt les montants dans le sens croissant, le tableau tab contiendra des valeurs possibles pour tous les multiples de la pièce p (je vous laisse comprendre pourquoi).
Autre remarque : l'ordre des pièces importe peu. D'ailleurs, l'algorithme fonctionne justement parce que la solution ne dépend pas de l'ordre des pièces.
Et pour obtenir cette solution, il ne reste plus qu'à récupérer la liste des pièces. On conserve, dans un second tableau prec, la dernière pièce qui a permis d'obtenir le nombre minimal de pièces pour composer le montant m.
def composition_dynamique(M, P) :
tab = [ 0 for i in range(M+1) ]
prec = [ 0 for i in range(M+1) ]
for p in P :
for m in range(M,0,-1) :
if m-p >= 0 and (m == p or tab[m-p] > 0) :
if tab[m] == 0 :
tab[m] = tab[m-p] + 1
prec[m] = p
elif tab[m] > tab[m-p] + 1 :
tab[m] = tab[m-p] + 1
prec[m] = p
if tab[M] > 0 :
piece = [ ]
pos = M
while pos > 0 :
piece.append(prec[pos])
pos -= prec[pos]
return piece
else :
return []
print ( composition_dynamique ( 13, [ 1,10,10,5,2] )) # affiche [ 2,10,1 ]
print ( composition_dynamique ( 6, [ 5,2,2,2] )) # affiche [ 2,2,2 ]
print ( composition_dynamique ( 106, [ 100,5,2,2,2] )) # affiche [ 2,2,2,100 ]
print ( composition_dynamique ( 6, [ 5,5,2,2,2] )) # affiche [ 2,2,2 ]
print ( composition_dynamique ( 6, [ 5,5,2,3,2] )) # affiche [ ]
On peut comparer les temps de traitement de deux solutions, une d'un coût quadratique et l'autre d'un coût exponentiel :
import random, time
exemples = []
N = 21
for i in range (0,1000) :
l = random.randint(1,N) #
M = random.randint(1,100)
P = [ random.randint(1,20) for i in range(l) ]
exemples.append((M,P))
temps_exp = time.clock()
for M,P in exemples :
composition_plus_simple(M,P)
temps_exp = time.clock() - temps_exp
print (temps_exp)
temps_dyn = time.clock()
for M,P in exemples :
composition_dynamique(M,P)
temps_dyn = time.clock() - temps_dyn
print (temps_exp, temps_dyn) # 5.945673611467473 0.24070277620978064
Le temps exponentiel double à chaque qu'on augmente N de 1.