2A.ml - Interprétabilité et corrélations des variables#
Links: notebook, html, python, slides, GitHub
Plus un modèle de machine learning contient de coefficients, moins sa décision peut être interprétée. Comment contourner cet obstacle et comprendre ce que le modèle a appris ? Notion de feature importance.
from jyquickhelper import add_notebook_menu
add_notebook_menu()
# Répare une incompatibilité entre scipy 1.0 et statsmodels 0.8.
from pymyinstall.fix import fix_scipy10_for_statsmodels08
fix_scipy10_for_statsmodels08()
Modèles linéaires#
Les modèles linéaires sont les modèles les plus simples à interpréter. A performance équivalente, il faut toujours choisir le modèle le plus simple. Le module scikit-learn ne propose pas les outils standards d’analyse des modèles linéaires (test de nullité, valeur propre). Il faut choisir statsmodels pour obtenir ces informations.
import numpy
import statsmodels.api as smapi
nsample = 100
x = numpy.linspace(0, 10, 100)
X = numpy.column_stack((x, x**2 - x))
beta = numpy.array([1, 0.1, 10])
e = numpy.random.normal(size=nsample)
X = smapi.add_constant(X)
y = X @ beta + e
C:Python395_x64libsite-packagesstatsmodelstsabasetsa_model.py:7: FutureWarning: pandas.Int64Index is deprecated and will be removed from pandas in a future version. Use pandas.Index with the appropriate dtype instead. from pandas import (to_datetime, Int64Index, DatetimeIndex, Period, C:Python395_x64libsite-packagesstatsmodelstsabasetsa_model.py:7: FutureWarning: pandas.Float64Index is deprecated and will be removed from pandas in a future version. Use pandas.Index with the appropriate dtype instead. from pandas import (to_datetime, Int64Index, DatetimeIndex, Period,
model = smapi.OLS(y, X)
results = model.fit()
results.summary()
| Dep. Variable: | y | R-squared: | 1.000 |
|---|---|---|---|
| Model: | OLS | Adj. R-squared: | 1.000 |
| Method: | Least Squares | F-statistic: | 3.222e+06 |
| Date: | Sat, 12 Feb 2022 | Prob (F-statistic): | 1.30e-234 |
| Time: | 18:53:30 | Log-Likelihood: | -147.79 |
| No. Observations: | 100 | AIC: | 301.6 |
| Df Residuals: | 97 | BIC: | 309.4 |
| Df Model: | 2 | ||
| Covariance Type: | nonrobust |
| coef | std err | t | P>|t| | [0.025 | 0.975] | |
|---|---|---|---|---|---|---|
| const | 1.2570 | 0.317 | 3.969 | 0.000 | 0.628 | 1.886 |
| x1 | 0.0134 | 0.133 | 0.101 | 0.920 | -0.250 | 0.277 |
| x2 | 10.0052 | 0.014 | 706.336 | 0.000 | 9.977 | 10.033 |
| Omnibus: | 4.968 | Durbin-Watson: | 1.920 |
|---|---|---|---|
| Prob(Omnibus): | 0.083 | Jarque-Bera (JB): | 2.455 |
| Skew: | -0.037 | Prob(JB): | 0.293 |
| Kurtosis: | 2.236 | Cond. No. | 125. |
Notes:
[1] Standard Errors assume that the covariance matrix of the errors is correctly specified.
Arbres (tree)#
Lectures#
Making Tree Ensembles Interpretable : l’article propose de simplifier une random forest en approximant sa sortie par une somme pondérée d’arbre plus simples.
Understanding variable importances in forests of randomized trees : cet article explique plus formellement le calcul des termes
feature_importances_calculés par scikit-learn pour chaque arbre et forêts d’arbres (voir aussi Random Forests, Leo Breiman and Adele Cutler)
Module treeinterpreter#
from sklearn.datasets import load_iris
iris = load_iris()
X = iris.data
Y = iris.target
from sklearn.tree import DecisionTreeClassifier
clf2 = DecisionTreeClassifier(max_depth=3)
clf2.fit(X, Y)
Yp2 = clf2.predict(X)
from sklearn.tree import export_graphviz
export_graphviz(clf2, out_file="arbre.dot")
import os
cwd = os.getcwd()
from pyquickhelper.helpgen import find_graphviz_dot
dot = find_graphviz_dot()
os.system ("\"{1}\" -Tpng {0}\\arbre.dot -o {0}\\arbre.png".format(cwd, dot))
0
from IPython.display import Image
Image("arbre.png")
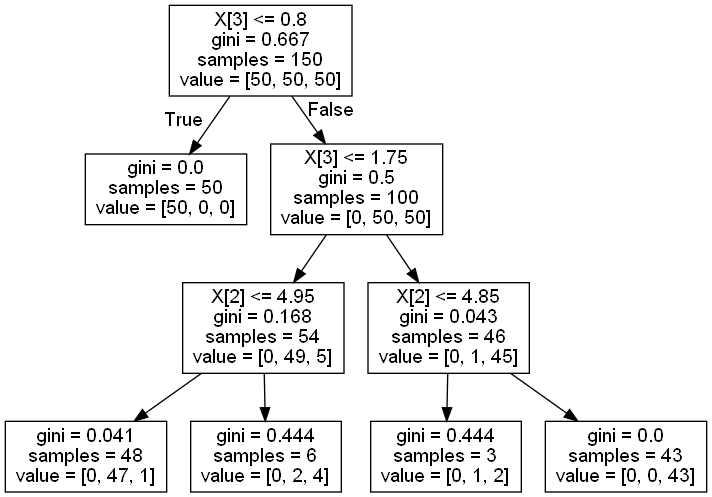
from treeinterpreter import treeinterpreter
pred, bias, contrib = treeinterpreter.predict(clf2, X[106:107,:])
X[106:107,:]
array([[4.9, 2.5, 4.5, 1.7]])
pred
array([[0. , 0.97916667, 0.02083333]])
bias
array([[0.33333333, 0.33333333, 0.33333333]])
contrib
array([[[ 0. , 0. , 0. ],
[ 0. , 0. , 0. ],
[ 0. , 0.07175926, -0.07175926],
[-0.33333333, 0.57407407, -0.24074074]]])
pred est identique à ce que retourne la méthode predict de
scikit-learn. bias est la proportion de chaque classe. contrib
est la somme des contributions de chaque variable à chaque classe. On
note une observation.
Le
code
est assez facile à lire et permet de comprendre ce que vaut la fonction
.
Exercice 1 : décrire la fonction contrib#
La lecture de Understanding variable importances in forests of randomized trees devrait vous y aider.
clf2.feature_importances_
array([0. , 0. , 0.05393633, 0.94606367])
Exercice 2 : implémenter l’algorithme#
Décrit dans Making Tree Ensembles Interpretable
Interprétation et corrélation#
Modèles linéaires#
Les modèles linéaires n’aiment pas les variables corrélées. Dans
l’exemple qui suit, les variables sont identiques. La
régression ne peut retrouver les coefficients du modèle initial (2 et
8).
import numpy
import statsmodels.api as smapi
nsample = 100
x = numpy.linspace(0, 10, 100)
X = numpy.column_stack((x, (x-5)**2, (x-5)**2)) # ajout de la même variable
beta = numpy.array([1, 0.1, 2, 8])
e = numpy.random.normal(size=nsample)
X = smapi.add_constant(X)
y = X @ beta + e
import pandas
pandas.DataFrame(numpy.corrcoef(X.T))
C:Python395_x64libsite-packagesnumpylibfunction_base.py:2691: RuntimeWarning: invalid value encountered in true_divide c /= stddev[:, None] C:Python395_x64libsite-packagesnumpylibfunction_base.py:2692: RuntimeWarning: invalid value encountered in true_divide c /= stddev[None, :]
| 0 | 1 | 2 | 3 | |
|---|---|---|---|---|
| 0 | NaN | NaN | NaN | NaN |
| 1 | NaN | 1.000000e+00 | 8.513703e-17 | 8.513703e-17 |
| 2 | NaN | 8.513703e-17 | 1.000000e+00 | 1.000000e+00 |
| 3 | NaN | 8.513703e-17 | 1.000000e+00 | 1.000000e+00 |
model = smapi.OLS(y, X)
results = model.fit()
results.summary()
| Dep. Variable: | y | R-squared: | 1.000 |
|---|---|---|---|
| Model: | OLS | Adj. R-squared: | 1.000 |
| Method: | Least Squares | F-statistic: | 3.806e+05 |
| Date: | Sat, 12 Feb 2022 | Prob (F-statistic): | 1.27e-189 |
| Time: | 18:53:59 | Log-Likelihood: | -126.59 |
| No. Observations: | 100 | AIC: | 259.2 |
| Df Residuals: | 97 | BIC: | 267.0 |
| Df Model: | 2 | ||
| Covariance Type: | nonrobust |
| coef | std err | t | P>|t| | [0.025 | 0.975] | |
|---|---|---|---|---|---|---|
| const | 0.5470 | 0.199 | 2.756 | 0.007 | 0.153 | 0.941 |
| x1 | 0.1396 | 0.030 | 4.671 | 0.000 | 0.080 | 0.199 |
| x2 | 4.9989 | 0.006 | 872.449 | 0.000 | 4.988 | 5.010 |
| x3 | 4.9989 | 0.006 | 872.449 | 0.000 | 4.988 | 5.010 |
| Omnibus: | 2.677 | Durbin-Watson: | 2.150 |
|---|---|---|---|
| Prob(Omnibus): | 0.262 | Jarque-Bera (JB): | 1.871 |
| Skew: | 0.133 | Prob(JB): | 0.392 |
| Kurtosis: | 2.385 | Cond. No. | 1.41e+16 |
Notes:
[1] Standard Errors assume that the covariance matrix of the errors is correctly specified.
[2] The smallest eigenvalue is 1.39e-28. This might indicate that there are
strong multicollinearity problems or that the design matrix is singular.
Arbre / tree#
Les arbres de décision n’aiment pas plus les variables corrélées.
from sklearn.datasets import load_iris
iris = load_iris()
X = iris.data[:,:2]
Y = iris.target
from sklearn.tree import DecisionTreeClassifier
clf1 = DecisionTreeClassifier(max_depth=3)
clf1.fit(X, Y)
DecisionTreeClassifier(max_depth=3)
clf1.feature_importances_
array([0.76759205, 0.23240795])
On recopie la variables .
import numpy
X2 = numpy.hstack([X, numpy.ones((X.shape[0], 1))])
X2[:,2] = X2[:,0]
clf2 = DecisionTreeClassifier(max_depth=3)
clf2.fit(X2, Y)
DecisionTreeClassifier(max_depth=3)
clf2.feature_importances_
array([0.14454858, 0.23240795, 0.62304347])
On voit que l’importance de la variable 1 est diluée sur deux variables.
Exercice 3 : variables corrélées pour un arbre de décision#
Un arbre de décision est composé d’un ensemble de fonctions de seuil. Si
alors il faut suivre cette branche, sinon, telle
autre. Les arbres de décision ne sont pas sensibles aux problèmes
d’échelle de variables. Si deux variables sont corrélées
, l’arbre subit les mêmes problèmes qu’un modèle
linéaire. Dans le cas linéaire, il suffit de changer l’échelle
pour éviter ce problème.
Pourquoi cette transformation ne change rien pour un arbre de décision ?
Quelle corrélation il faudrait calculer pour repérer les variables identiques selon le point de vue d’un arbre de décision ?