2A.ml - Séries temporelles#
Links: notebook, html, python, slides, GitHub
Prédictions sur des séries temporelles et autres opérations classiques.
from jyquickhelper import add_notebook_menu
add_notebook_menu()
%matplotlib inline
Une série temporelle#
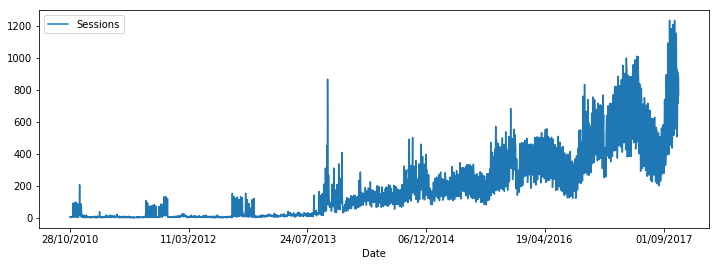
On récupère le nombre de sessions d’un site web : xavierdupre_sessions.csv.
import pyensae.datasource as ds
ds.download_data('xavierdupre_sessions.csv',
url='https://raw.githubusercontent.com/sdpython/ensae_teaching_cs/master/_doc/notebooks/td2a_ml/')
'xavierdupre_sessions.csv'
import pandas
data = pandas.read_csv("xavierdupre_sessions.csv", sep="\t")
data.set_index("Date", inplace=True)
data.plot(figsize=(12,4))
<matplotlib.axes._subplots.AxesSubplot at 0x2bb8d742128>
data[-365:].plot(figsize=(12,4))
<matplotlib.axes._subplots.AxesSubplot at 0x2bb8dba3208>
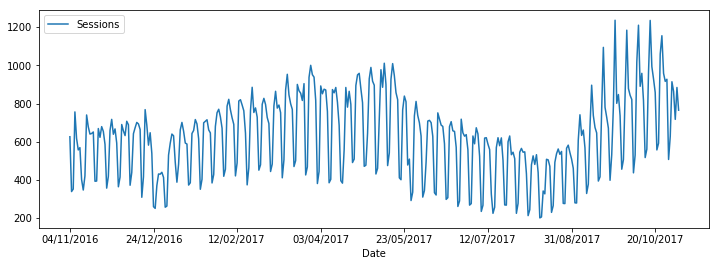
Exercice 1 : tendance#
Fonction detrend. Enlever la tendance.
from statsmodels.tsa.tsatools import detrend
Exercice 2 : enlever la saisonnalité#
Avec deux fonctions seasonal_decompose ou fit_seasons
from statsmodels.tsa.seasonal import seasonal_decompose
from seasonal import fit_seasons
Exercice 3 : Auto-corrélograme, périodogramme#
On s’inspire de l’exemple : Autoregressive Moving Average (ARMA): Sunspots data.
import matplotlib.pyplot as plt
from statsmodels.graphics.tsaplots import plot_acf, plot_pacf
c:python36_x64libsite-packagesstatsmodelscompatpandas.py:56: FutureWarning: The pandas.core.datetools module is deprecated and will be removed in a future version. Please use the pandas.tseries module instead. from pandas.core import datetools
Exercice 4 : caler un modèle à changement de régime#
Exercice 5 : calculer la série décalée#
Voir méthode shift.
Exercice 6 : calculer la performance de prédiction de la veille pour le lendemain#
C’est la prédiction la plus simple mais toute performance en deça du chiffre obtenue veut tout simplement dire que le modèle prédictif évalué ne prédit pas mieux que la valeur de la veille.
Exercice 7 : caler une régression linéaire#
On note . Estimer un modèle
. Garder les quatre derniers
mois comme base de test.
Exercice 8 : remplacer la random forest par un arbre de décision#
Quel est le meilleur modèle ?