Examples#
Change ONNX model inputs
The following exampels shows how to change the inputs of model to bypass the first nodes. Shape inferences fails to determine the new inputs type. They need to be overwritten. verbose=1, fLOG=print shows the number of deleted nodes.
import onnx
from mlprodict.onnx_tools.onnx_manipulations import select_model_inputs_outputs
onx = onnx.load(path)
onx2 = select_model_inputs_outputs(
onx, inputs=["SentenceTokenizer/SentencepieceTokenizeOp:0",
"SentenceTokenizer/SentencepieceTokenizeOp:1"],
infer_shapes=True, verbose=1, fLOG=print,
overwrite={'SentenceTokenizer/SentencepieceTokenizeOp:0': (numpy.int32, None),
'SentenceTokenizer/SentencepieceTokenizeOp:1': (numpy.int64, None)})
onnx.save(onx2, path2)
(original entry : onnx_manipulations.py:docstring of mlprodict.onnx_tools.onnx_manipulations.select_model_inputs_outputs, line 17)
Computes predictions with any runtime
The following example compares predictions between scikit-learn and this runtime for the python runtime.
<<<
import numpy
from sklearn.linear_model import LinearRegression
from sklearn.datasets import load_iris
from sklearn.model_selection import train_test_split
from mlprodict.onnxrt import OnnxInference
from mlprodict.onnx_conv import to_onnx
iris = load_iris()
X, y = iris.data, iris.target
X_train, X_test, y_train, _ = train_test_split(X, y)
clr = LinearRegression()
clr.fit(X_train, y_train)
exp = clr.predict(X_test[:5])
print(exp)
model_def = to_onnx(clr, X_train.astype(numpy.float32),
target_opset=12)
oinf = OnnxInference(model_def)
y = oinf.run({'X': X_test[:5]})
print(y)
>>>
[0.01 1.365 0.893 0.052 2.04 ]
{'variable': array([[0.01 ],
[1.365],
[0.893],
[0.052],
[2.04 ]])}
(original entry : onnx_inference.py:docstring of mlprodict.onnxrt.onnx_inference.OnnxInference.run, line 23)
Convert ONNX into DOT
An example on how to convert an ONNX graph into DOT.
<<<
import numpy
from mlprodict.npy.xop import loadop
from mlprodict.onnxrt import OnnxInference
OnnxAiOnnxMlLinearRegressor = loadop(
('ai.onnx.ml', 'LinearRegressor'))
pars = dict(coefficients=numpy.array([1., 2.]),
intercepts=numpy.array([1.]),
post_transform='NONE')
onx = OnnxAiOnnxMlLinearRegressor(
'X', output_names=['Y'], **pars)
model_def = onx.to_onnx(
{'X': pars['coefficients'].astype(numpy.float32)},
outputs={'Y': numpy.float32},
target_opset=12)
oinf = OnnxInference(model_def)
print(oinf.to_dot())
>>>
digraph{
size=7;
ranksep=0.25;
nodesep=0.05;
orientation=portrait;
X [shape=box color=red label="X\nfloat((2,))" fontsize=10];
Y [shape=box color=green label="Y\nfloat(('?',))" fontsize=10];
_linearregressor [shape=box style="filled,rounded" color=orange label="LinearRegressor\n(_linearregressor)\ncoefficients=[1. 2.]\nintercepts=[1.]\npost_transform=b'NONE'" fontsize=10];
X -> _linearregressor;
_linearregressor -> Y;
}
See an example of representation in notebook ONNX visualization.
(original entry : onnx_inference_exports.py:docstring of mlprodict.onnxrt.onnx_inference_exports.OnnxInferenceExport.to_dot, line 27)
Convert ONNX into JSON
An example on how to convert an ONNX graph into JSON.
<<<
import numpy
from mlprodict.npy.xop import loadop
from mlprodict.onnxrt import OnnxInference
OnnxAiOnnxMlLinearRegressor = loadop(
('ai.onnx.ml', 'LinearRegressor'))
pars = dict(coefficients=numpy.array([1., 2.]),
intercepts=numpy.array([1.]),
post_transform='NONE')
onx = OnnxAiOnnxMlLinearRegressor(
'X', output_names=['Y'], **pars)
model_def = onx.to_onnx(
{'X': pars['coefficients'].astype(numpy.float32)},
outputs={'Y': numpy.float32},
target_opset=12)
oinf = OnnxInference(model_def)
print(oinf.to_json())
>>>
{
"producer_name": "",
"doc_string": "",
"ir_version": 8,
"producer_version": "",
"model_version": 0,
"domain": "",
"inputs": [
{
"name": "X",
"type": {
"tensor_type": {
"elem_type": 1,
"shape": {
"dim": {
"dim_value": 2
}
}
}
}
}
],
"outputs": [
{
"name": "Y",
"type": {
"tensor_type": {
"elem_type": 1
}
}
}
],
"initializers": {},
"nodes": [
{
"name": "_linearregressor",
"op_type": "LinearRegressor",
"domain": "ai.onnx.ml",
"inputs": [
"X"
],
"outputs": [
"Y"
],
"attributes": {
"coefficients": {
"floats": [
1.0,
2.0
],
"type": "FLOATS"
},
"intercepts": {
"floats": [
1.0
],
"type": "FLOATS"
},
"post_transform": {
"s": "NONE",
"type": "STRING"
}
}
}
]
}
(original entry : onnx_inference_exports.py:docstring of mlprodict.onnxrt.onnx_inference_exports.OnnxInferenceExport.to_json, line 6)
Convert ONNX into graph
An example on how to convert an ONNX graph into a graph.
<<<
import pprint
import numpy
from mlprodict.npy.xop import loadop
from mlprodict.onnxrt import OnnxInference
OnnxAiOnnxMlLinearRegressor = loadop(
('ai.onnx.ml', 'LinearRegressor'))
pars = dict(coefficients=numpy.array([1., 2.]),
intercepts=numpy.array([1.]),
post_transform='NONE')
onx = OnnxAiOnnxMlLinearRegressor(
'X', output_names=['Y'], **pars)
model_def = onx.to_onnx(
{'X': pars['coefficients'].astype(numpy.float32)},
outputs={'Y': numpy.float32},
target_opset=12)
oinf = OnnxInference(model_def)
pprint.pprint(oinf.to_sequence())
>>>
{'attributes': {},
'functions': {},
'inits': {},
'inputs': {'X': {'name': 'X',
'type': {'elem': 'float', 'kind': 'tensor', 'shape': (2,)}}},
'intermediate': {'Y': None},
'ir_version': 8,
'nodes': {'_linearregressor': Onnx-LinearRegressor(X) -> Y (name='_linearregressor')},
'outputs': {'Y': {'name': 'Y',
'type': {'elem': 'float',
'kind': 'tensor',
'shape': ('?',)}}},
'sequence': [Onnx-LinearRegressor(X) -> Y (name='_linearregressor')],
'statics': {},
'targets': {'ai.onnx.ml': 1}}
See an example of representation in notebook ONNX visualization.
(original entry : onnx_inference.py:docstring of mlprodict.onnxrt.onnx_inference.OnnxInference.to_sequence, line 5)
Convert a function into ONNX code
The following code parses a python function and returns another python function which produces an ONNX graph if executed.
<<<
import numpy
from mlprodict.onnx_tools.onnx_grammar import translate_fct2onnx
def trs(x, y):
z = x + numpy.transpose(y, axes=[1, 0])
return x * z
onnx_code = translate_fct2onnx(
trs, context={'numpy.transpose': numpy.transpose})
print(onnx_code)
>>>
def trs(x, y, dtype=numpy.float32, op_version=None):
z = (
OnnxAdd(
x,
OnnxTranspose(
y,
perm=[1, 0],
op_version=op_version
),
op_version=op_version
)
)
return (
OnnxMul(
x,
z,
op_version=op_version
)
)
(original entry : onnx_translation.py:docstring of mlprodict.onnx_tools.onnx_grammar.onnx_translation.translate_fct2onnx, line 23)
Convert a function into ONNX code and run
The following code parses a python function and returns
another python function which produces an ONNX
graph if executed. The example executes the function,
creates an ONNX then uses OnnxInference
to compute predictions. Finally it compares
them to the original.
<<<
import numpy
from mlprodict.onnx_tools.onnx_grammar import translate_fct2onnx
from mlprodict.plotting.text_plot import onnx_simple_text_plot
from mlprodict.onnxrt import OnnxInference
from mlprodict.npy.xop import loadop
OnnxAdd, OnnxTranspose, OnnxMul, OnnxIdentity = loadop(
'Add', 'Transpose', 'Mul', 'Identity')
ctx = {'OnnxAdd': OnnxAdd,
'OnnxTranspose': OnnxTranspose,
'OnnxMul': OnnxMul,
'OnnxIdentity': OnnxIdentity}
def trs(x, y):
z = x + numpy.transpose(y, axes=[1, 0])
return x * z
inputs = {'x': numpy.array([[1, 2]], dtype=numpy.float32),
'y': numpy.array([[-0.3, 0.4]], dtype=numpy.float32).T}
original = trs(inputs['x'], inputs['y'])
print('original output:', original)
onnx_fct = translate_fct2onnx(
trs, context={'numpy.transpose': numpy.transpose},
cpl=True, context_cpl=ctx, output_names=['Z'])
onnx_code = onnx_fct('x', 'y', op_version=12)
onnx_g = onnx_code.to_onnx(inputs, target_opset=12)
print("ONNX model")
print(onnx_simple_text_plot(onnx_g))
oinf = OnnxInference(onnx_g)
res = oinf.run(inputs)
print('-----------')
print("ONNX inference:", res['Z'])
>>>
original output: [[0.7 4.8]]
ONNX model
opset: domain='' version=12
input: name='x' type=dtype('float32') shape=[1, 2]
input: name='y' type=dtype('float32') shape=[2, 1]
Transpose(y, perm=[1,0]) -> out_tra_0
Add(x, out_tra_0) -> out_add_0
Mul(x, out_add_0) -> Z
output: name='Z' type=dtype('float32') shape=[1, 2]
-----------
ONNX inference: [[0.7 4.8]]
(original entry : onnx_translation.py:docstring of mlprodict.onnx_tools.onnx_grammar.onnx_translation.translate_fct2onnx, line 49)
Converts bytes into an array (serialization)
Useful to deserialize.
<<<
import numpy
from mlprodict.onnx_tools.onnx2py_helper import to_bytes, from_bytes
data = numpy.array([[0, 1], [2, 3], [4, 5]], dtype=numpy.float32)
pb = to_bytes(data)
data2 = from_bytes(pb)
print(data2)
>>>
[[0. 1.]
[2. 3.]
[4. 5.]]
(original entry : onnx2py_helper.py:docstring of mlprodict.onnx_tools.onnx2py_helper.from_bytes, line 6)
Displays an ONNX graph as text
The function uses an adjacency matrix of the graph. Results are displayed by rows, operator by columns. Results kinds are shows on the left, their names on the right. Operator types are displayed on the top, their names on the bottom.
<<<
import numpy
from mlprodict.onnx_conv import to_onnx
from mlprodict import __max_supported_opset__ as opv
from mlprodict.tools.graphs import onnx2bigraph
from mlprodict.npy.xop import loadop
OnnxAdd, OnnxSub = loadop('Add', 'Sub')
idi = numpy.identity(2).astype(numpy.float32)
A = OnnxAdd('X', idi, op_version=opv)
B = OnnxSub(A, 'W', output_names=['Y'], op_version=opv)
onx = B.to_onnx({'X': idi, 'W': idi})
bigraph = onnx2bigraph(onx)
graph = bigraph.display_structure()
text = graph.to_text()
print(text)
>>>
somewhere/workspace/mlprodict/mlprodict_UT_39_std/_doc/sphinxdoc/source/mlprodict/npy/xop_variable.py:64: DeprecationWarning: `mapping.NP_TYPE_TO_TENSOR_TYPE` is now deprecated and will be removed in the next release or so.To silence this warning, please use `helper.{self._future_function}` instead.
return NP_TYPE_TO_TENSOR_TYPE[dtype]
somewhere/workspace/mlprodict/mlprodict_UT_39_std/_doc/sphinxdoc/source/mlprodict/npy/xop_variable.py:64: DeprecationWarning: `mapping.NP_TYPE_TO_TENSOR_TYPE` is now deprecated and will be removed in the next release or so.To silence this warning, please use `helper.{self._future_function}` instead.
return NP_TYPE_TO_TENSOR_TYPE[dtype]
A S
d u
d b
Input-0 I1 W
Input-1 I0 X
Init I1 init
inout O0 I0 out_add_0
Output-0 O0 Y
_ _
a s
d u
d b
(original entry : graphs.py:docstring of mlprodict.tools.graphs.onnx2bigraph, line 17)
Extract information from a model
The function analyze_model extracts global
figures about a model, whatever it is.
<<<
import pprint
from sklearn.datasets import load_iris
from sklearn.ensemble import RandomForestClassifier
from mlprodict.tools.model_info import analyze_model
data = load_iris()
X, y = data.data, data.target
model = RandomForestClassifier().fit(X, y)
infos = analyze_model(model)
pprint.pprint(infos)
>>>
{'classes_.shape': 3,
'estimators_.classes_.shape': 3,
'estimators_.max|tree_.max_depth': 10,
'estimators_.n_classes_': 3,
'estimators_.size': 100,
'estimators_.sum|tree_.leave_count': 877,
'estimators_.sum|tree_.node_count': 1654,
'n_classes_': 3}
(original entry : model_info.py:docstring of mlprodict.tools.model_info.analyze_model, line 8)
Get the tree of a simple function
The following code uses Python syntax but follows a SQL logic.
<<<
import ast
import inspect
from textwrap import dedent
from mlprodict.onnx_tools.onnx_grammar import CodeNodeVisitor
def norm2(x, y):
delta = x - y
n = delta ** 2
return n
code = dedent(inspect.getsource(norm2))
node = ast.parse(code)
v = CodeNodeVisitor()
v.visit(node)
for r in v.Rows:
print("{0}{1}: {2}".format(" " * r["indent"], r["type"], r["str"]))
>>>
Module:
FunctionDef: norm2
arguments:
arg: x
arg: y
Assign:
Name: delta
BinOp:
Name: x
Sub:
Name: y
Assign:
Name: n
BinOp:
Name: delta
Pow:
Num: 2
Return:
Name: n
(original entry : node_visitor_translator.py:docstring of mlprodict.onnx_tools.onnx_grammar.node_visitor_translator.CodeNodeVisitor, line 3)
Plot benchmark improvments
import matplotlib.pyplot as plt
from mlprodict.plotting.plotting_benchmark import plot_benchmark_metrics
data = {(1, 1): 0.1, (10, 1): 1, (1, 10): 2,
(10, 10): 100, (100, 1): 100, (100, 10): 1000}
fig, ax = plt.subplots(1, 2, figsize=(10, 4))
plot_benchmark_metrics(data, ax=ax[0], cbar_kw={'shrink': 0.6})
plot_benchmark_metrics(data, ax=ax[1], transpose=True,
xlabel='X', ylabel='Y',
cbarlabel="ratio")
plt.show()
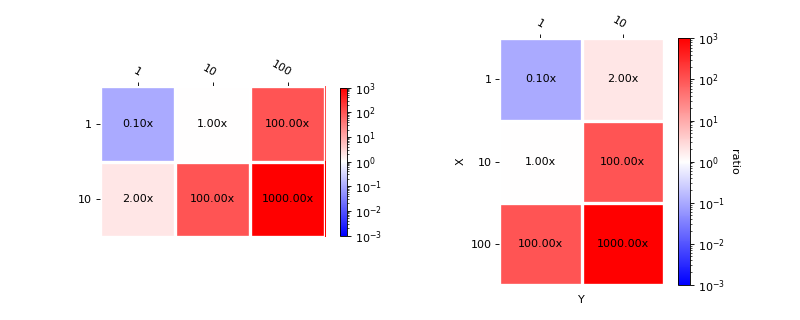
(original entry : plotting_benchmark.py:docstring of mlprodict.plotting.plotting_benchmark.plot_benchmark_metrics, line 18)
Run a model with runtime ‘python_compiled’
The following code trains a model and compute
the predictions with runtime 'python_compiled'.
It converts the onnx graph into a python function
which calls every operator. Its code is printed
below.
<<<
import numpy
from sklearn.datasets import load_iris
from sklearn.model_selection import train_test_split
from sklearn.ensemble import AdaBoostClassifier
from sklearn.tree import DecisionTreeClassifier
from mlprodict.onnx_conv import to_onnx
from mlprodict.onnxrt import OnnxInference
iris = load_iris()
X, y = iris.data, iris.target
X_train, X_test, y_train, __ = train_test_split(X, y, random_state=11)
y_train = y_train.astype(numpy.float32)
clr = AdaBoostClassifier(
base_estimator=DecisionTreeClassifier(max_depth=3),
n_estimators=3)
clr.fit(X_train, y_train)
model_def = to_onnx(clr, X_train.astype(numpy.float32),
target_opset=12)
oinf2 = OnnxInference(model_def, runtime='python_compiled')
print(oinf2.run({'X': X_test[:5]}))
# prints out the python function equivalent
# to the onnx graph
print(oinf2)
>>>
somewhere/.local/lib/python3.9/site-packages/sklearn/ensemble/_base.py:166: FutureWarning: `base_estimator` was renamed to `estimator` in version 1.2 and will be removed in 1.4.
warnings.warn(
{'output_label': array([2, 2, 1, 1, 2]), 'output_probability': []}
OnnxInference(...)
def compiled_run(dict_inputs, yield_ops=None, context=None, attributes=None):
if yield_ops is not None:
raise NotImplementedError('yields_ops should be None.')
# init: classes (classes)
# init: clip_min (clip_min)
# init: inverted_n_classes (inverted_n_classes)
# init: mul_operand (mul_operand)
# init: n_classes_minus_one (n_classes_minus_one)
# init: shape_tensor (shape_tensor)
# init: shape_tensor3 (shape_tensor3)
# init: zero_scalar (zero_scalar)
# inputs
X = dict_inputs['X']
(elab_name_1, eprob_name_1, ) = n0_treeensembleclassifier_1(X)
(elab_name_0, eprob_name_0, ) = n1_treeensembleclassifier_1(X)
(clipped_proba1, ) = n2_clip_11(eprob_name_1, clip_min)
(clipped_proba, ) = n3_clip_11(eprob_name_0, clip_min)
(log_proba1, ) = n4_log(clipped_proba1)
(log_proba, ) = n5_log(clipped_proba)
(reduced_proba1, ) = n6_reducesum_11(log_proba1)
(reduced_proba, ) = n7_reducesum_11(log_proba)
(reshaped_result1, ) = n8_reshape_5(reduced_proba1, shape_tensor)
(reshaped_result, ) = n9_reshape_5(reduced_proba, shape_tensor)
(prod_result1, ) = n10_mul(reshaped_result1, inverted_n_classes)
(prod_result, ) = n11_mul(reshaped_result, inverted_n_classes)
(sub_result1, ) = n12_sub(log_proba1, prod_result1)
(sub_result, ) = n13_sub(log_proba, prod_result)
(samme_proba, ) = n14_mul(sub_result, n_classes_minus_one)
(samme_proba1, ) = n15_mul(sub_result1, n_classes_minus_one)
(summation_prob, ) = n16_sum(samme_proba, samme_proba1)
(div_result, ) = n17_div(summation_prob, n_classes_minus_one)
(exp_operand, ) = n18_mul(div_result, mul_operand)
(exp_result, ) = n19_exp(exp_operand)
(reduced_exp_result, ) = n20_reducesum_11(exp_result)
(normaliser, ) = n21_reshape_5(reduced_exp_result, shape_tensor)
(cast_normaliser, ) = n22_cast(normaliser)
(comparison_result, ) = n23_equal(cast_normaliser, zero_scalar)
(cast_output, ) = n24_cast(comparison_result)
(zero_filtered_normaliser, ) = n25_add(normaliser, cast_output)
(probabilities, ) = n26_div(exp_result, zero_filtered_normaliser)
(argmax_output, ) = n27_argmax_12(probabilities)
(output_probability, ) = n28_zipmap(probabilities)
(array_feature_extractor_result, ) = n29_arrayfeatureextractor(classes, argmax_output)
(reshaped_result2, ) = n30_reshape_5(array_feature_extractor_result, shape_tensor3)
(label, ) = n31_cast(reshaped_result2)
(output_label, ) = n32_cast(label)
return {
'output_label': output_label,
'output_probability': output_probability,
}
(original entry : onnx_inference.py:docstring of mlprodict.onnxrt.onnx_inference.OnnxInference._build_compile_run, line 7)