Algo - simulation COVID#

Links: notebook, html, python, slides, GitHub

Ou comment utiliser les mathématiques pour comprendre la propagation de l’épidémie.

from jyquickhelper import add_notebook_menu
add_notebook_menu()

%matplotlib inline

Enoncé #

On récupère les données du COVID par région et par âge et premier graphe #

A cette adresse : Données relatives à l’épidémie de COVID-19 en France : vue d’ensemble

from pandas import read_csv, to_datetime
url = "https://www.data.gouv.fr/en/datasets/r/d3a98a30-893f-47f7-96c5-2f4bcaaa0d71"
covid = read_csv(url, sep=",")
covid['date'] = to_datetime(covid['date'])
covid.tail()

	date	total_cas_confirmes	total_deces_hopital	total_deces_ehpad	total_cas_confirmes_ehpad	total_cas_possibles_ehpad	patients_reanimation	patients_hospitalises	total_patients_gueris	nouveaux_patients_hospitalises	nouveaux_patients_reanimation
802	2022-05-13	NaN	118431	28826.0	NaN	NaN	1233.0	19272.0	653050.0	756.0	77.0
803	2022-05-14	NaN	118494	28837.0	NaN	NaN	1213.0	18901.0	653734.0	387.0	42.0
804	2022-05-15	NaN	118508	28844.0	NaN	NaN	1214.0	18935.0	653827.0	145.0	13.0
805	2022-05-16	NaN	118633	28845.0	NaN	NaN	1199.0	18742.0	654775.0	900.0	94.0
806	2022-05-17	NaN	118723	28845.0	NaN	NaN	1173.0	18290.0	655984.0	883.0	106.0

ax = covid.set_index("date").plot(
    title="Evolution des hospitalisations par jour", figsize=(14, 4))
ax.set_yscale("log");

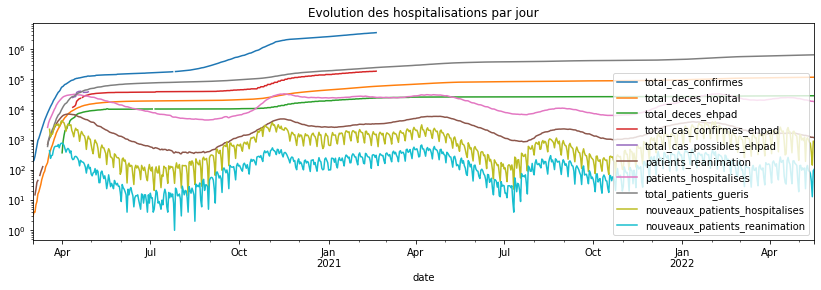
Il y a quelques valeurs manquantes même pour les séries aggrégées… Comme je n’ai pas le courage de corriger les valeurs unes à unes, je prends un autre fichier et quelques aberrations comme le nombre de décès qui décroît, ce qui est rigoureusement impossible.

from pandas import concat, to_datetime

def extract_data(kind='deaths', country='France'):
    url = (
        "https://raw.githubusercontent.com/CSSEGISandData/COVID-19/"
        "master/csse_covid_19_data/"
        "csse_covid_19_time_series/time_series_covid19_%s_global.csv" %
        kind)
    df = read_csv(url)
    eur = df[df['Country/Region'].isin([country])
             & df['Province/State'].isna()]
    tf = eur.T.iloc[4:]
    tf.columns = [kind]
    return tf

def extract_whole_data(kind=['deaths', 'confirmed', 'recovered'],
                       country='France'):
    population = {
        'France': 67e6,
    }

    total = population[country]
    dfs = []
    for k in kind:
        df = extract_data(k, country)
        dfs.append(df)
    conc = concat(dfs, axis=1)
    conc['infected'] = conc['confirmed'] - (conc['deaths'] + conc['recovered'])
    conc['safe'] = total - conc.drop('confirmed', axis=1).sum(axis=1)
    conc.index = to_datetime(conc.index)

    return conc

covid = extract_whole_data()
covid.tail()

	deaths	confirmed	infected	safe
2022-11-29	155309	36762891	36607582	30237109.0
2022-11-30	155384	36829869	36674485	30170131.0
2022-12-01	155459	36897875	36742416	30102125.0
2022-12-02	155526	36955945	36800419	30044055.0
2022-12-03	155526	36955945	36800419	30044055.0

import matplotlib.pyplot as plt
fig, ax = plt.subplots(1, 2, figsize=(14, 4))
covid[['confirmed', 'infected']].plot(title="Evolution de l'épidémie par jour", ax=ax[0])
covid[['deaths', 'recovered']].plot(title="Evolution de l'épidémie par jour", ax=ax[1]);

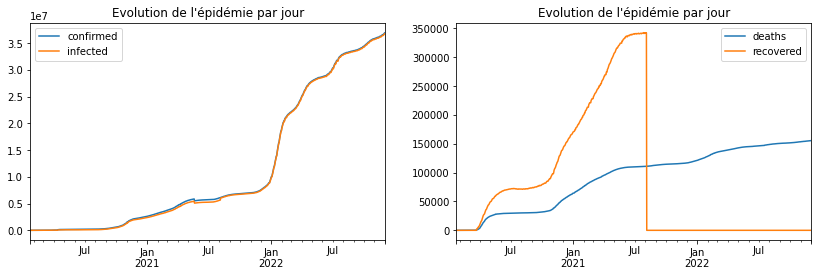
Même aberration, un nombre décès qui décroît… Il faudrait comprendre pourquoi pour savoir comment réparer les données. Ou on improvise. Pour chaque observation $X_t < X_{t-1}$ , on calcule le ratio $\frac{X_{t}}{X_{t-1}}$ et on multiplie toutes les observations $i<t$ par ce ratio.

from tqdm import tqdm  # pour avoir une barre de progression

def correct_series(X):
    for t in range(1, X.shape[0]):
        if X[t-1] > 0 and X[t] == 0:
            X[t] = X[t-1]
            continue
        if X[t] >= X[t-1] and X[t] < X[t-1] + 200000:
            continue
        ratio = X[t] / X[t-1]
        for i in range(0, t):
            X[i] *= ratio

covid_modified = covid.copy()
for c in tqdm(covid.columns):
    values = covid_modified[c].values
    correct_series(values)
    covid_modified[c] = values

covid_modified.tail()

100%|██████████| 5/5 [00:00<00:00, 29.74it/s]

	deaths	confirmed	recovered	infected	safe
2022-11-29	155309	36762891	342253	36607582	30044055.0
2022-11-30	155384	36829869	342253	36674485	30044055.0
2022-12-01	155459	36897875	342253	36742416	30044055.0
2022-12-02	155526	36955945	342253	36800419	30044055.0
2022-12-03	155526	36955945	342253	36800419	30044055.0

fig, ax = plt.subplots(1, 2, figsize=(14, 4))
covid_modified[['confirmed', 'infected']].plot(title="Evolution de l'épidémie par jour", ax=ax[0])
covid_modified[['deaths', 'recovered']].plot(title="Evolution de l'épidémie par jour", ax=ax[1]);

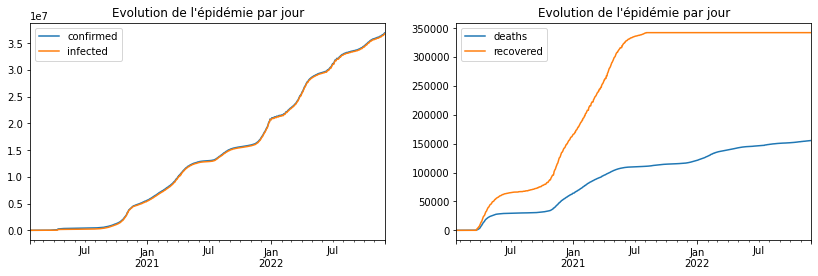
C’est mieux.

covid = covid_modified

On lisse.

lisse = covid.rolling(7).mean()
fig, ax = plt.subplots(1, 2, figsize=(14, 4))
lisse[['confirmed', 'infected']].plot(title="Evolution de l'épidémie par jour", ax=ax[0])
lisse[['deaths', 'recovered']].plot(title="Evolution de l'épidémie par jour", ax=ax[1]);

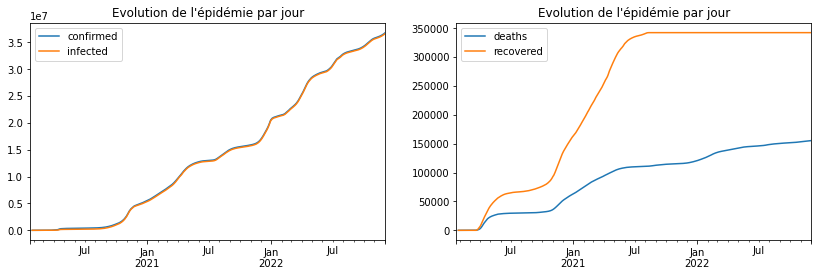
La série des recovered ne compte vraisemblablement que ceux qui sont passés à l’hôpital. Il faudrait recouper avec d’autres données pour être sûr. Ce sera pour un autre jour.

Modèle SIRD #

Pour en savoir plus Modèles compartimentaux en épidémiologie. On classe la population en quatre catégories :

S : personnes non contaminées
I : nombre de personnes malades ou contaminantes
R : personnes guéries (recovered)
D : personnes décédées

Les gens changent de catégorie en fonction de l’évolution de l’épidémie selon les équations qui suivent :

$\frac{dS}{dt} = - \beta \frac{S I}{N}$
$\frac{dI}{dt} = \frac{\beta S I}{N} - \mu I - \nu I$
$\frac{dD}{dt} = \nu I$
$\frac{dR}{dt} = \mu I$

$\beta$ est lié au taux de transmission, $\frac{1}{\mu}$ est la durée moyenne jusqu’à guérison, $\frac{1}{\nu}$ est la durée moyenne jusqu’au décès.

Q0 : une petite fonction pour dessiner #

Cette fonction servira à représenter graphiquement les résultats.

from datetime import datetime, timedelta


def plot_simulation(sim, day0=datetime(2020, 1, 1), safe=True,
                    ax=None, title=None, logy=False, two=False,
                    true_data=None):
    """
    On suppose que sim est une matrice (days, 4).
    :param sim: la simulation
    :param day0: le premier jour de la simulation (une observation par jour)
    :param safe: ajouter les personnes *safe* (non infectées), comme elles sont nombreuses,
        il vaut mieux aussi cocher *logy=True* pour que cela soit lisible
    :param ax: axes existant (utile pour superposer), None pour un créer un nouveau
    :param title: titre du graphe
    :param logy: échelle logarithmique sur l'axe des y
    :param two: faire deux graphes plutôt qu'un seul pour plus de visibilité
    :param true_data: vraies données à tracer également en plus de celle de la simulation
    :return: ax
    """
    df = DataFrame(sim, columns=['S', 'I', 'R', 'D'])
    # On ajoute des dates.
    df["date"] = [day0 + timedelta(d) for d in range(0, df.shape[0])]
    df = df.set_index("date")
    if true_data is None:
        tdf = None
    else:
        tdf = DataFrame(true_data, columns=['Sobs', 'Iobs', 'Robs', 'Dobs'])
        tdf["date"] = [day0 + timedelta(d) for d in range(0, tdf.shape[0])]
        tdf = tdf.set_index("date")

    if two:
        if ax is None:
            fig, ax = plt.subplots(1, 2, figsize=(14, 4))
        if safe:
            if tdf is not None:
                tdf.drop(['Dobs'], axis=1).plot(ax=ax[0], logy=logy, linewidth=8)
            df.drop('D', axis=1).plot(ax=ax[0], title=title, logy=logy, linewidth=4)
        else:
            if tdf is not None:
                tdf.drop(['Sobs', 'Dobs'], axis=1).plot(ax=ax[0], logy=logy, linewidth=8)
            df.drop(['S', 'D'], axis=1).plot(ax=ax[0], title=title, logy=logy, linewidth=4)
        if tdf is not None:
            tdf['Dobs'].plot(ax=ax[1], title=title, logy=logy, linewidth=8)
        df[['D']].plot(ax=ax[1], title='Décès', logy=logy, linewidth=4)
        ax[0].legend()
        ax[1].legend()
    else:
        if ax is None:
            fig, ax = plt.subplots(1, 1, figsize=(14, 4))
        if safe:
            if tdf is not None:
                tdf.plot(ax=ax, title=title, logy=logy, linewidth=8)
            df.plot(ax=ax, title=title, logy=logy, linewidth=4)
        else:
            if tdf is not None:
                tdf.drop(['Sobs'], axis=1).plot(ax=ax, title=title, logy=logy, linewidth=8)
            df.drop(['S'], axis=1).plot(ax=ax, title=title, logy=logy, linewidth=4)
        ax.legend()
    return ax

Q1 : écrire une fonction qui calcule la propagation #

On suppose que $\beta, \mu, \nu, S_0, I_0, R_0, D_0$ sont connus. On rappelle le modèle :

$dS = - \beta \frac{S I}{N}$
$dI = \frac{\beta S I}{N} - \mu I - \nu I$
$dD = \nu I$
$dR = \mu I$

import numpy

beta = 0.5
mu = 1./14
nu = 1./21
S0 = 9990
I0 = 10
R0 = 0
D0 = 0

Il faudra compléter le petit programme suivant :

from pandas import DataFrame



def simulation(beta, mu, nu, S0, I0, R0, D0, days=14):
    res = numpy.empty((days+1, 4), dtype=numpy.float64)
    res[0, :] = [S0, I0, R0, D0]
    N = sum(res[0, :])
    for t in range(1, res.shape[0]):
        dR = res[t-1, 1] * mu
        # ....
    return res


sim = simulation(beta, mu, nu, S0, I0, R0, D0, 30)
plot_simulation(sim);

Q2 : on veut estimer les paramètres du modèle, une fonction d’erreur ?#

C’est compliqué parce que… les paramètres évoluent au cours du temps, en fonction du comportement des gens, masque, pas masque, confinement, reconfinement, température, manque de tests également… Tout d’abord les vraies données.

lisse_mars = lisse[30:]
dates = lisse_mars.index
france = numpy.zeros((lisse_mars.shape[0], 4), dtype=numpy.dtype)
france[:, 3] = lisse_mars['deaths']
france[:, 2] = lisse_mars['recovered']
france[:, 0] = lisse_mars['safe']
france[:, 1] = lisse_mars['infected']

france[:5]

array([[29963471.89949666, 1.1640875027069664, 3.626756310367156,
        0.9858981877075415],
       [29963471.89949666, 1.1640875027069664, 3.626756310367156,
        0.9858981877075415],
       [29963471.89949666, 1.1640875027069664, 3.626756310367156,
        0.9858981877075415],
       [29963471.89949666, 1.1640875027069664, 3.626756310367156,
        0.9858981877075415],
       [29963471.89949666, 1.1640875027069664, 4.533445387958945,
        0.9858981877075415]], dtype=object)

plot_simulation(france, dates[0], safe=False, logy=True, title="Vraies données");

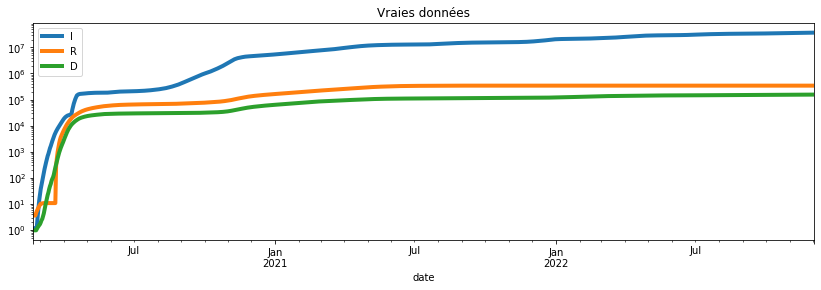
Et sur les derniers jours.

plot_simulation(france[-60:], dates[-60], two=True, safe=False, title="Vraies données, derniers mois");

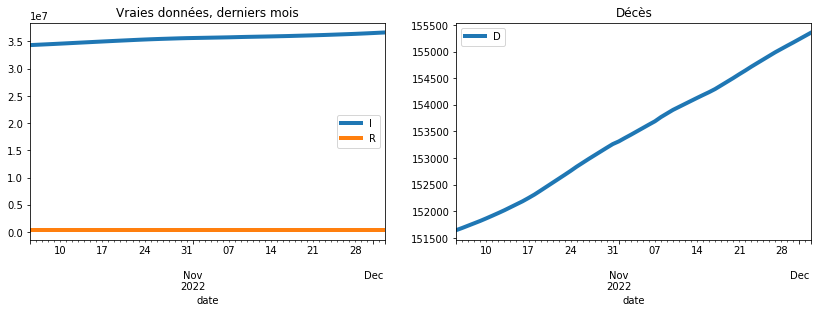
Bref, on part du principe que le modèle est plutôt fiable sur une courte période de temps, on tire plein de paramètres aléatoires et on regarde ce qui marche le mieux. Et pour comparer deux jeux de paramètres, il faut donc une fonction d’erreur qu’on prendra comme égal à la somme des erreurs de prédictions.

Maintenant il faut faire attention à ce qu’on compare. La simulation calcule les catégories de population au temps t, mais pas toujours les séries cumulées. La série des personnes contaminées est transitoire dans la simulation et cumulées dans les données récupérées. La première étape consiste à transformer les données simulées pour qu’elles soient comparables aux données collectées.

def simulation_cumulee(beta, mu, nu, S0, I0, R0, D0, days=14):
    # ...
    pass

Maintenant la fonction d’erreur :

def error(data, simulation):
    # ... à compléter
    return 0

Q3 : optimisation #

Pour optimiser, on tire des paramètres de façon aléatoire dans un intervalle donné et on choisit ceux qui minimisent l’erreur.

from tqdm import tqdm  # pour avoir une barre de progression


def optimisation(true_data, i_range=(0, 0.2), beta_range=(0, 0.5),
                 mu_range=(0., 0.2), nu_range=(0., 0.2),
                 max_iter=1000, error_fct=error):
    N = sum(true_data[0, :])
    rnd = numpy.random.rand(max_iter, 4)
    for i, (a, b) in enumerate([i_range, beta_range, mu_range, nu_range]):
        rnd[:, i] = rnd[:, i] # à compléter ...

    err_min = None
    for it in tqdm(range(max_iter)):
        i, beta, mu, nu = rnd[it, :]

        D0 = true_data[0, 3]
        # dI0 =
        # S0 =
        # I0 =
        # R0 =
        sim = simulation_cumulee(beta, mu, nu, S0, I0, R0, D0, days=true_data.shape[0] - 1)
        err = error_fct(true_data, sim)
        if err_min is None or err < err_min:
            # à compléter
            pass
    return best

Q4 : dessiner les résultats #

Q5 : vérifier que cela marche sur des données synthétiques #

On simule, on vérifie que l’optimisation retrouve les paramètres de la simulation.

Q6 : sur des données réelles #

Réponses #

Q1 : propagation #

On l’applique aux données réelles.

from datetime import datetime, timedelta
from pandas import DataFrame


def simulation(beta, mu, nu, S0, I0, R0, D0, days=14):
    res = numpy.empty((days+1, 4), dtype=numpy.float64)
    res[0, :] = [S0, I0, R0, D0]
    N = sum(res[0, :])
    for t in range(1, res.shape[0]):
        dR = res[t-1, 1] * mu
        dD = res[t-1, 1] * nu
        dI = res[t-1, 0] * res[t-1, 1] / N * beta
        res[t, 0] = res[t-1, 0] - dI
        res[t, 1] = res[t-1, 1] + dI - dR - dD
        res[t, 2] = res[t-1, 2] + dR
        res[t, 3] = res[t-1, 3] + dD
    return res


beta = 0.5
mu = 1./14
nu = 1./21
S0 = 9990
I0 = 10
R0 = 0
D0 = 0

sim = simulation(beta, mu, nu, S0, I0, R0, D0, 60)
plot_simulation(sim, dates[60], safe=False, two=True,
                title="Simulation pour essayer");

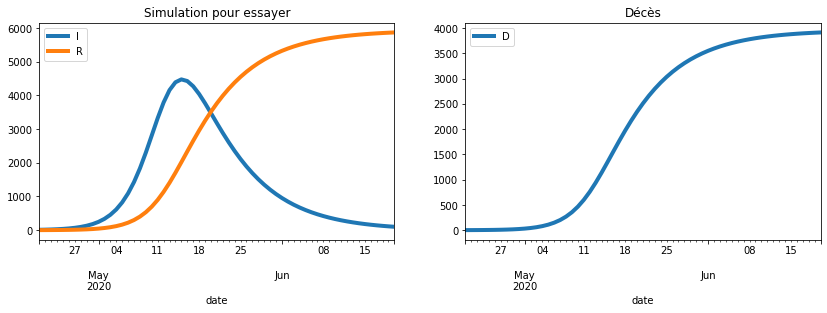
Q2 : série cumulées et fonction erreur #

On doit d’abord calculer la simulation qui modifie $I_t$ en $J_t$ qui correspond à l’ensemble des personnes contaminées jusqu’à présent.

def simulation_cumulee(beta, mu, nu, S0, I0, R0, D0, days=14):
    res = numpy.empty((days+1, 4), dtype=numpy.float64)
    cum = numpy.empty((days+1, 1), dtype=numpy.float64)
    res[0, :] = [S0, I0, R0, D0]
    cum[0, 0] = I0
    N = sum(res[0, :])
    for t in range(1, res.shape[0]):
        dR = res[t-1, 1] * mu
        dD = res[t-1, 1] * nu
        dI = res[t-1, 0] * res[t-1, 1] / N * beta
        res[t, 0] = res[t-1, 0] - dI
        res[t, 1] = res[t-1, 1] + dI - dR - dD
        res[t, 2] = res[t-1, 2] + dR
        res[t, 3] = res[t-1, 3] + dD
        cum[t, 0] = cum[t-1, 0] + dI
    res[:, 1] = cum[:, 0]
    return res

beta = 0.5
mu = 1./14
nu = 1./21
S0 = 9990
I0 = 10
R0 = 0
D0 = 0

sim = simulation_cumulee(beta, mu, nu, S0, I0, R0, D0, 60)
plot_simulation(sim, dates[60], safe=False, two=True,
                title="Simulation pour essayer");

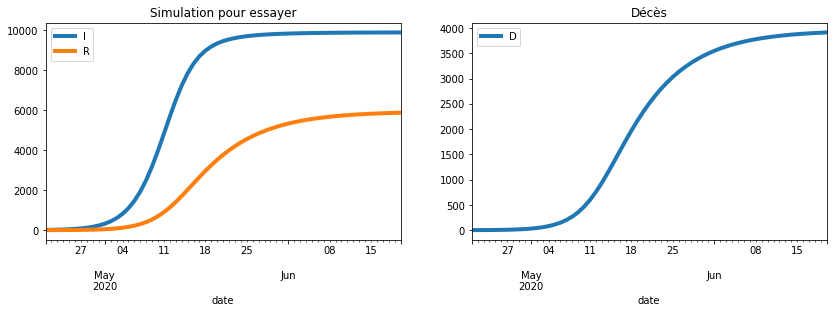
On compare avec les vraies données en gras.

beta = 0.04
mu = 0.03
nu = 0.0001
S0, I0, R0, D0 = france[120, :]
sim = simulation_cumulee(beta, mu, nu, S0, I0, R0, D0, 120)
plot_simulation(sim, dates[120], safe=False, two=True, true_data=france[120:240],
                title="Simulation et vraies données (en gros)");

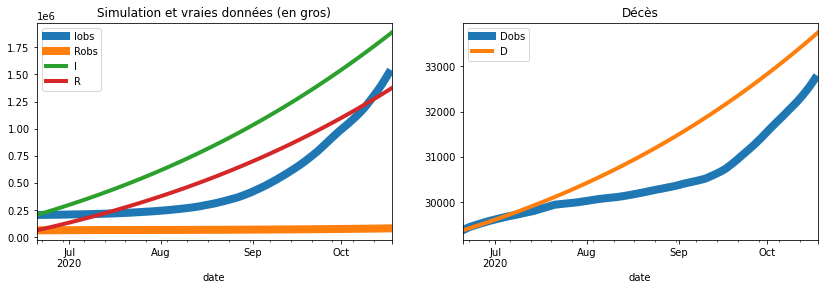
Pas simple de choisir des paramètres pour approximer la courbe.

def error(data, simulation):
    err = (data[:, 1] - simulation[:, 1]) ** 2 + (data[:, 3] - simulation[:, 3]) ** 2
    total = (numpy.sum(err) / data.shape[0]) ** 0.5
    return total


beta = 0.5
mu = 1./14
nu = 1./21
S0 = 9990
I0 = 10
R0 = 0
D0 = 0

sim = simulation_cumulee(beta, mu, nu, S0, I0, R0, D0, 30)
plot_simulation(sim);

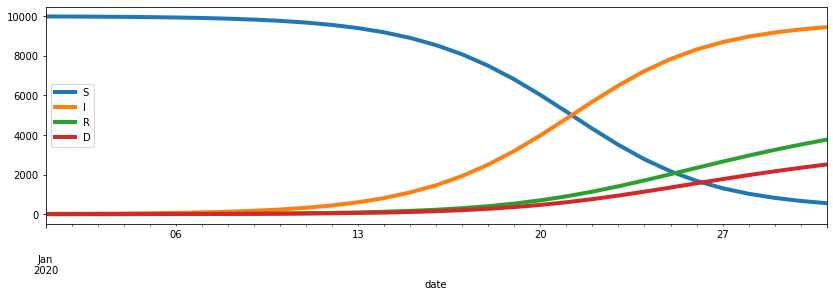
On regarde si on arrive à retrouver les paramètres de la simulation.

Q3, Q4, Q5 : optimisation sur des données synthétiques #

from tqdm import tqdm  # pour avoir une barre de progression


def optimisation(true_data, i_range=(0, 0.2), beta_range=(0, 0.5),
                 mu_range=(0., 0.2), nu_range=(0., 0.2),
                 max_iter=1000, error_fct=error):
    N = sum(true_data[0, :])
    rnd = numpy.random.rand(max_iter, 4)
    for i, (a, b) in enumerate([i_range, beta_range, mu_range, nu_range]):
        rnd[:, i] = rnd[:, i] * (b - a) + a
    err_min = None
    for it in tqdm(range(max_iter)):
        i, beta, mu, nu = rnd[it, :]
        dI0 = true_data[0, 0] * i
        D0 = true_data[0, 3]
        S0 = true_data[0, 0] - dI0
        I0 = true_data[0, 1] + dI0
        R0 = N - D0 - I0 - S0
        sim = simulation_cumulee(beta, mu, nu, S0, I0, R0, D0, days=true_data.shape[0] - 1)
        err = error_fct(true_data, sim)
        if err_min is None or err < err_min:
            err_min = err
            best = dict(beta=beta, mu=mu, nu=nu, I0=I0, i=i,
                        S0=S0, R0=R0, D0=D0, err=err, sim=sim)
    return best


beta = 0.04
mu = 0.07
nu = 0.04
S0 = 67e6
I0 = 100000
R0 = 10000
D0 = 10000
sim = simulation_cumulee(beta, mu, nu, S0, I0, R0, D0, 30)


res = optimisation(sim, max_iter=2000, error_fct=error, i_range=(0., 0.001))
sim_opt = res['sim']
del res['sim']
plot_simulation(sim_opt, dates[90], safe=False, two=True, true_data=sim,
                title="beta=%1.3f mu=%1.3f nu=%1.3f err=%1.3g i=%1.3g" % (
                    res['beta'], res['mu'], res['nu'], res['err'], res['i']));

100%|██████████| 2000/2000 [00:00<00:00, 7060.32it/s]

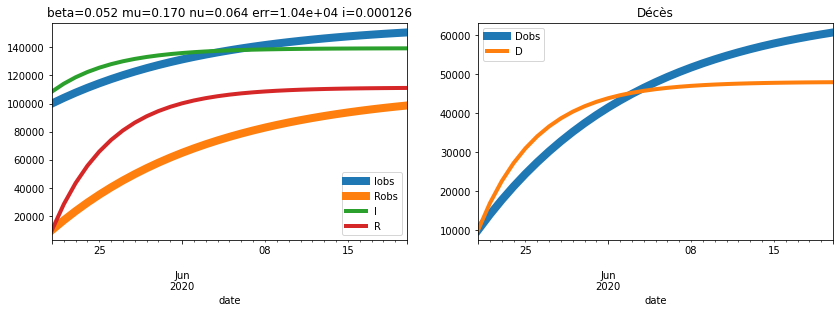
Ca ne marche pas trop mal.

Q6 : sur des données réelles #

res = optimisation(france[180:], error_fct=error, i_range=(0, 0.0001))
sim = res['sim']
del res['sim']
plot_simulation(sim, dates[180], safe=False, two=True, true_data=france[180:],
                title="beta=%1.3f mu=%1.3f nu=%1.3f err=%1.3f i=%1.3f" % (
                    res['beta'], res['mu'], res['nu'], res['err'], res['i']));

100%|██████████| 1000/1000 [00:03<00:00, 329.94it/s]

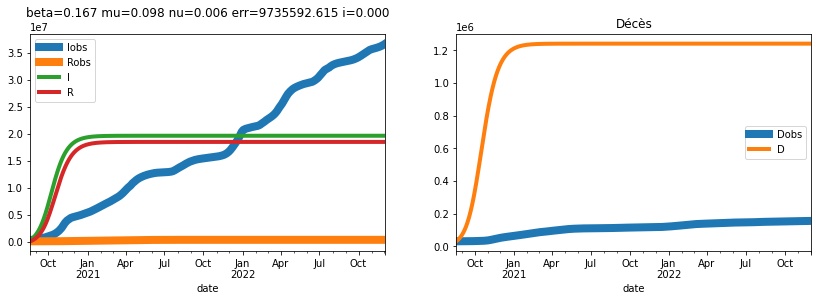
Ca ne marche pas super. On peut modifier l’erreur pour donner plus d’importance à la courbe des morts.

def error_norm(data, simulation):
    m1 = numpy.max(simulation[:, 1])
    m3 = numpy.max(simulation[:, 3])
    err = (data[:, 1] - simulation[:, 1]) ** 2 / m1 ** 2 + (data[:, 3] - simulation[:, 3]) ** 2 / m3 ** 2
    total = (numpy.sum(err) / data.shape[0]) ** 0.5
    return total

res = optimisation(france[150:], error_fct=error_norm, i_range=(0, 0.001))
sim = res['sim']
del res['sim']
plot_simulation(sim, dates[150], safe=False, two=True, true_data=france[150:],
                title="beta=%1.3f mu=%1.3f nu=%1.3f err=%1.3f i=%1.3f" % (
                    res['beta'], res['mu'], res['nu'], res['err'], res['i']));

100%|██████████| 1000/1000 [00:03<00:00, 314.34it/s]

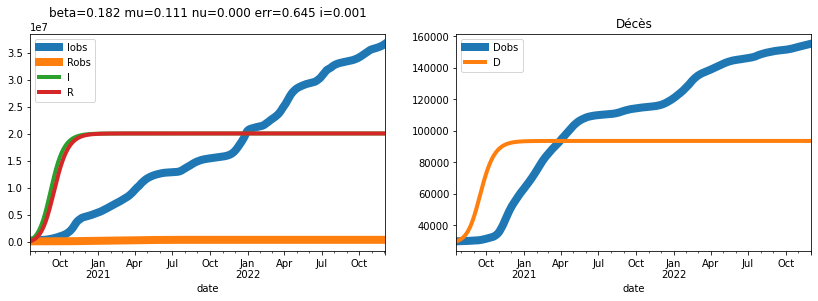
L’erreur est répartie sur l’ensemble de la courbe mais cela ne tient pas compte de la dynamique. Il faudrait prendre en compte les dérivées comme dans l’aticle A Modified SIR Model for the COVID-19 Contagion in Italy. Ou partir sur une approche plus directe comme celle proposée dans l’article Estimating and Simulating a SIRD Model of COVID-19 for Many Countries, States, and Cities. $\frac{dS}{dt} = - \beta \frac{S I}{N}$ implique que $\Delta(S_t) = S_{t+1} - S_t = -\beta \frac{S_t I_t}{N}$ . On peut alors calculer une sorte de $\beta_t$ dépendant du temps : $\beta_t = -N\frac{S_{t+1} - S_t}{S_t I_t}$ . Le problème, c’est $I_t$ qu’on ne connaît pas puisque c’est le nombre de personnes contaminantes à un instant t. On ne connaît pas plus $S_t$ mais on peut le déduire si on connaît $I_t$ . Cela dit, le paramètre $\nu$ est plus ou moins connu puisqu’il s’agit de l’inverse de la durée moyenne d’incubation jusqu’au décès. De là, on peut retrouver $\beta$ . On poursuit en passant au logarithme $\ln \beta_t = \ln N + \ln (S_t - S_{t+1}) - \ln S_t - \ln I_t$ . Le nombre de cas positifs découverts chaque jour correspond à $S_t - S_{t+1}$ . On ajoute que $\forall t, N = S_t + I_t + R_t + D_t$ et $D_{t+1} - D_t = \nu I_t$ . Donc :

$\ln \beta_t = \ln N + \ln (S_t - S_{t+1}) - \ln (S_t - S_{t-1} + S_{t-1}) - \ln (D_{t+1} - D_t) + \ln \nu$

Il y a deux inconnues, $\ln \beta - \ln \nu$ qu’on suppose constant pendant la période et $S_{t-1}$ . Il suffit d’écrire ces équations sur quelques jours puis de résoudre le système d’équations.

$\begin{array}{l} \ln \beta - \ln \nu = \ln N + \ln (S_t - S_{t+1}) - \ln (S_t - S_{t-1} + S_{t-1}) - \ln (D_{t+1} - D_t) \\ \ln \beta - \ln \nu = \ln N + \ln (S_{t+1} - S_{t+2}) - \ln (S_{t+1} - S_{t} + S_{t} - S_{t-1} + S_{t-1}) - \ln (D_{t+2} - D_{t+1}) \end{array}$

D’autres directions sont possibles comme The Parameter Identification Problem for SIR Epidemic Models: Identifying Unreported Cases qui propose d’estimer les paramètres sur une plus grande période.

D’autres articles : Introduction to inference: parameter estimation, Data-based analysis, modelling and forecasting of the COVID-19 outbreak, Identification and estimation of the SEIRD epidemic model for COVID-19.

Quelques liens :

Liens

Contenu

Information

Sujet précédent

Sujet suivant

Algo - simulation COVID#

Enoncé #

On récupère les données du COVID par région et par âge et premier graphe #

Modèle SIRD #

Q0 : une petite fonction pour dessiner #

Q1 : écrire une fonction qui calcule la propagation #

Q2 : on veut estimer les paramètres du modèle, une fonction d’erreur ?#

Q3 : optimisation #

Q4 : dessiner les résultats #

Q5 : vérifier que cela marche sur des données synthétiques #

Q6 : sur des données réelles #

Réponses #

Q1 : propagation #

Q2 : série cumulées et fonction erreur #

Q3, Q4, Q5 : optimisation sur des données synthétiques #

Q6 : sur des données réelles #

Liens

Information

Sujet précédent

Sujet suivant

Algo - simulation COVID#

Modèle SIRD#

Modèle SIRD #