Jeux de coloriage

Links: notebook, html, python, slides, GitHub

Le notebook explore quelques problèmes de géométrie dans un carré.

from jyquickhelper import add_notebook_menu
add_notebook_menu()

%matplotlib inline

Colorier un carré à proportion

On souhaite colorier 20% d’un carré. Facile !

import matplotlib.pyplot as plt
import matplotlib.patches as pch

def carre(ax=None):
    if ax is None:
        fig, ax = plt.subplots(1, 1, figsize=(2, 2))
    ax.plot([0, 0, 1, 1 ,0], [0, 1, 1, 0 ,0], 'k-')
    ax.set_title("Carré")
    return ax

ax = carre()
ax.add_patch(pch.Rectangle((0, 0), 0.2, 1, color="blue"));

Colorier en diagonale

import numpy
ax = carre()
ax.add_patch(pch.Polygon(numpy.array([(0, 0), (0.2, 0), (0, 0.2), (0, 0)]), color="blue"));

Moins facile…

Fonction de la surface couverte

def surface(x):
    if x <= 1.:
        return x**2 / 2
    if x <= 2.:
        return surface(1) + 0.5 - surface(2 - x)

fig, ax = plt.subplots(1, 1, figsize=(8, 4))
X = numpy.arange(0, 200) / 100
Y = [surface(x) for x in X]
ax.plot(X, Y)
ax.set_title("Surface diagonale en fonction de x")
ax.set_xlabel("x")
ax.set_ylabel("% couvert");

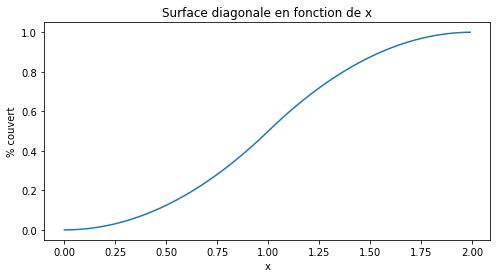
Ce qui nous intéresse en fait, c’est la réciproque de la fonction. Première version, sans savoir calculer mais en supposant qu’elle est croissante.

def surface_inverse(y, precision=1e-3):
    x = 0
    while x <= 2:
        s = surface(x)
        if s >= y:
            break
        x += precision
    return x - precision / 2

surface_inverse(0.2)

0.6325000000000005

fig, ax = plt.subplots(1, 1, figsize=(4, 4))
X = numpy.arange(0, 200) / 100
Y = [surface(x) for x in X]
ax.plot(X, Y, label="surface")
X2 = numpy.arange(0, 100) / 100
Y2 = [surface_inverse(x) for x in X2]
ax.plot(X2, Y2, label="surface_inverse")
ax.set_title("Surface diagonale en fonction de x")
ax.legend();

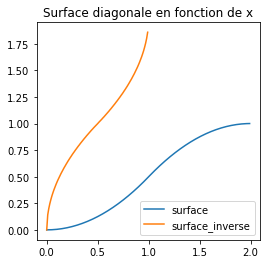
Ca marche mais…

%timeit surface(0.6)

357 ns ± 16.7 ns per loop (mean ± std. dev. of 7 runs, 1000000 loops each)

y = surface(0.6)
%timeit surface_inverse(y)

271 µs ± 27.4 µs per loop (mean ± std. dev. of 7 runs, 1000 loops each)

Et c’est de plus en plus long.

%timeit surface_inverse(y * 2)

399 µs ± 20.6 µs per loop (mean ± std. dev. of 7 runs, 1000 loops each)

Il y a plus court.

def surface_inverse_dicho(y, a=0., b=2., precision=1e-3):
    while abs(a - b) >= precision:
        m = (a + b) / 2.
        s = surface(m)
        if s >= y:
            b = m
        else:
            a = m
    return (a + b) / 2.

surface_inverse_dicho(0.2)

0.63232421875

fig, ax = plt.subplots(1, 1, figsize=(4, 4))
X = numpy.arange(0, 200) / 100
Y = [surface(x) for x in X]
ax.plot(X, Y, label="surface")
X2 = numpy.arange(0, 100) / 100
Y2 = [surface_inverse(x) for x in X2]
ax.plot(X2, Y2, label="surface_inverse")
X3 = numpy.arange(0, 100) / 100
Y3 = [surface_inverse_dicho(x) for x in X2]
ax.plot(X2, Y2, '.', label="surface_inverse_dicho")
ax.set_title("Surface diagonale en fonction de x")
ax.legend();

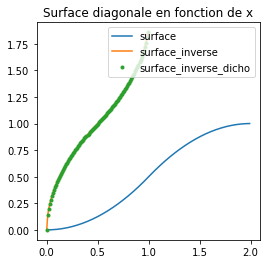
Ca marche.

y = surface(0.6)
%timeit surface_inverse_dicho(y)

6.9 µs ± 75.7 ns per loop (mean ± std. dev. of 7 runs, 100000 loops each)

%timeit surface_inverse_dicho(y * 2)

7.36 µs ± 216 ns per loop (mean ± std. dev. of 7 runs, 100000 loops each)

Près de 50 fois plus rapide et cela ne dépend pas de y cette fois-ci. Peut-on faire mieux ? On peut tabuler.

N = 100
table = {int(surface(x * 1. / N) * N): x * 1. / N for x in range(0, N+1)}

def surface_inv_table(y, N=N, precision=1e-3):
    i = int(y * N)
    a = table[i-1]
    b = table[i+1]
    return surface_inverse_dicho(y, a, b, precision=precision)

surface_inv_table(0.2)

0.63234375

y = surface(0.6)
%timeit surface_inv_table(y)

4.5 µs ± 199 ns per loop (mean ± std. dev. of 7 runs, 100000 loops each)

y = surface(0.6)
%timeit surface_inv_table(y * 2)

3.92 µs ± 87.1 ns per loop (mean ± std. dev. of 7 runs, 100000 loops each)

C’est mieux mais cette solution est un peu défectueuse en l’état, trouverez-vous pourquoi ? L’expression len(table) devrait vous y aider.

len(table)

51

Version mathématique

Pour cette fonction, on sait calculer la réciproque de façon exacte.

def surface(x):
    if x <= 1.:
        return x**2 / 2
    if x <= 2.:
        return surface(1) + 0.5 - surface(2 - x)

def surface_inv_math(y):
    if y <= 0.5:
        # y = x**2 / 2
        return (y * 2) ** 0.5
    else:
        # y = 1 - (2-x)**2 / 2
        return 2 - ((1 - y ) * 2) ** 0.5

surface_inv_math(0.2), surface_inv_math(0.8)

(0.6324555320336759, 1.3675444679663242)

y = surface(0.6)
%timeit surface_inv_math(y)

364 ns ± 10.5 ns per loop (mean ± std. dev. of 7 runs, 1000000 loops each)

y = surface(0.6)
%timeit surface_inv_math(y * 2)

434 ns ± 12.1 ns per loop (mean ± std. dev. of 7 runs, 1000000 loops each)

Il n’y a pas plus rapide mais cette option n’est pas toujours possible. Je passe la version écrite en C++, hors sujet pour le moment.

Retour au coloriage

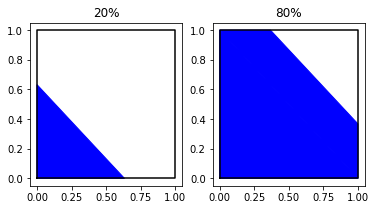
def coloriage_diagonale(y, ax=None):
    ax = carre(ax)
    if y <= 0.5:
        x = surface_inv_math(y)
        ax.add_patch(pch.Polygon(numpy.array([(0, 0), (x, 0), (0, x), (0, 0)]), color="blue"))
    else:
        ax.add_patch(pch.Polygon(numpy.array([(0, 0), (1, 0), (0, 1), (0, 0)]), color="blue"))
        x = surface_inv_math(y) - 1
        ax.add_patch(pch.Polygon(
            numpy.array([(1, 0), (1, x), (x, 1), (0, 1)]),
            color="blue"))
    return ax

fig, ax = plt.subplots(1, 2, figsize=(6, 3))
coloriage_diagonale(0.2, ax=ax[0])
coloriage_diagonale(0.8, ax=ax[1])
ax[0].set_title("20%")
ax[1].set_title("80%");

A quoi ça sert ?

Une programme est la concrétisation d’une idée et il y a souvent un compromis entre le temps passé à la réaliser et la performance qu’on souhaite obtenir. Et c’est souvent sans fin car les machines évoluent rapidement ces temps-ci.