Prédiction de la note des vins#

Links: notebook, html, PDF, python, slides, GitHub

Le notebook compare plusieurs de modèles de régression.

%matplotlib inline

import warnings
warnings.simplefilter('ignore')

from papierstat.datasets import load_wines_dataset
df = load_wines_dataset()
X = df.drop(['quality', 'color'], axis=1)
y = yn = df['quality']

from sklearn.model_selection import train_test_split
X_train, X_test, y_train, y_test = train_test_split(X, y)

On normalise les données.

from sklearn.preprocessing import normalize
X_train_norm = normalize(X_train)
X_test_norm = normalize(X_test)
X_norm = normalize(X)

Cette façon de faire est complètement erronnée car il est peu probable que la même normalisation soit apppliquée sur les trois bases. La normalisation doit être estimée sur la base d’apprentissage et appliquée sur la base de test. Reprenons.

from sklearn.preprocessing import Normalizer
norm = Normalizer()
X_train_norm = norm.fit_transform(X_train)
X_test_norm = norm.transform(X_test)
X_norm = norm.transform(X)

On récupère beaucoup de modèles implémentés dans scikit-learn pour la régression.

from sklearn.linear_model import *
from sklearn.ensemble import *
from sklearn.neighbors import *
from sklearn.neural_network import *

models = [
    model for name, model in globals().items() if (
        hasattr(model, 'fit') and not hasattr(model, 'predict_proba') and
        hasattr(model, '__name__') and not model.__name__.endswith('CV') and
        'Logistic' not in model.__name__ and 'Regr' in model.__name__)]

import pprint
pprint.pprint(models)

[<class 'sklearn.linear_model._bayes.ARDRegression'>,
 <class 'sklearn.linear_model._huber.HuberRegressor'>,
 <class 'sklearn.linear_model._base.LinearRegression'>,
 <class 'sklearn.linear_model._passive_aggressive.PassiveAggressiveRegressor'>,
 <class 'sklearn.linear_model._quantile.QuantileRegressor'>,
 <class 'sklearn.linear_model._stochastic_gradient.SGDRegressor'>,
 <class 'sklearn.linear_model._theil_sen.TheilSenRegressor'>,
 <class 'sklearn.linear_model._ransac.RANSACRegressor'>,
 <class 'sklearn.linear_model._glm.glm.PoissonRegressor'>,
 <class 'sklearn.linear_model._glm.glm.GammaRegressor'>,
 <class 'sklearn.linear_model._glm.glm.TweedieRegressor'>,
 <class 'sklearn.ensemble._forest.RandomForestRegressor'>,
 <class 'sklearn.ensemble._forest.ExtraTreesRegressor'>,
 <class 'sklearn.ensemble._bagging.BaggingRegressor'>,
 <class 'sklearn.ensemble._gb.GradientBoostingRegressor'>,
 <class 'sklearn.ensemble._weight_boosting.AdaBoostRegressor'>,
 <class 'sklearn.ensemble._voting.VotingRegressor'>,
 <class 'sklearn.ensemble._stacking.StackingRegressor'>,
 <class 'sklearn.ensemble._hist_gradient_boosting.gradient_boosting.HistGradientBoostingRegressor'>,
 <class 'sklearn.neighbors._regression.KNeighborsRegressor'>,
 <class 'sklearn.neighbors._regression.RadiusNeighborsRegressor'>,
 <class 'sklearn.neural_network._multilayer_perceptron.MLPRegressor'>]

from sklearn.metrics import r2_score

def score_model(xtr, xte, ytr, yte, model):
    try:
        model.fit(xtr, ytr)
    except Exception as e:
        raise Exception("Issue with model '{0}'".format(model.__name__)) from e
    return r2_score(yte, model.predict(xte))

from time import perf_counter
r2s = []
names = []
durations = []
regressors = {}
for i, model in enumerate(models):
    if model.__name__ in {'ARDRegression', 'VotingRegressor', 'StackingRegressor',
                          'QuantileRegressor'}:
        continue
    try:
        reg = model()
    except Exception as e:
        print('Skip', model)
        continue
    begin = perf_counter()
    r2 = score_model(X_train_norm, X_test_norm, y_train, y_test, reg)
    duree = perf_counter () - begin
    r2s.append(r2)
    names.append(model.__name__)
    durations.append(duree)
    regressors[model.__name__] = reg
    print(i, model.__name__, r2, duree)

HuberRegressor 0.18696322297535295 0.10263620000000007
LinearRegression 0.18670706392432423 0.0031078999999998302
PassiveAggressiveRegressor -2.4493503320572922 0.00904460000000018
SGDRegressor 0.014418866580130474 0.005636599999999881
TheilSenRegressor -0.22921086116095046 2.5755812999999996
RANSACRegressor -0.22456172730313217 0.10757049999999957
PoissonRegressor 0.0019476060926755245 0.008242899999999942
GammaRegressor 0.00035190831663889366 0.0046112000000002595
TweedieRegressor 0.00035356971012889815 0.00390669999999993
RandomForestRegressor 0.4902308886152582 3.781266499999999
ExtraTreesRegressor 0.5234939074444616 1.2828908000000006
BaggingRegressor 0.4275524601097942 0.3720353999999997
GradientBoostingRegressor 0.33578249602447263 2.3406590000000005
AdaBoostRegressor 0.19852494764300066 0.5364822
HistGradientBoostingRegressor 0.4116613218417975 1.8669652999999986
KNeighborsRegressor 0.17441896259812206 0.06659600000000054
RadiusNeighborsRegressor 0.00012107760711554949 0.7381427999999985
MLPRegressor 0.18147670458010268 4.3011114

import pandas
df = pandas.DataFrame(dict(model=names, r2=r2s, duree=durations))
df = df[['model', 'r2', 'duree']]
df.sort_values('r2')

	model	r2	duree
2	PassiveAggressiveRegressor	-2.449350	0.009045
4	TheilSenRegressor	-0.229211	2.575581
5	RANSACRegressor	-0.224562	0.107570
16	RadiusNeighborsRegressor	0.000121	0.738143
7	GammaRegressor	0.000352	0.004611
8	TweedieRegressor	0.000354	0.003907
6	PoissonRegressor	0.001948	0.008243
3	SGDRegressor	0.014419	0.005637
15	KNeighborsRegressor	0.174419	0.066596
17	MLPRegressor	0.181477	4.301111
1	LinearRegression	0.186707	0.003108
0	HuberRegressor	0.186963	0.102636
13	AdaBoostRegressor	0.198525	0.536482
12	GradientBoostingRegressor	0.335782	2.340659
14	HistGradientBoostingRegressor	0.411661	1.866965
11	BaggingRegressor	0.427552	0.372035
9	RandomForestRegressor	0.490231	3.781266
10	ExtraTreesRegressor	0.523494	1.282891

On filtre les valeurs inférieures à -1.

df = df[df.r2 >= -1]

import matplotlib.pyplot as plt
fig, ax = plt.subplots(figsize=(12, 4))
df.plot(x='duree', y='r2', kind="scatter", ax=ax)
for row in df.itertuples():
    t, y, x = row[1:4]
    if t[0] in {'B', 'L'}:
        ax.text(x, y, t, rotation=30, ha='left', va='bottom')
    else:
        ax.text(x, y, t, rotation=-40)
ax.set_title("Comparaison des modèles selon le temps d'apprentissage / r2");

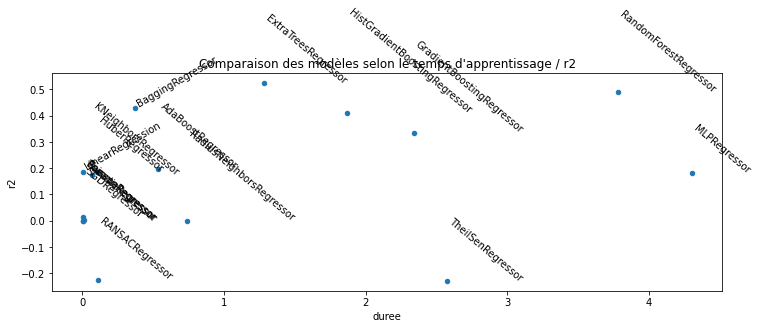
L’estimateur RANSACRegressor produit un $R^2$ très négatif. Regardons plus en détail.

pred = regressors['RANSACRegressor'].predict(X_test_norm)

import numpy.random
df = pandas.DataFrame(dict(pred=pred, expected=y_test))
df['expected'] += numpy.random.random(df.shape[0]) * 0.5
ax = df.plot(x="expected", y="pred", kind='scatter', figsize=(4, 4), linewidths=0.1)
ax.set_title('Graphe XY - valeurs attendues / prédites');

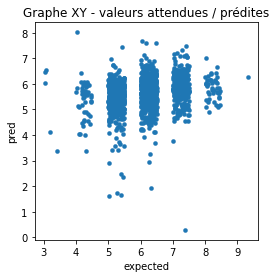
Essayons de voir avec la densité.

import seaborn
ax = seaborn.jointplot(df["expected"], df["pred"], kind="kde", size=4, space=0, ylim=(1, 9))
ax.ax_marg_y.set_title('Densité XY - valeur attendues / prédites');

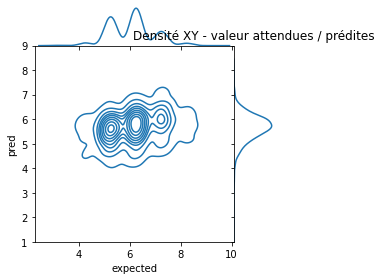
Pas facile à voir. Essayons de voir autrement en triant les prédictions et les valeurs attendues par ordre.

sv = df.sort_values(['expected', 'pred']).reset_index(drop=True)

import matplotlib.pyplot as plt
fig, ax = plt.subplots(figsize=(12, 3))
ax.plot(sv["pred"], label="RANSAC", lw=0.1)
ax.plot(list(sorted(df["expected"])), label="expected")
ax.plot(list(sorted(df["pred"])), label="RANSAC trié")
ax.set_ylim([0, 9])
ax.set_title('Valeur attendues et prédites triées par ordre croissant')
ax.legend();

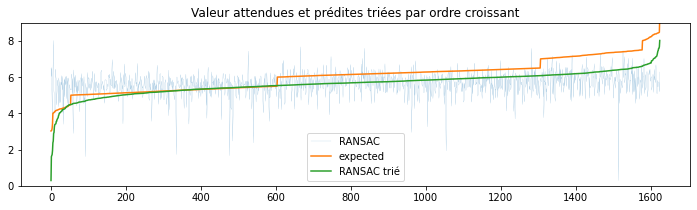
Le modèle est plutôt agité.

regressors['RANSACRegressor'].estimator_.intercept_

8.296147714878684

Pour s’assurer que les résultats sont fiables, il faut recommencer avec une validation croisée.

import numpy.random
rnd = numpy.random.permutation(range(X_norm.shape[0]))
xns = X_norm[rnd, :]
yns = yn[rnd]
xns.shape, yns.shape

((6497, 11), (6497,))

from sklearn.model_selection import cross_val_score

def score_model_cross(xn, yn, model):
    res = cross_val_score(model, xn, yn, cv=5)
    return res.mean(), min(res), max(res)

score_model_cross(xns, yns, LinearRegression())

(0.17975891799937466, 0.16696505316283117, 0.19857004070455042)

r2s = []
mis = []
mas = []
names = []
durations = []
regressors = {}
for i, model in enumerate(models):
    if model.__name__ in {'ARDRegression', 'VotingRegressor', 'QuantileRegressor'}:
        continue
    try:
        reg = model()
    except Exception as e:
        print('Skip', model)
        continue
    begin = perf_counter()
    r2, mi, ma = score_model_cross(xns, yns, reg)
    duree = perf_counter() - begin
    r2s.append(r2)
    mis.append(mi)
    mas.append(ma)
    names.append(model.__name__)
    durations.append(duree)
    regressors[model.__name__] = reg
    print(i, model.__name__, r2, mi, ma, "t=%r" % duree)

HuberRegressor 0.15926614746076234 0.14654481316725898 0.16913851017974213 t=0.454639499999999
LinearRegression 0.17975891799937466 0.16696505316283117 0.19857004070455042 t=0.016710999999997256
PassiveAggressiveRegressor -1.2023166987836942 -3.9867877266892178 0.1473069141592367 t=0.060205800000002085
SGDRegressor 0.008672768127243647 0.0021660038805777493 0.019095545791309232 t=0.03673420000000149
TheilSenRegressor -0.36938713022242337 -0.6323773846900367 -0.1285090090856622 t=12.1253441
RANSACRegressor -1.216541764611399 -2.1838034440150125 -0.49602375704620316 t=0.4227926000000011
PoissonRegressor 0.0005335331789835696 -0.00324272848486995 0.002202890520605516 t=0.041724600000002
GammaRegressor -0.0011833153140562436 -0.005003239249327773 0.00038081596763739345 t=0.03832559999999319
TweedieRegressor -0.0011890320765876484 -0.005037356583908137 0.0003836189724416572 t=0.03498609999999758
RandomForestRegressor 0.49573724359207744 0.47719555839567485 0.5195191337192313 t=20.5839067
ExtraTreesRegressor 0.5205178519581393 0.5088671068579345 0.544928615205679 t=6.329529699999995
BaggingRegressor 0.44200753753008665 0.4148201125863905 0.4665893219045759 t=1.9267918999999978
GradientBoostingRegressor 0.33429915333938653 0.31585334825211187 0.34981047673804344 t=8.977681399999994
AdaBoostRegressor 0.2087316189255112 0.19118571603372658 0.22096772688033828 t=1.8667038999999903
Skip <class 'sklearn.ensemble._stacking.StackingRegressor'>
HistGradientBoostingRegressor 0.4206957666044492 0.3909890965983751 0.4324440282212091 t=4.953426099999987
KNeighborsRegressor 0.17992428041726455 0.14412273193552394 0.2237578623112627 t=0.3946573999999998
RadiusNeighborsRegressor -0.0014925783119640545 -0.005365612415162646 0.00012185111722451403 t=3.9200797999999963
MLPRegressor 0.18770733115748367 0.15333935822510514 0.21342290214312276 t=20.982291099999998

df = pandas.DataFrame(dict(model=names, r2=r2s, min=mis, max=mas, duree=durations))
df = df[['model', 'r2', 'min', 'max', 'duree']]
df.sort_values('r2')

	model	r2	min	max	duree
5	RANSACRegressor	-1.216542	-2.183803	-0.496024	0.422793
2	PassiveAggressiveRegressor	-1.202317	-3.986788	0.147307	0.060206
4	TheilSenRegressor	-0.369387	-0.632377	-0.128509	12.125344
16	RadiusNeighborsRegressor	-0.001493	-0.005366	0.000122	3.920080
8	TweedieRegressor	-0.001189	-0.005037	0.000384	0.034986
7	GammaRegressor	-0.001183	-0.005003	0.000381	0.038326
6	PoissonRegressor	0.000534	-0.003243	0.002203	0.041725
3	SGDRegressor	0.008673	0.002166	0.019096	0.036734
0	HuberRegressor	0.159266	0.146545	0.169139	0.454639
1	LinearRegression	0.179759	0.166965	0.198570	0.016711
15	KNeighborsRegressor	0.179924	0.144123	0.223758	0.394657
17	MLPRegressor	0.187707	0.153339	0.213423	20.982291
13	AdaBoostRegressor	0.208732	0.191186	0.220968	1.866704
12	GradientBoostingRegressor	0.334299	0.315853	0.349810	8.977681
14	HistGradientBoostingRegressor	0.420696	0.390989	0.432444	4.953426
11	BaggingRegressor	0.442008	0.414820	0.466589	1.926792
9	RandomForestRegressor	0.495737	0.477196	0.519519	20.583907
10	ExtraTreesRegressor	0.520518	0.508867	0.544929	6.329530

import matplotlib.pyplot as plt
fig, ax = plt.subplots(figsize=(12, 4))
df[df['min'] > -0.1].plot(x='duree', y='r2', kind="scatter", ax=ax)
for row in df.itertuples():
    t, y, mi, ma, x = row[1:6]
    if mi < -0.1:
        continue
    ax.plot([x, x], [mi, ma], color="black")
    if t[0] in {'B', 'L'}:
        ax.text(x, y, t, rotation=30, ha='left', va='bottom')
    else:
        ax.text(x, y, t, rotation=-40)
ax.set_ylim([-1, 1])
ax.set_title("Comparaison des modèles selon le temps d'apprentissage / r2\nValidation croisée");

Le modèle RANSAC est conçu pour apprendre un modèle linéaire et réduire l’ensemble d’apprentissage aux points non aberrants. Dans notre cas, vu le peu d’exemples pour les notes élevées, il est très probable que celles-ci disparaissent des observations choisies pour estimer le modèle : le modèle choisit d’évincer les exemples pour lesquels l’erreur est la plus grande en considérant que cela est une indication du fait qu’ils sont aberrants. Malgré cela, sa faible capacité à prévoir vient du fait que la majorité des vins ont une note entre 4 et 6 et que finalement, il y a peu de différences : ils sont tous moyens et la différence s’explique par d’autres facteurs comme le juge ayant donné la note.

Liens

Contenu

Information

Sujet précédent

Sujet suivant

Prédiction de la note des vins#