Graphes en machine learning - énoncé#
Links: notebook, html, PDF, python, slides, GitHub
Ce notebook propose une série de graphes qu’on utilise fréquemment dans un notebook lorsqu’on fait du machine learning. Cela comprend notamment la courbe ROC pour les problèmes de classification.
# Cette instruction peut annuler l'effect de la suivante.
# On la place en premier.
%load_ext pyensae
%matplotlib inline
import matplotlib.pyplot as plt
plt.style.use('ggplot')
from jyquickhelper import add_notebook_menu
add_notebook_menu()
Le module utilise des données issues de Wine Quality Data Set pour lequel on essaye de prédire la qualité du vin en fonction de ses caractéristiques chimiques.
from pyensae.datasource import download_data, DownloadDataException
uci = "https://archive.ics.uci.edu/ml/machine-learning-databases/wine-quality/"
try:
download_data("winequality-red.csv", url=uci)
download_data("winequality-white.csv", url=uci)
except DownloadDataException:
print("backup")
download_data("winequality-red.csv", website="xd")
download_data("winequality-white.csv", website="xd")
%head winequality-red.csv
"fixed acidity";"volatile acidity";"citric acid";"residual sugar";"chlorides";"free sulfur dioxide";"total sulfur dioxide";"density";"pH";"sulphates";"alcohol";"quality" 7.4;0.7;0;1.9;0.076;11;34;0.9978;3.51;0.56;9.4;5 7.8;0.88;0;2.6;0.098;25;67;0.9968;3.2;0.68;9.8;5 7.8;0.76;0.04;2.3;0.092;15;54;0.997;3.26;0.65;9.8;5 11.2;0.28;0.56;1.9;0.075;17;60;0.998;3.16;0.58;9.8;6 7.4;0.7;0;1.9;0.076;11;34;0.9978;3.51;0.56;9.4;5 7.4;0.66;0;1.8;0.075;13;40;0.9978;3.51;0.56;9.4;5 7.9;0.6;0.06;1.6;0.069;15;59;0.9964;3.3;0.46;9.4;5 7.3;0.65;0;1.2;0.065;15;21;0.9946;3.39;0.47;10;7 7.8;0.58;0.02;2;0.073;9;18;0.9968;3.36;0.57;9.5;7
import pandas
red_wine = pandas.read_csv("winequality-red.csv", sep=";")
red_wine["red"] = 1
white_wine = pandas.read_csv("winequality-white.csv", sep=";")
white_wine["red"] = 0
wines = pandas.concat([red_wine, white_wine])
wines.head()
| fixed acidity | volatile acidity | citric acid | residual sugar | chlorides | free sulfur dioxide | total sulfur dioxide | density | pH | sulphates | alcohol | quality | red | |
|---|---|---|---|---|---|---|---|---|---|---|---|---|---|
| 0 | 7.4 | 0.70 | 0.00 | 1.9 | 0.076 | 11.0 | 34.0 | 0.9978 | 3.51 | 0.56 | 9.4 | 5 | 1 |
| 1 | 7.8 | 0.88 | 0.00 | 2.6 | 0.098 | 25.0 | 67.0 | 0.9968 | 3.20 | 0.68 | 9.8 | 5 | 1 |
| 2 | 7.8 | 0.76 | 0.04 | 2.3 | 0.092 | 15.0 | 54.0 | 0.9970 | 3.26 | 0.65 | 9.8 | 5 | 1 |
| 3 | 11.2 | 0.28 | 0.56 | 1.9 | 0.075 | 17.0 | 60.0 | 0.9980 | 3.16 | 0.58 | 9.8 | 6 | 1 |
| 4 | 7.4 | 0.70 | 0.00 | 1.9 | 0.076 | 11.0 | 34.0 | 0.9978 | 3.51 | 0.56 | 9.4 | 5 | 1 |
On découpe en base d’apprentissage, base de test :
from sklearn.model_selection import train_test_split
X = wines[[c for c in wines.columns if c != "quality"]]
Y = wines["quality"]
x_train, x_test, y_train, y_test = train_test_split(X, Y, test_size=0.33, random_state=42)
type(x_train), type(y_train)
(pandas.core.frame.DataFrame, pandas.core.series.Series)
wines.shape, x_train.shape, y_train.shape
((6497, 13), (4352, 12), (4352,))
Exploration#
histogrammes#
fonction hist
%matplotlib inline
import matplotlib.pyplot as plt
plt.get_backend()
'module://ipykernel.pylab.backend_inline'
wines.hist(figsize=(12,12))
print("-")
-
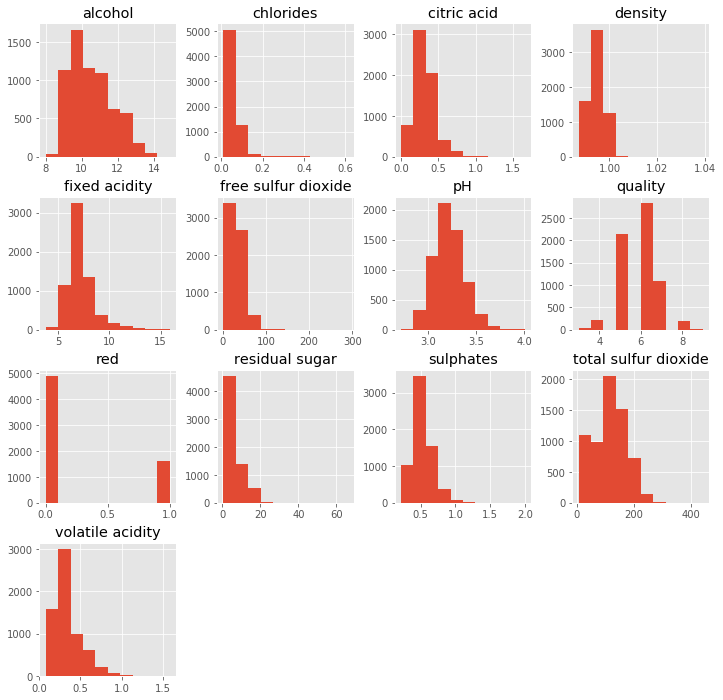
Et plus particulièrement :
wines.quality.hist(bins=7, figsize=(4,4))
<matplotlib.axes._subplots.AxesSubplot at 0x1c28eff0630>
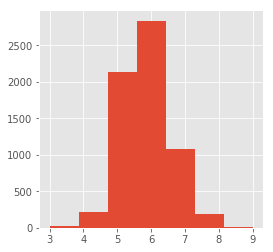
événements rares#
Les queues de distributions sont des événements rares. De même que dans cet échantillon, la classe 9 est très peu représentée (voir ci-dessous). Lorsqu’on découpe le jeu de données en base d’apprentissage et base de test, ces événements ne sont pas uniformément distribués. Il est très peu probable qu’un classifieur quelconque arrive à prédire la classe 9. Il faudra traiter cette classe séparément.
Il est difficile de dire si un prédicteur doit éviter d’utiliser des événements rares ou des valeurs aberrantes mais il est difficile de prévoir si la prédiction est généralisable. On choisit parfois de nettoyer les bases de ces événements, en les supprimant, en les lissant, en changeant d’échelle avec une échelle logarithmique.
wines[["quality", "red"]].groupby("quality").count()
| red | |
|---|---|
| quality | |
| 3 | 30 |
| 4 | 216 |
| 5 | 2138 |
| 6 | 2836 |
| 7 | 1079 |
| 8 | 193 |
| 9 | 5 |
corrélations#
fonction pairplot
import seaborn
seaborn.pairplot(wines)
<seaborn.axisgrid.PairGrid at 0x1c28dbc0ef0>
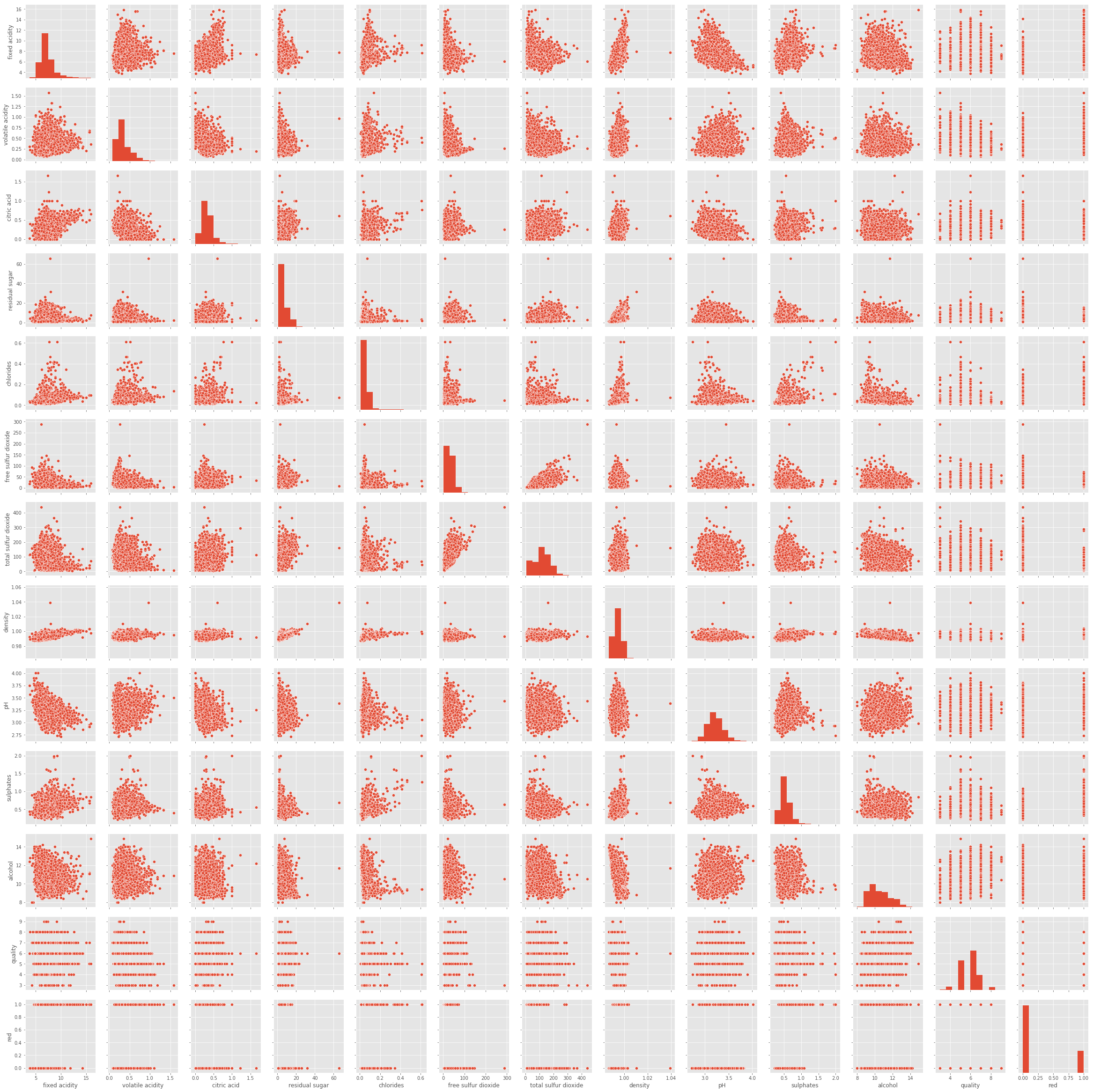
fonction clustermap, plus pratique quand il y a beaucoup de variables
import seaborn
seaborn.set(font="monospace")
cmap = seaborn.diverging_palette(h_neg=210, h_pos=350, s=90, l=30, as_cmap=True)
seaborn.clustermap(wines.corr(), linewidths=.5, figsize=(13, 13), cmap=cmap)
<seaborn.matrix.ClusterGrid at 0x1c298837da0>
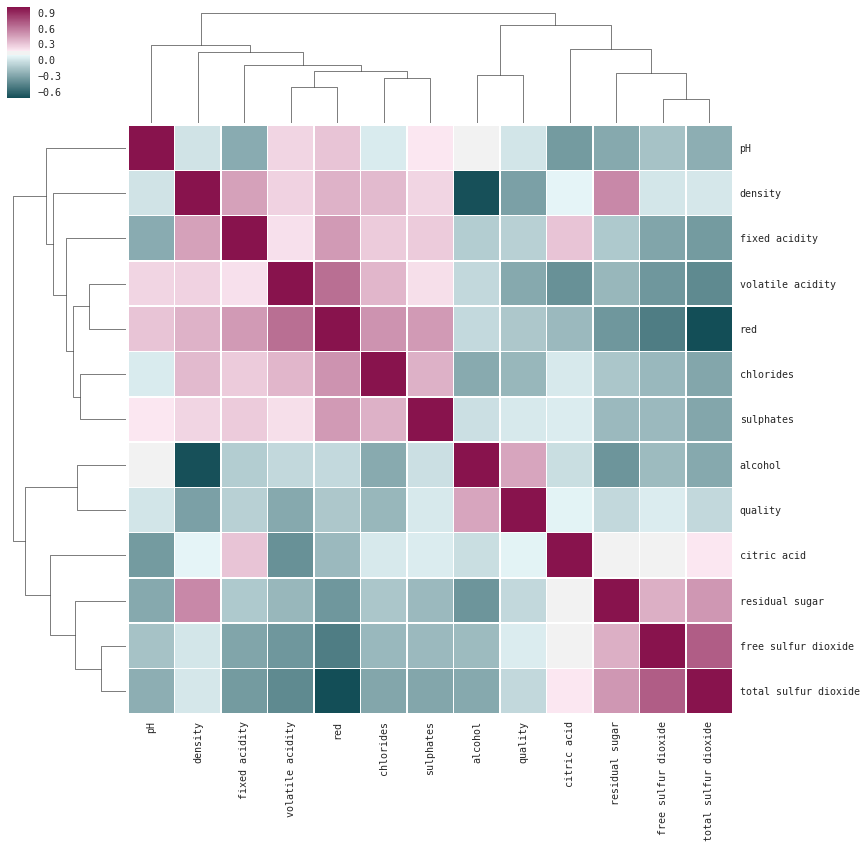
Classifieur#
Pour le jeu Wine Quality Data Set, on essaye de prédire la note de l’expert qui est discrète et qui va de 1 à 9. On utilise l’exemple présent à la page Decisions Trees et un autre arbre de décision appris en faisant du boosting avec AdaBoostClassifier.
from sklearn import tree
clf1 = tree.DecisionTreeClassifier(min_samples_leaf=10, min_samples_split=10)
clf1.fit(x_train, y_train)
DecisionTreeClassifier(class_weight=None, criterion='gini', max_depth=None,
max_features=None, max_leaf_nodes=None,
min_impurity_split=1e-07, min_samples_leaf=10,
min_samples_split=10, min_weight_fraction_leaf=0.0,
presort=False, random_state=None, splitter='best')
from sklearn.ensemble import AdaBoostClassifier
clf2 = AdaBoostClassifier(clf1,
algorithm='SAMME',
n_estimators=800,
learning_rate=0.5)
clf2.fit(x_train, y_train)
AdaBoostClassifier(algorithm='SAMME',
base_estimator=DecisionTreeClassifier(class_weight=None, criterion='gini', max_depth=None,
max_features=None, max_leaf_nodes=None,
min_impurity_split=1e-07, min_samples_leaf=10,
min_samples_split=10, min_weight_fraction_leaf=0.0,
presort=False, random_state=None, splitter='best'),
learning_rate=0.5, n_estimators=800, random_state=None)
On a besoin de spécifier le paramètre min_samples_leaf pour éviter de n’avoir qu’un élément dans chaque feuille de l’arbre. Ce n’est souvent pas très bon en terme de généralisation et l’arbre de décision retourne des probabilités de classification égale à 1 équivalent au ratio d’observations de la classe prédite dans cette feuille.
clf1.classes_, "nb classes", len(clf1.classes_)
(array([3, 4, 5, 6, 7, 8, 9], dtype=int64), 'nb classes', 7)
clf2.classes_, "nb classes", len(clf2.classes_)
(array([3, 4, 5, 6, 7, 8, 9], dtype=int64), 'nb classes', 7)
Il n’y a aucune note en desous de 3 ou au-dessus de 9 dans la base d’apprentissage.
matrice de confusion#
La matrice de confusion est très utilisée dans les problèmes multi-classes comme celui-ci. Elle donne une bonne indication de la pertinence du modèle. L’inconvénient est qu’elle ne tient pas compte du score retourné par le modèle.
avec la fonction confusion_matrix
from sklearn.metrics import confusion_matrix
y_pred = clf1.predict(x_test)
conf1 = confusion_matrix(y_test, y_pred)
conf1
array([[ 0, 0, 4, 6, 0, 0, 0],
[ 0, 1, 39, 32, 4, 0, 0],
[ 0, 4, 388, 239, 40, 1, 0],
[ 0, 6, 273, 586, 108, 4, 0],
[ 0, 0, 40, 166, 141, 5, 0],
[ 0, 0, 4, 27, 20, 6, 0],
[ 0, 0, 0, 0, 1, 0, 0]])
y_pred = clf2.predict(x_test)
conf2 = confusion_matrix(y_test, y_pred)
conf2
array([[ 1, 0, 5, 4, 0, 0, 0],
[ 2, 14, 44, 16, 0, 0, 0],
[ 1, 9, 495, 157, 10, 0, 0],
[ 0, 4, 200, 695, 71, 7, 0],
[ 0, 0, 4, 134, 207, 7, 0],
[ 0, 0, 0, 15, 23, 19, 0],
[ 0, 0, 0, 1, 0, 0, 0]])
On peut considérer la précision par classe : coefficient de la diagonale divissée par l’ensemble des poids de la même ligne. Ou la précision globale : somme des coefficients de la diagonale sur l’ensemble des coefficients. L’erreur correspond à 1-precision.
[ conf1[i,i] / conf1[i,:].sum() for i in range(conf1.shape [0]) ]
[0.0,
0.013157894736842105,
0.57738095238095233,
0.59979529170931423,
0.40056818181818182,
0.10526315789473684,
0.0]
sum(conf1[i,i] for i in range(conf1.shape[0])) / conf1.sum()
0.52307692307692311
Et pour l’autre classifieur :
[ conf2[i,i] / conf2[i,:].sum() for i in range(conf2.shape [0]) ]
[0.10000000000000001,
0.18421052631578946,
0.7366071428571429,
0.71136131013306036,
0.58806818181818177,
0.33333333333333331,
0.0]
sum(conf2[i,i] for i in range(conf2.shape[0])) / conf2.sum()
0.66713286713286712
courbe ROC avec decision_function#
voir plot_roc
La courbe ROC est l’outil de référence pour comparer les performances de deux classifiers en tenant compte du score de confiance qu’il retourne.
On superpose deux courbes ROC obtenue pour deux classes différentes : un vin de la classe A est bien classée si le modèle prédit A, il est mal classé s’il ne prédit pas A. Tout d’abord une courbe ROC s’appuie sur le score que retourne le classifieur avec la méthode decision_function excepté lorsque le modèle en question ne l’implémente pas. On ruse un peu pour construire un score :
y_pred = clf2.predict(x_test)
y_prob = clf2.decision_function(x_test)
y_min = y_pred.min()
import numpy
y_score = numpy.array( [y_prob[i,p-y_min] for i,p in enumerate(y_pred)] )
y_score[:5], y_pred[:5], y_prob[:5,:]
(array([ 0.44020779, 0.52681959, 0.5502509 , 0.45185157, 0.42031122]),
array([6, 5, 7, 5, 5], dtype=int64),
array([[ 0.00752588, 0.02393212, 0.09864973, 0.44020779, 0.26559545,
0.14657718, 0.01751184],
[ 0.01607109, 0.11993216, 0.52681959, 0.30492848, 0.02353611,
0.00871257, 0. ],
[ 0.00119983, 0.01753467, 0.04380276, 0.15571456, 0.5502509 ,
0.14095752, 0.09053976],
[ 0.00127399, 0.04448601, 0.45185157, 0.42330139, 0.06277742,
0.01125213, 0.0050575 ],
[ 0.05092009, 0.23678461, 0.42031122, 0.23719241, 0.04483768,
0.009954 , 0. ]]))
On crée les courbes ROC pour chacune des classes :
from sklearn.metrics import roc_curve, auc
fpr = dict()
tpr = dict()
roc_auc = dict()
nb_obs = dict()
for i in clf2.classes_:
fpr[i], tpr[i], _ = roc_curve(y_test == i, y_score)
roc_auc[i] = auc(fpr[i], tpr[i])
nb_obs[i] = (y_test == i).sum()
roc_auc, nb_obs
({3: 0.18627634660421546,
4: 0.32597746177914577,
5: 0.58229681893123852,
6: 0.474096864878507,
7: 0.4905361126603458,
8: 0.40487833568595816,
9: 0.24486940298507465},
{3: 10, 4: 76, 5: 672, 6: 977, 7: 352, 8: 57, 9: 1})
On ajoute une dernière courbe ROC pour savoir si un élément est bien classé ou pas en balayant toutes les classes :
i = "all"
fpr[i], tpr[i], _ = roc_curve(y_test == y_pred, y_score)
roc_auc[i] = auc(fpr[i], tpr[i])
nb_obs[i] = (y_test == y_pred).sum()
roc_auc_best, nb_obs_best = roc_auc, nb_obs
roc_auc, nb_obs
({3: 0.18627634660421546,
4: 0.32597746177914577,
5: 0.58229681893123852,
6: 0.474096864878507,
7: 0.4905361126603458,
8: 0.40487833568595816,
9: 0.24486940298507465,
'all': 0.74316896569948732},
{3: 10, 4: 76, 5: 672, 6: 977, 7: 352, 8: 57, 9: 1, 'all': 1431})
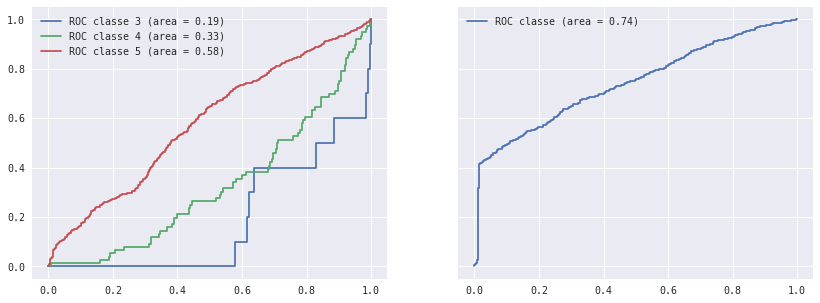
import matplotlib.pyplot as plt
fig, axes = plt.subplots(1,2, figsize=(14,5), sharey=True)
for cl in (3,4,5):
axes[0].plot(fpr[cl], tpr[cl], label='ROC classe %d (area = %0.2f)' % (cl, roc_auc[cl]))
for cl in ("all",):
axes[1].plot(fpr[cl], tpr[cl], label='ROC classe (area = %0.2f)' % (roc_auc[cl]))
axes[0].legend()
axes[1].legend()
<matplotlib.legend.Legend at 0x1c2a1481ef0>
courbe ROC avec predict_proba#
voir plot_roc, on l’applique à l’arbre de décision
y_pred = clf1.predict(x_test)
y_prob = clf1.predict_proba(x_test)
y_min = y_pred.min()
import numpy
y_score = numpy.array( [y_prob[i,p-y_min] for i,p in enumerate(y_pred)] )
y_score[:5]
array([ 0. , 0.1875 , 0.38461538, 0.08333333, 0.26666667])
On crée les courbes ROC pour chacune des classes :
from sklearn.metrics import roc_curve, auc
fpr = dict()
tpr = dict()
roc_auc = dict()
nb_obs = dict()
for i in clf1.classes_:
fpr[i], tpr[i], _ = roc_curve(y_test == i, y_score)
roc_auc[i] = auc(fpr[i], tpr[i])
nb_obs[i] = (y_test == i).sum()
roc_auc, nb_obs
({3: 0.60866510538641683,
4: 0.48463852356846682,
5: 0.4939218431771894,
6: 0.5068550111467871,
7: 0.50349766135983365,
8: 0.47187352960946427,
9: 0.23390858208955223},
{3: 10, 4: 76, 5: 672, 6: 977, 7: 352, 8: 57, 9: 1})
On ajoute une dernière courbe ROC pour savoir si un élément est bien classé ou pas :
i = "all"
fpr[i], tpr[i], _ = roc_curve(y_test == y_pred, y_score)
roc_auc[i] = auc(fpr[i], tpr[i])
nb_obs[i] = (y_test == y_pred).sum()
roc_auc, nb_obs
({3: 0.60866510538641683,
4: 0.48463852356846682,
5: 0.4939218431771894,
6: 0.5068550111467871,
7: 0.50349766135983365,
8: 0.47187352960946427,
9: 0.23390858208955223,
'all': 0.47617890131259122},
{3: 10, 4: 76, 5: 672, 6: 977, 7: 352, 8: 57, 9: 1, 'all': 1122})
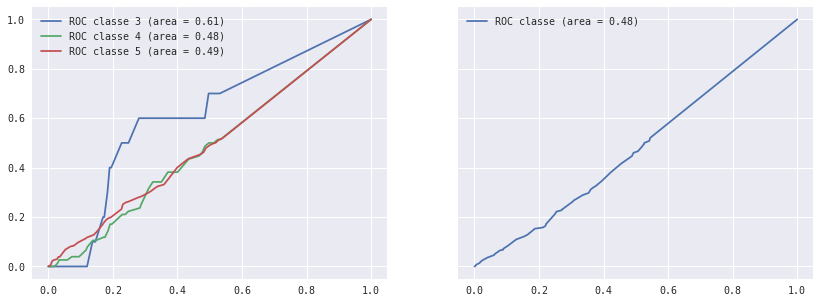
import matplotlib.pyplot as plt
fig, axes = plt.subplots(1,2, figsize=(14,5), sharey=True)
for cl in (3,4,5):
axes[0].plot(fpr[cl], tpr[cl], label='ROC classe %d (area = %0.2f)' % (cl, roc_auc[cl]))
for cl in ("all",):
axes[1].plot(fpr[cl], tpr[cl], label='ROC classe (area = %0.2f)' % (roc_auc[cl]))
axes[0].legend()
axes[1].legend()
<matplotlib.legend.Legend at 0x1c2a15a46d8>
Voir également scikit-learn for TMVA Users.
Alternatives à la courbe ROC#
un peu plus sur la courbe de ROC#
La courbe ROC est parfois difficile à interpréter. Tout d’abord, elle suppose qu’un classifieur retourne une classe et un score. Le score détermine la confiance du modèle en sa prévision. Une classifieur dessine une frontière autour de classe, plus on est loin de cette frontière, plus on est confiant. Sa confiance est proche de 1. A l’inverse, si on cherche à prédire la classe d’une observation proche de la frontière, le classifier n’est pas très confiance. Sa confiance est proche de 0.
Le coin supérieur de droit de la courbe ROC a pour coordonnées (1,1) : dans ce cas, on valide toutes les réponses du classifieur. On valide toutes ses erreurs (abscisse = 100%) et toutes ses bonnes réponses (ordonnée = 100%). Si on décide que le classifieur ne peut pas répondre pour un score < 0.5, on va rejetter un certain nombre de réponse : on fera moins d’erreurs (x=100%-40%) et moins de bonnes réponses (y=100%-10%). La courbe passera par point de coordonnées (0.6,0.9). La courbe ROC est construite en faisant varier le seuil de validation des réponses du classifieur.
from pyquickhelper.helpgen import NbImage
NbImage("roc_ex.png")
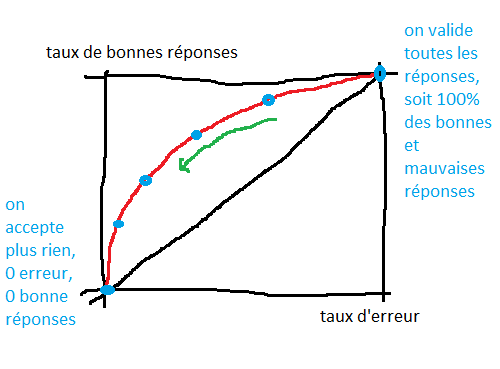
Chaque point de la courbe est obtenu pour un seuil différent. Le seuil augmente (on valide moins de réponses) dans le sens de la flèche verte. Si le score d’un classifieur est pertinent, le nombre d’erreurs baisse plus vite que le nombre de bonnes réponses. Si le score n’est pas pertinent, la courbe ROC est proche de la diagonale. Lorsque le seuil de validation augmente, le ratio erreur sur bonnes réponses ne change pas.
AUC#
L’AUC ou Area Under the
Curve
est l’aire sous la courbe ROC. Pour un classifieur binaire, si elle est
égale à 0.5, cela signifie que le score classifieur ne donne aucune
indication sur la qualité de la réponse (il est aléatoire). En-dessous,
il y a probablement une erreur. L’AUC vérifie une autre propriété. Soit
le score le score d’une bonne réponse et
le score d’une mauvaise réponse, alors :
Autrement dit, la probabilité que le score d’une bonne réponse soit supérieure au score d’une mauvaise réponse est égale à l’AUC (démonstration).
distribution des scores#
Pour illustrer cette AUC de façon différente, on peut tracer la distribution des scores pour les bonnes et les mauvaises réponses.
from sklearn.ensemble import AdaBoostClassifier
clft = tree.DecisionTreeClassifier(min_samples_leaf=10, min_samples_split=10)
clfD = AdaBoostClassifier(clft,
algorithm='SAMME',
n_estimators=800,
learning_rate=0.5)
clfD.fit(x_train, y_train)
AdaBoostClassifier(algorithm='SAMME',
base_estimator=DecisionTreeClassifier(class_weight=None, criterion='gini', max_depth=None,
max_features=None, max_leaf_nodes=None,
min_impurity_split=1e-07, min_samples_leaf=10,
min_samples_split=10, min_weight_fraction_leaf=0.0,
presort=False, random_state=None, splitter='best'),
learning_rate=0.5, n_estimators=800, random_state=None)
from sklearn.metrics import auc, precision_recall_curve
y_predD = clfD.predict(x_test)
y_probD = clfD.predict_proba(x_test)
y_testn = y_test.values
y_minD = y_predD.min()
import numpy
y_scoreD = numpy.array( [y_probD[i,p-y_minD] for i,p in enumerate(y_predD)] )
y_scoreD[:5]
array([ 0.15033537, 0.15240404, 0.15203339, 0.15100054, 0.15022789])
positive_scores = y_scoreD[y_testn == y_predD]
negative_scores = y_scoreD[y_testn != y_predD]
positive_scores.shape, negative_scores.shape
((1426,), (719,))
from sklearn.metrics import roc_curve, auc
fpr = dict()
tpr = dict()
roc_auc = dict()
nb_obs = dict()
for i in clfD.classes_:
fpr[i], tpr[i], _ = roc_curve(y_test == i, y_score)
roc_auc[i] = auc(fpr[i], tpr[i])
nb_obs[i] = (y_test == i).sum()
roc_auc, nb_obs
({3: 0.60866510538641683,
4: 0.48463852356846682,
5: 0.4939218431771894,
6: 0.5068550111467871,
7: 0.50349766135983365,
8: 0.47187352960946427,
9: 0.23390858208955223},
{3: 10, 4: 76, 5: 672, 6: 977, 7: 352, 8: 57, 9: 1})
import seaborn
ax = seaborn.distplot(positive_scores, rug=True, hist=True, label="+")
seaborn.distplot(negative_scores, rug=True, hist=True, ax=ax, label="-")
ax.legend()
<matplotlib.legend.Legend at 0x1c2a17390b8>
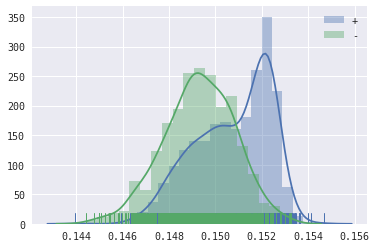
Le score de ce modèle n’est pas des plus discriminants puisqu’il existe une aire commune assez importante.
taux de rappel et précision#
Les taux de rappel et de précision (precision recall) sont très utilisés en classification. Pour un seuil donné, la précision mesure le taux de réponse parmi les réponses validées (donc ayant un score au-dessus du seuil choisi), le taux de rappel mesure le taux de réponse validées.
La dénomination vrai positif, faux positif, … est assez
trompeuse. Comme le classifieur retourne un score de confiance, on
décide de valider ou de rejeter sa réponse si le score est supérieur ou
inférieur à ce seuil :
si score >= seuil, on valide la réponse, qui est soit bonne (TP : True Positive), soit fausse (FP : False Positive)
si score < seuil, on rejete la réponse qui est soit bonne (FN : False Negative) soit fausse (TN : True Negative)
La présicion est définie comme étant le nombre de réponses justes sur le nombre de réponses validées :
et
On utilise la fonction precision_recall_curve.
from sklearn.ensemble import AdaBoostClassifier
clft = tree.DecisionTreeClassifier(min_samples_leaf=10, min_samples_split=10)
clf4 = AdaBoostClassifier(clft,
algorithm='SAMME',
n_estimators=800,
learning_rate=0.5)
clf4.fit(x_train, y_train)
AdaBoostClassifier(algorithm='SAMME',
base_estimator=DecisionTreeClassifier(class_weight=None, criterion='gini', max_depth=None,
max_features=None, max_leaf_nodes=None,
min_impurity_split=1e-07, min_samples_leaf=10,
min_samples_split=10, min_weight_fraction_leaf=0.0,
presort=False, random_state=None, splitter='best'),
learning_rate=0.5, n_estimators=800, random_state=None)
from sklearn.metrics import auc, precision_recall_curve
y_pred4 = clf4.predict(x_test)
y_prob4 = clf4.predict_proba(x_test)
y_min4 = y_pred4.min()
import numpy
y_score4 = numpy.array( [y_prob4[i,p-y_min4] for i,p in enumerate(y_pred4)] )
y_score4[:5]
precision = dict()
recall = dict()
threshold = dict()
nb_obs = dict()
for i in clf4.classes_:
precision[i], recall[i], threshold[i] = precision_recall_curve(y_test == i, y_score4)
nb_obs[i] = (y_test == i).sum()
i = "all"
precision[i], recall[i], threshold[i] = precision_recall_curve(y_test == y_pred4, y_score4)
nb_obs[i] = (y_test == y_pred4).sum()
import matplotlib.pyplot as plt
fig, axes = plt.subplots(1,2, figsize=(14,5))
for cl in (3,4,5,6,7,'all'):
axes[0].plot(precision[cl], recall[cl], label='Precision/Rappel classe %s' % str(cl))
cl = 'all'
axes[1].plot(threshold[cl], recall[cl][1:], label='recall - all')
axes[1].plot(threshold[cl], precision[cl][1:], label='precision - all')
axes[1].set_xlabel("threshold")
axes[0].set_xlabel("precision")
axes[0].set_ylabel("recall")
axes[0].legend()
axes[1].legend()
<matplotlib.legend.Legend at 0x1c2a917b5c0>
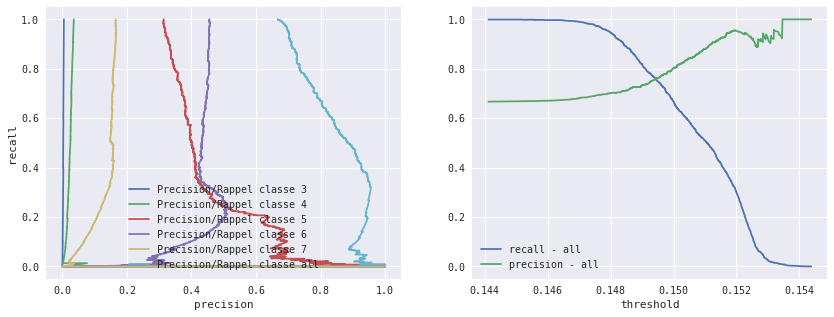
Il paraît difficile de faire montrer la précision dans baisser beaucoup le rappel. Cette courbe est inconsistance lorsque le rappel est très bas car la précision est estimée sur peu d’observations.
Régression#
from sklearn import linear_model
clr1 = linear_model.LinearRegression()
clr1.fit(x_train, y_train)
LinearRegression(copy_X=True, fit_intercept=True, n_jobs=1, normalize=False)
from sklearn import tree
clr2 = tree.DecisionTreeRegressor(min_samples_leaf=10)
clr2.fit(x_train, y_train)
DecisionTreeRegressor(criterion='mse', max_depth=None, max_features=None,
max_leaf_nodes=None, min_impurity_split=1e-07,
min_samples_leaf=10, min_samples_split=2,
min_weight_fraction_leaf=0.0, presort=False, random_state=None,
splitter='best')
cross validation#
from sklearn.model_selection import cross_val_score
cross_val_score(clr1, x_train, y_train, cv=10)
array([ 0.29336767, 0.31460783, 0.3111648 , 0.30226155, 0.28286758,
0.33354088, 0.28893078, 0.21155669, 0.29534698, 0.36294567])
cross_val_score(clr2, x_train, y_train, cv=10)
array([ 0.21747163, 0.22036389, 0.29680267, 0.26590652, 0.2008413 ,
0.28262787, 0.28729162, 0.18225887, 0.21128614, 0.30394904])
réprésentation des erreurs#
Difficile de représentation des erreurs lorsque le problème est à plusieurs dimensions. On trie les erreurs de façon croissante.
y_pred = clr1.predict(x_test)
diff1 = (y_test * 1.0 - y_pred).sort_values()
diff1.head()
4745 -3.862356
3307 -3.577666
740 -3.338887
3087 -2.784958
652 -2.782309
Name: quality, dtype: float64
y_pred = clr2.predict(x_test)
diff2 = (y_test * 1.0 - y_pred).sort_values()
diff2.head()
2050 -3.600000
3087 -2.800000
2159 -2.727273
1505 -2.700000
2225 -2.500000
Name: quality, dtype: float64
import matplotlib.pyplot as plt
fig, axes = plt.subplots(1,1, figsize=(16,4))
axes.plot(list(range(len(diff1))), list(diff1),"r-", markersize = 3, label="linear")
axes.plot(list(range(len(diff2))), list(diff2),"g-", markersize = 3, label="tree")
axes.plot(list(range(len(diff1))), [0 for i in range(len(diff1))], "b--")
axes.legend()
<matplotlib.legend.Legend at 0x1c2a93c4780>
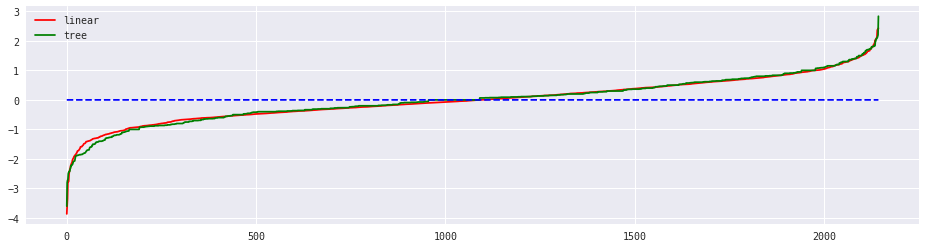
L’erreur est reliée à l’aire sous la courbe.
régression 1d et tendance#
x_train1d = x_train.copy()
x_train1d["const"] = 1.0
train_1d = x_train1d[["alcohol","const", "residual sugar"]]
train_1d.head()
| alcohol | const | residual sugar | |
|---|---|---|---|
| 101 | 9.4 | 1.0 | 9.6 |
| 3600 | 9.9 | 1.0 | 12.9 |
| 1741 | 12.9 | 1.0 | 2.0 |
| 86 | 9.9 | 1.0 | 1.9 |
| 3988 | 11.4 | 1.0 | 1.6 |
from sklearn import linear_model
clr = linear_model.LinearRegression()
clr.fit(train_1d[["const", "alcohol"]], train_1d["residual sugar"])
LinearRegression(copy_X=True, fit_intercept=True, n_jobs=1, normalize=False)
pred = clr.predict(train_1d[["const", "alcohol"]])
graph = train_1d.copy()
graph["trend"] = pred
graph.head()
| alcohol | const | residual sugar | trend | |
|---|---|---|---|---|
| 101 | 9.4 | 1.0 | 9.6 | 7.019617 |
| 3600 | 9.9 | 1.0 | 12.9 | 6.301488 |
| 1741 | 12.9 | 1.0 | 2.0 | 1.992719 |
| 86 | 9.9 | 1.0 | 1.9 | 6.301488 |
| 3988 | 11.4 | 1.0 | 1.6 | 4.147104 |
ax = graph.plot(x="alcohol", y="residual sugar", kind="scatter", label="residual sugar")
graph.sort_values("alcohol").plot(x="alcohol", y="trend", ax=ax, color="green", label="trend")
<matplotlib.axes._subplots.AxesSubplot at 0x1c2a928c208>
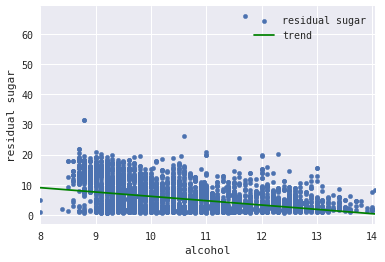
On peut aussi jouer avec la fonction add_trend de statsmodels.
Exercice 1 : créer une fonction pour automatiser la création de ce graphe#
Autres variantes#
On agrège les classes 8 et 9, 3 et 4#
On agrége ces classes pour lesquels on manque d’observations.
y_train89 = y_train.copy()
y_test89 = y_test.copy()
y_train89[y_train89==9] = 8
y_test89[y_test89==9] = 8
y_train89[y_train89==3] = 4
y_test89[y_test89==3] = 4
from sklearn.ensemble import AdaBoostClassifier
clft = tree.DecisionTreeClassifier(min_samples_leaf=10, min_samples_split=10)
clf89 = AdaBoostClassifier(clft,
algorithm='SAMME',
n_estimators=800,
learning_rate=0.5)
clf89.fit(x_train, y_train89)
AdaBoostClassifier(algorithm='SAMME',
base_estimator=DecisionTreeClassifier(class_weight=None, criterion='gini', max_depth=None,
max_features=None, max_leaf_nodes=None,
min_impurity_split=1e-07, min_samples_leaf=10,
min_samples_split=10, min_weight_fraction_leaf=0.0,
presort=False, random_state=None, splitter='best'),
learning_rate=0.5, n_estimators=800, random_state=None)
from sklearn.metrics import confusion_matrix
y_pred = clf89.predict(x_test)
conf89 = confusion_matrix(y_test89, y_pred)
conf89
array([[ 18, 48, 20, 0, 0],
[ 11, 497, 154, 9, 1],
[ 6, 197, 696, 71, 7],
[ 0, 1, 142, 203, 6],
[ 0, 0, 17, 22, 19]])
from sklearn.metrics import roc_curve, auc
y_pred89 = clf89.predict(x_test)
y_prob89 = clf89.predict_proba(x_test)
y_min89 = y_pred89.min()
import numpy
y_score89 = numpy.array( [y_prob89[i,p-y_min89] for i,p in enumerate(y_pred89)] )
y_score89[:5]
fpr89 = dict()
tpr89 = dict()
roc_auc89 = dict()
nb_obs89 = dict()
for i in clf89.classes_:
fpr89[i], tpr89[i], _ = roc_curve(y_test89 == i, y_score89)
roc_auc89[i] = auc(fpr89[i], tpr89[i])
nb_obs89[i] = (y_test89 == i).sum()
i = "all"
fpr89[i], tpr89[i], _ = roc_curve(y_test89 == y_pred89, y_score89)
roc_auc89[i] = auc(fpr89[i], tpr89[i])
nb_obs89[i] = (y_test89 == y_pred89).sum()
roc_auc89, nb_obs89
({4: 0.30029818042174455,
5: 0.62440395370639767,
6: 0.47944504423662038,
7: 0.43140622623333164,
8: 0.32624787270954847,
'all': 0.72995875706657676},
{4: 86, 5: 672, 6: 977, 7: 352, 8: 58, 'all': 1433})
A comparer avec le meilleur classifieur :
roc_auc_best, nb_obs_best
({3: 0.18627634660421546,
4: 0.32597746177914577,
5: 0.58229681893123852,
6: 0.474096864878507,
7: 0.4905361126603458,
8: 0.40487833568595816,
9: 0.24486940298507465,
'all': 0.74316896569948732},
{3: 10, 4: 76, 5: 672, 6: 977, 7: 352, 8: 57, 9: 1, 'all': 1431})
import matplotlib.pyplot as plt
fig, axes = plt.subplots(1,2, figsize=(14,5), sharey=True)
for cl in (4,5,6,7,8):
axes[0].plot(fpr89[cl], tpr89[cl], label='ROC classe %d (area = %0.2f)' % (cl, roc_auc89[cl]))
for cl in ("all",):
axes[1].plot(fpr89[cl], tpr89[cl], label='ROC classe (area = %0.2f)' % (roc_auc89[cl]))
axes[0].legend()
axes[1].legend()
<matplotlib.legend.Legend at 0x1c2ae435dd8>
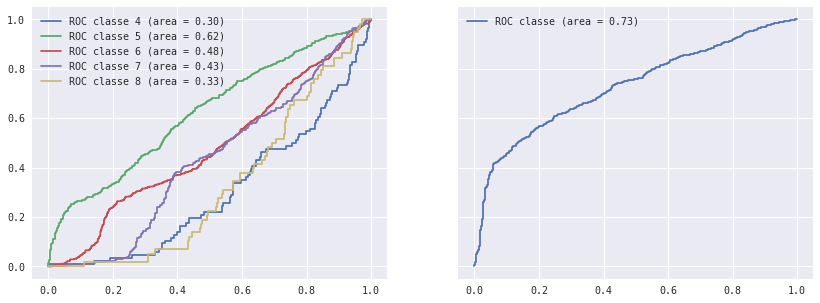
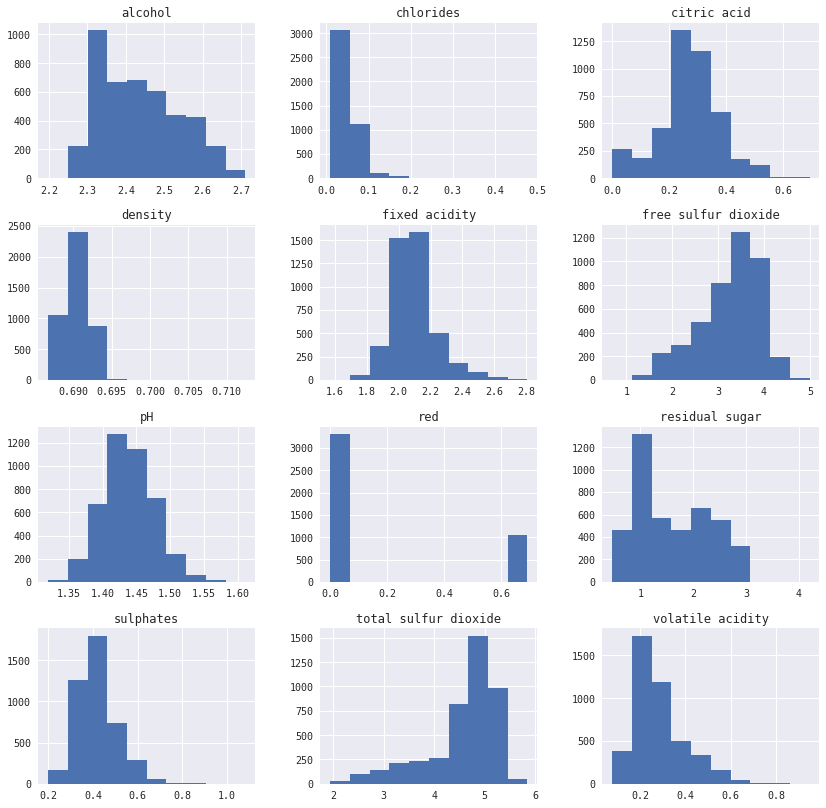
On normalise les features#
Même si cette méthode n’apporte pas grand chose dans ce cas, la normalisation par logarithme aide le classifieur lorsque les distributions ont des queues épaisses ou des points aberrants : cela donne moins d’importance aux événements extrêmes.
import math
x_train_n = x_train.copy()
x_test_n = x_test.copy()
x_train_n = x_train_n.applymap(lambda x: math.log(1+x))
x_test_n = x_test_n.applymap(lambda x: math.log(1+x))
x_train_n.hist(figsize=(14,14))
array([[<matplotlib.axes._subplots.AxesSubplot object at 0x000001C2A929A080>,
<matplotlib.axes._subplots.AxesSubplot object at 0x000001C2B2579470>,
<matplotlib.axes._subplots.AxesSubplot object at 0x000001C2B26BFF28>],
[<matplotlib.axes._subplots.AxesSubplot object at 0x000001C2B263ABA8>,
<matplotlib.axes._subplots.AxesSubplot object at 0x000001C2B270D390>,
<matplotlib.axes._subplots.AxesSubplot object at 0x000001C2B270D3C8>],
[<matplotlib.axes._subplots.AxesSubplot object at 0x000001C2B27EA5F8>,
<matplotlib.axes._subplots.AxesSubplot object at 0x000001C2B2823F28>,
<matplotlib.axes._subplots.AxesSubplot object at 0x000001C2B28B3BA8>],
[<matplotlib.axes._subplots.AxesSubplot object at 0x000001C2B28C24E0>,
<matplotlib.axes._subplots.AxesSubplot object at 0x000001C2B2980668>,
<matplotlib.axes._subplots.AxesSubplot object at 0x000001C2B29E2390>]], dtype=object)
from sklearn.ensemble import AdaBoostClassifier
clft = tree.DecisionTreeClassifier(min_samples_leaf=10, min_samples_split=10)
clfn = AdaBoostClassifier(clft,
algorithm='SAMME',
n_estimators=800,
learning_rate=0.5)
clfn.fit(x_train_n, y_train)
AdaBoostClassifier(algorithm='SAMME',
base_estimator=DecisionTreeClassifier(class_weight=None, criterion='gini', max_depth=None,
max_features=None, max_leaf_nodes=None,
min_impurity_split=1e-07, min_samples_leaf=10,
min_samples_split=10, min_weight_fraction_leaf=0.0,
presort=False, random_state=None, splitter='best'),
learning_rate=0.5, n_estimators=800, random_state=None)
from sklearn.metrics import confusion_matrix
y_predn = clfn.predict(x_test_n)
confn = confusion_matrix(y_test, y_predn)
confn
array([[ 1, 0, 5, 4, 0, 0, 0],
[ 2, 15, 44, 15, 0, 0, 0],
[ 1, 8, 496, 154, 12, 1, 0],
[ 0, 3, 209, 689, 71, 5, 0],
[ 0, 0, 3, 138, 204, 7, 0],
[ 0, 0, 0, 15, 23, 19, 0],
[ 0, 0, 0, 1, 0, 0, 0]])
from sklearn.metrics import roc_curve, auc
y_predn = clfn.predict(x_test_n)
y_probn = clfn.predict_proba(x_test_n)
y_minn = y_predn.min()
import numpy
y_scoren = numpy.array( [y_probn[i,p-y_minn] for i,p in enumerate(y_predn)] )
y_scoren[:5]
fpr = dict()
tpr = dict()
roc_auc = dict()
nb_obs = dict()
for i in clfn.classes_:
fpr[i], tpr[i], _ = roc_curve(y_test == i, y_scoren)
roc_auc[i] = auc(fpr[i], tpr[i])
nb_obs[i] = (y_test == i).sum()
i = "all"
fpr[i], tpr[i], _ = roc_curve(y_test == y_predn, y_scoren)
roc_auc[i] = auc(fpr[i], tpr[i])
nb_obs[i] = (y_test == y_predn).sum()
roc_auc, nb_obs
({3: 0.2359718969555035,
4: 0.31540790109638522,
5: 0.61887082565544893,
6: 0.48044317241766094,
7: 0.43716568219844854,
8: 0.32746017342206085,
9: 0.27005597014925375,
'all': 0.73407135844410853},
{3: 10, 4: 76, 5: 672, 6: 977, 7: 352, 8: 57, 9: 1, 'all': 1424})
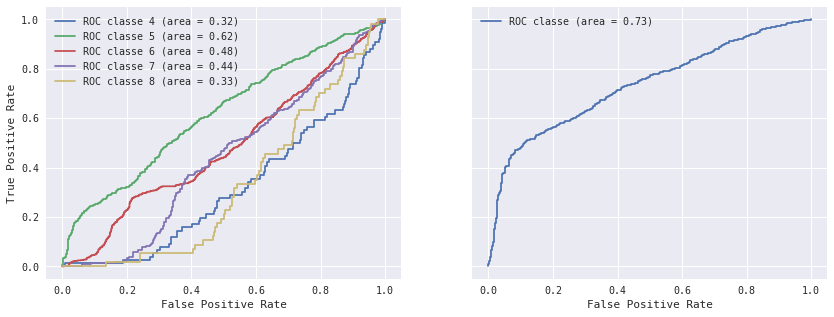
import matplotlib.pyplot as plt
fig, axes = plt.subplots(1,2, figsize=(14,5), sharey=True)
for cl in (4,5,6,7,8):
axes[0].plot(fpr[cl], tpr[cl], label='ROC classe %d (area = %0.2f)' % (cl, roc_auc[cl]))
for cl in ("all",):
axes[1].plot(fpr[cl], tpr[cl], label='ROC classe (area = %0.2f)' % (roc_auc[cl]))
axes[0].legend()
axes[1].legend()
axes[0].set_ylabel("True Positive Rate")
axes[0].set_xlabel("False Positive Rate")
axes[1].set_xlabel("False Positive Rate")
<matplotlib.text.Text at 0x1c2b2cfe860>
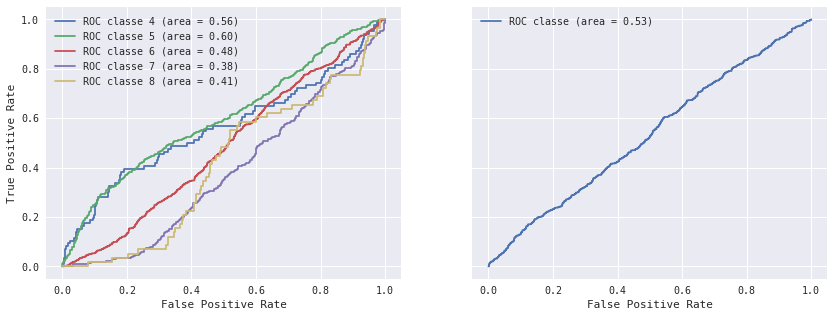
Classifieur pour les classes 8-9#
from sklearn.naive_bayes import GaussianNB
clfs89 = GaussianNB()
clfs89.fit(x_train, y_train89)
GaussianNB(priors=None)
from sklearn.metrics import confusion_matrix
y_pred89 = clfs89.predict(x_test)
confs89 = confusion_matrix(y_test89, y_pred89)
confs89
array([[ 15, 39, 26, 6, 0],
[ 35, 353, 244, 40, 0],
[ 27, 289, 416, 239, 6],
[ 6, 31, 122, 174, 19],
[ 0, 4, 15, 30, 9]])
from sklearn.metrics import roc_curve, auc
y_preds89 = clfs89.predict(x_test)
y_probs89 = clfs89.predict_proba(x_test)
y_mins89 = y_preds89.min()
import numpy
y_scores89 = numpy.array( [y_probs89[i,p-y_mins89] for i,p in enumerate(y_preds89)] )
y_scores89[:5]
fpr = dict()
tpr = dict()
roc_auc = dict()
nb_obs = dict()
for i in clfs89.classes_:
fpr[i], tpr[i], _ = roc_curve(y_test89 == i, y_scores89)
roc_auc[i] = auc(fpr[i], tpr[i])
nb_obs[i] = (y_test89 == i).sum()
i = "all"
fpr[i], tpr[i], _ = roc_curve(y_test89 == y_preds89, y_scores89)
roc_auc[i] = auc(fpr[i], tpr[i])
nb_obs[i] = (y_test89 == y_preds89).sum()
roc_auc, nb_obs
({4: 0.56018387792674251,
5: 0.59860323117706016,
6: 0.48064735491650434,
7: 0.38087670486234343,
8: 0.4091832856930423,
'all': 0.5304338589409775},
{4: 86, 5: 672, 6: 977, 7: 352, 8: 58, 'all': 967})
%matplotlib inline
import matplotlib.pyplot as plt
fig, axes = plt.subplots(1,2, figsize=(14,5), sharey=True)
for cl in clfs89.classes_:
axes[0].plot(fpr[cl], tpr[cl], label='ROC classe %d (area = %0.2f)' % (cl, roc_auc[cl]))
for cl in ("all",):
axes[1].plot(fpr[cl], tpr[cl], label='ROC classe (area = %0.2f)' % (roc_auc[cl]))
axes[0].legend()
axes[1].legend()
axes[0].set_ylabel("True Positive Rate")
axes[0].set_xlabel("False Positive Rate")
axes[1].set_xlabel("False Positive Rate")
<matplotlib.text.Text at 0x1c2b2e4eef0>
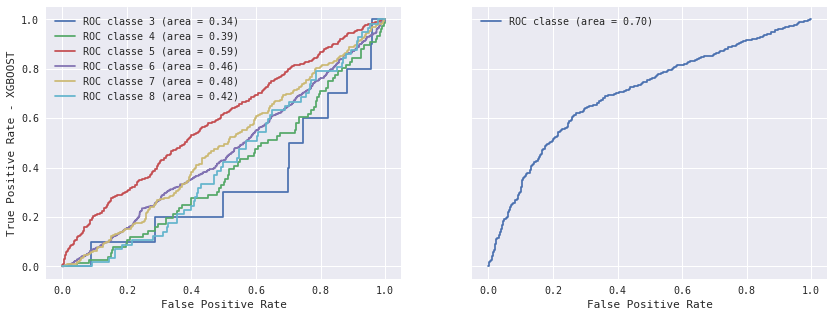
Autres modules#
XGBoost#
Le module XGBoost est utilisé dans la plupart des compétitions Kaggle.
import xgboost
c:Python36_x64libsite-packagessklearncross_validation.py:44: DeprecationWarning: This module was deprecated in version 0.18 in favor of the model_selection module into which all the refactored classes and functions are moved. Also note that the interface of the new CV iterators are different from that of this module. This module will be removed in 0.20. "This module will be removed in 0.20.", DeprecationWarning)
try:
clxg = xgboost.XGBClassifier(max_depth=10, min_child_weight=5, nthread=3, n_estimators=800,
colsample_bytree=0.5)
except Exception:
# Newer version of XGBoost have different parameters.
clxg = xgboost.XGBClassifier(max_depth=10, min_child_weight=5, nthread=3, n_estimators=800,
colsample_bytree=2)
clxg.fit(x_train, y_train)
XGBClassifier(base_score=0.5, colsample_bylevel=1, colsample_bytree=0.5,
gamma=0, learning_rate=0.1, max_delta_step=0, max_depth=10,
min_child_weight=5, missing=None, n_estimators=800, nthread=3,
objective='multi:softprob', reg_alpha=0, reg_lambda=1,
scale_pos_weight=1, seed=0, silent=True, subsample=1)
from sklearn.metrics import confusion_matrix
y_pred = clxg.predict(x_test)
confxg = confusion_matrix(y_test, y_pred)
confxg
array([[ 0, 0, 4, 6, 0, 0, 0],
[ 1, 18, 42, 15, 0, 0, 0],
[ 2, 6, 479, 172, 13, 0, 0],
[ 1, 6, 191, 697, 79, 3, 0],
[ 0, 0, 6, 138, 202, 6, 0],
[ 0, 0, 0, 21, 17, 19, 0],
[ 0, 0, 0, 1, 0, 0, 0]])
from sklearn.metrics import roc_curve, auc
y_predxg = clxg.predict(x_test)
y_probxg = clxg.predict_proba(x_test)
y_minxg = y_predxg.min()
import numpy
y_scorexg = numpy.array( [y_probxg[i,p-y_minxg] for i,p in enumerate(y_predxg)] )
y_scorexg[:5]
fpr = dict()
tpr = dict()
roc_auc = dict()
nb_obs = dict()
for i in clxg.classes_:
fpr[i], tpr[i], _ = roc_curve(y_test == i, y_scorexg)
roc_auc[i] = auc(fpr[i], tpr[i])
nb_obs[i] = (y_test == i).sum()
i = "all"
fpr[i], tpr[i], _ = roc_curve(y_test == y_predxg, y_scorexg)
roc_auc[i] = auc(fpr[i], tpr[i])
nb_obs[i] = (y_test == y_predxg).sum()
roc_auc, nb_obs
({3: 0.33550351288056207,
4: 0.39011981379257715,
5: 0.58805018103643358,
6: 0.46074876263653058,
7: 0.48162361202656789,
8: 0.42054849768098407,
9: 0.25652985074626866,
'all': 0.70095454765477516},
{3: 10, 4: 76, 5: 672, 6: 977, 7: 352, 8: 57, 9: 1, 'all': 1415})
import matplotlib.pyplot as plt
fig, axes = plt.subplots(1,2, figsize=(14,5), sharey=True)
for cl in (3,4,5,6,7,8):
axes[0].plot(fpr[cl], tpr[cl], label='ROC classe %d (area = %0.2f)' % (cl, roc_auc[cl]))
for cl in ("all",):
axes[1].plot(fpr[cl], tpr[cl], label='ROC classe (area = %0.2f)' % (roc_auc[cl]))
axes[0].legend()
axes[1].legend()
axes[0].set_ylabel("True Positive Rate - XGBOOST")
axes[0].set_xlabel("False Positive Rate")
axes[1].set_xlabel("False Positive Rate")
<matplotlib.text.Text at 0x1c2b85d0780>
LightGBM#
Le module LightGBM est un équivalent open source écrit par Microsoft. Il est plus rapide que XGBoost dans la plupart des cas.
import lightgbm
clgbm = lightgbm.LGBMClassifier(max_depth=10, min_child_weight=5, nthread=3, n_estimators=800,
colsample_bytree=0.5)
clgbm.fit(x_train, y_train)
LGBMClassifier(boosting_type='gbdt', colsample_bytree=0.5, learning_rate=0.1,
max_bin=255, max_depth=10, min_child_samples=10,
min_child_weight=5, min_split_gain=0, n_estimators=800, nthread=3,
num_leaves=31, objective='multiclass', reg_alpha=0, reg_lambda=0,
seed=0, silent=True, subsample=1, subsample_for_bin=50000,
subsample_freq=1)
from sklearn.metrics import confusion_matrix
y_pred = clgbm.predict(x_test)
confgbm = confusion_matrix(y_test, y_pred)
confgbm
array([[ 0, 0, 4, 6, 0, 0, 0],
[ 2, 16, 44, 14, 0, 0, 0],
[ 2, 6, 479, 172, 13, 0, 0],
[ 0, 6, 191, 692, 84, 4, 0],
[ 0, 0, 10, 138, 200, 4, 0],
[ 0, 0, 0, 19, 19, 19, 0],
[ 0, 0, 0, 1, 0, 0, 0]])
from sklearn.metrics import roc_curve, auc
y_predgbm = clgbm.predict(x_test)
y_probgbm = clgbm.predict_proba(x_test)
y_mingbm = y_predgbm.min()
import numpy
y_scoregbm = numpy.array( [y_probgbm[i,p-y_minxg] for i,p in enumerate(y_predgbm)] )
y_scoregbm[:5]
fpr = dict()
tpr = dict()
roc_auc = dict()
nb_obs = dict()
for i in clxg.classes_:
fpr[i], tpr[i], _ = roc_curve(y_test == i, y_scorexg)
roc_auc[i] = auc(fpr[i], tpr[i])
nb_obs[i] = (y_test == i).sum()
i = "all"
fpr[i], tpr[i], _ = roc_curve(y_test == y_predxg, y_scorexg)
roc_auc[i] = auc(fpr[i], tpr[i])
nb_obs[i] = (y_test == y_predxg).sum()
roc_auc, nb_obs
({3: 0.33550351288056207,
4: 0.39011981379257715,
5: 0.58805018103643358,
6: 0.46074876263653058,
7: 0.48162361202656789,
8: 0.42054849768098407,
9: 0.25652985074626866,
'all': 0.70095454765477516},
{3: 10, 4: 76, 5: 672, 6: 977, 7: 352, 8: 57, 9: 1, 'all': 1415})
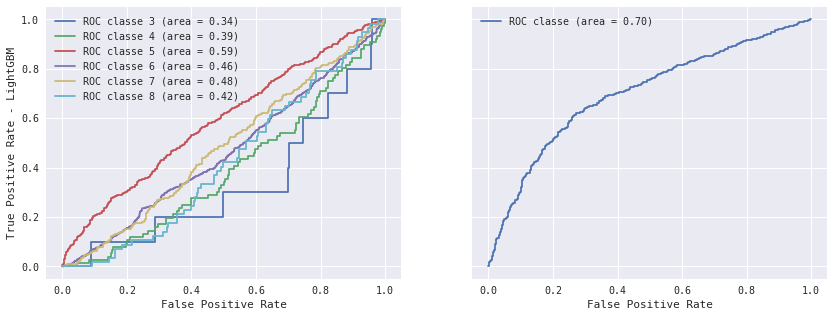
import matplotlib.pyplot as plt
fig, axes = plt.subplots(1,2, figsize=(14,5), sharey=True)
for cl in (3,4,5,6,7,8):
axes[0].plot(fpr[cl], tpr[cl], label='ROC classe %d (area = %0.2f)' % (cl, roc_auc[cl]))
for cl in ("all",):
axes[1].plot(fpr[cl], tpr[cl], label='ROC classe (area = %0.2f)' % (roc_auc[cl]))
axes[0].legend()
axes[1].legend()
axes[0].set_ylabel("True Positive Rate - LightGBM")
axes[0].set_xlabel("False Positive Rate")
axes[1].set_xlabel("False Positive Rate")
<matplotlib.text.Text at 0x1c2b9866588>
Exercice 2 : simplifier l’apprentissage de chaque modèle#
Exercice 3 : grid_search#
Considérer un modèle et estimer au mieux ses paramètres.