Simulation d’une corde qui chute

La corde chute jusqu’à sa stabilisation autour d’une position d’équilibre. L’étude physique est détaillée dans le document. La corde est représentée par une suite de n masses ponctuelles reliées par des ressorts de masse nulle qui exercent une traction lorsque leur longueur dépasse un certain seuil. On considère une corde de longueur L et de masse M, elle est divisée en n masses de masses \frac{M}{n}. Ces masses sont reliées par n-1 ressorts qui exercent une traction sur les masses qu’ils relient lorsque leur longueur dépasse le seuil \frac{L}{n-1}. Les masses sont initialement placées sur une droite reliant les deux extremités fixes de la corde. Chaque masse est soumis à une accélération égale à la somme de trois forces qui sont son poids et les tractions exercées par les ressorts auxquels elle est attachée

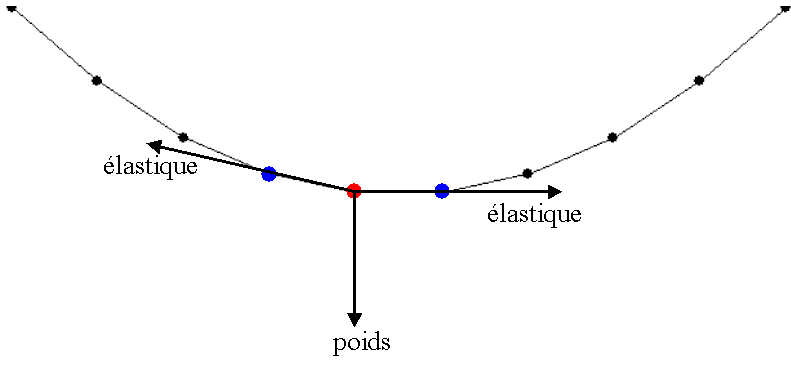
../_images/corde.png

A chaque instant t, on peut calculer cette accélération, en déduire la vitesse puis la position à l’instant t+1. Ce mécanisme permet d’obtenir une animation de la corde atteignant sa position d’équilibre.

Le même code légèrement modifié peut également simuler un pendule.

On construit l’algorithme suivant étant donné une corde de longueur L suspendue entre les points d’abscisse (-x_0,0) et (0,0) de telle sorte que 2 x_0 < L. Cette corde à une masse M et une raideur k. La pesanteur est notée g. On divise cette corde en n masses ponctuelles de masse \forall i \in [[1..n]], \; m_i = \frac{M}{n}. Chaque masse a une position p_i. On note pour chaque point p_i sa vitesse v_i. On désigne par f un coefficient de freinage, plus il est grand, plus la corde convergera rapidement vers sa position d’équilibre. dt désigne un pas de temps.

\forall i \in [[1..n]], \; p_i = -x_0 + 2x_0 \frac{i-1}{n-1}

Pour chaque masse, on calcule une accélération a_i \in \mathbb{R}^2 et a_0 = a_n = 0 (les extrémités sont fixes). On met à la jour comme suit :

  1. a_i \longleftarrow (0, - m_i g) - f v_i

  2. Si \left\Vert\overset{\longrightarrow}{p_{i-1},p_i }\right\Vert > \frac{L}{n-1} alors a_i \longleftarrow a_i + k \left[ \left\Vert\overset{\longrightarrow}{p_{i-1},p_i }\right\Vert - \frac{L}{n-1} \right] \frac{\overset{\longrightarrow}{p_{i-1},p_i }}{ \left\Vert\overset{\longrightarrow}{p_{i-1},p_i }\right\Vert }.

  3. Si \left\Vert\overset{\longrightarrow}{p_{i+1},p_i }\right\Vert > \frac{L}{n-1} alors a_i \longleftarrow a_i + k \left[ \left\Vert\overset{\longrightarrow}{p_{i+1},p_i }\right\Vert - \frac{L}{n-1} \right] \frac{\overset{\longrightarrow}{p_{i+1},p_i }}{ \left\Vert\overset{\longrightarrow}{p_{i+1},p_i }\right\Vert }.

La mise à jour des positions se fait en appliquant les lois de la mécanique :

\begin{array}{l} p_i \longleftarrow p_i + v_i dt \\ v_i \longleftarrow v_i + a_i dt \end{array}

Tant que l’algorithme n’a pas convergé, on retourne à la première étape. L’implémentation est réalisée dans le module corde.