Problème de dès et problème de flots#
Cet exposé commence par un problème issue de Google Jam: Dice Straight. On dispose de dés à six faces, sur chaque face, un nombre entier quelconque. Il faut trouver la plus grande séquence de dés qu’on peut poser sur une ligne en formant une suite de nombres entiers consécutifs. Par exemple, avec les quatre dés suivants :
4 8 15 16 23 42
8 6 7 5 30 9
1 2 3 4 55 6
2 10 18 36 54 86
Il existe une séquence de 3 dés en prenant les couples
(dé, face) : (4,2), (3,3), (1,4), (2,5).
Comment trouver la longueur de la plus grande séquence
de ce type ?
Quelques propriétés#
On peut aisément trouver des majorants pour cette séquence la plus grande :
Elle ne peut pas être plus grande que le nombre de dés.
Elle ne peut pas être plus grande que la différence qui sépare la plus petite et la plus grande face.
Si un entier n’est présent sur aucune face, la séquence la plus grande est constituée d’entiers strictement supérieurs ou strictement inférieurs.
Une piste gourmande#
On peut construire un graphe pour lequel chaque noeud est un couple (dé, face), chaque arc relie deux noeuds qui peuvent faire partie d’une séquence. Une solution consiste à trouver dans ce graphe un chemin le plus long possible qui ne passe pas deux fois par le même dé. L’image suivant représente une partie du graphe qu’on peut construire ainsi avec le problème ci-dessus.
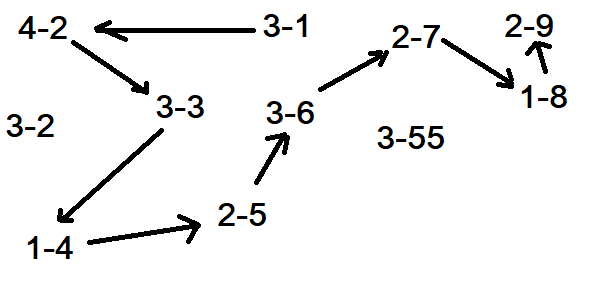
On peut facilement modifier l’algorithme de Dikjstra (plus court de chemins) pour conserver l’historique des noeuds visités mais on peut prédire que sur certains problèmes, ce nombre d’historiques va être très grand et grandir exponentiellement.
Si nous avons, six dés identiques, n’importe quelle séquence fonctionne et le nombre de chemins est aussi grand que le nombre de permutations. On peut néanmoins se contenter de conserver le nombre de noeuds distincts et non la séquence de noeuds mais la quantité d’information sera tout de même importante car il faut conserver tous les ensembles de noeuds distincts.
On peut aussi construire un graphe où chaque noeud est repéré par un triplet (position, dé, face). Le graphe a plus de noeuds que le précédent mais autant d’arcs mais cela n’apporte pas grand chose pour le moment. On peut aussi construire un graphe dans lequel chaque noeud réprésente deux dés qu’on peut placer dans une séquence. Le graphe est plus grand mais possède moins d’arcs. Mais cela a peut de chance d’aboutir.
Problème de flots#
Les solutions précédentes qui fonctionnent sur de petits graphes retournent un chemin or nous n’avons besoin que de la longueur de ce chemin. Peut-on trouver un algorithme qui lors de son optimisation tienne compte du fait qu’il ne faut pas passer deux fois par le même dé sans pour autant retenir cette information ?
Le problème du flot maximal consiste à trouver le débit maximal qu’un réseau de canalisation peut faire passer d’un point A à un point B en tenant des capacités de chaque tuyau qu’on résoud avec un algorithme de Floyd-Fulkerson ou Edmonds-Karp. Cet algorithme est utile pour ce problème si on arrive à construire un diagramme pour lequel le flot maximal indique la longueur de la plus grande séquence de dés. Etant donné qu’il n’y pas de notion de débit dans le problème de dés mais plutôt d’existence, il s’agit plus de déterminer si le flot maximal est positif ou nul.
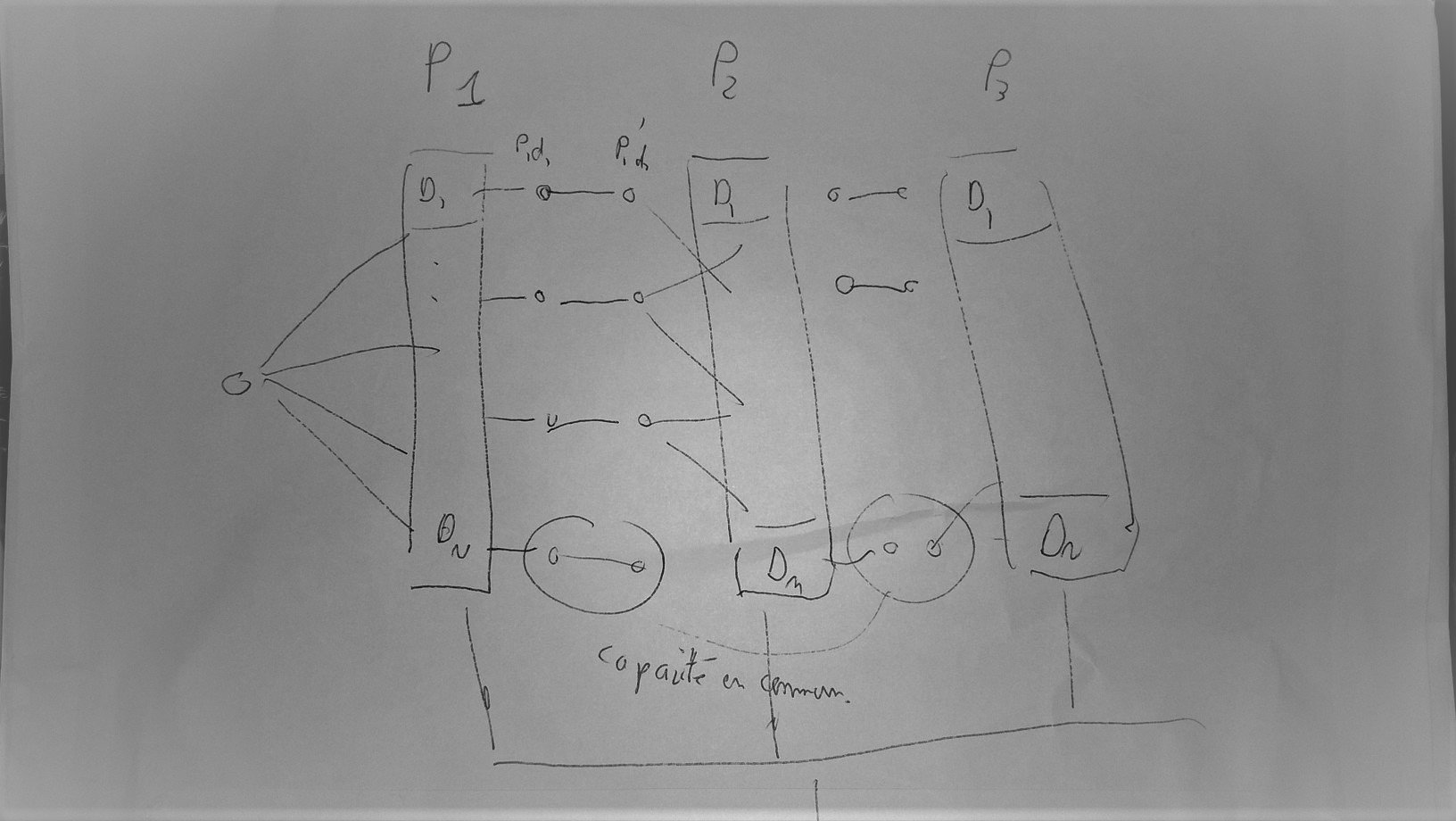
L’idée est de créer un réseau qui passe par des tuyaux dont on peut partager les capacités de sorte que s’il est emprunté à un moment, il ne le soit pas à un autre. On peut essayer de bidouiller l’algorithme original afin de tenir compte de ces coefficients partagés sans garantie toutefois que l’algorithme converge.
Une solution simple#
Cette approche consiste à trier les faces par ordre croissant. Une fois ceci fait, une séquence de dés qui vérifie les conditions initiales est un sous-ensemble de faces prises dans le même ordre.