Base d’apprentissage et de test

Links: notebook, html, PDF, python, slides, GitHub

Le modèle est estimé sur une base d’apprentissage et évalué sur une base de test.

%matplotlib inline

from papierstat.datasets import load_wines_dataset
df = load_wines_dataset()
X = df.drop(['quality', 'color'], axis=1)
y = df['quality']

On divise en base d’apprentissage et de test avec la fonction train_test_split.

from sklearn.model_selection import train_test_split
X_train, X_test, y_train, y_test = train_test_split(X, y)

from sklearn.neighbors import KNeighborsRegressor
knn = KNeighborsRegressor(n_neighbors=1)
knn.fit(X_train, y_train)

KNeighborsRegressor(algorithm='auto', leaf_size=30, metric='minkowski',
          metric_params=None, n_jobs=1, n_neighbors=1, p=2,
          weights='uniform')

prediction = knn.predict(X_test)

import pandas
res = pandas.DataFrame(dict(expected=y_test, prediction=prediction))
res.head()

	expected	prediction
2647	5	5.0
920	5	5.0
4360	5	6.0
6435	5	5.0
5436	6	6.0

from seaborn import jointplot
ax = jointplot("expected", "prediction", res, kind="kde", size=4)
ax.ax_marg_y.set_title('Distribution valeurs attendues\nvaleurs prédites');

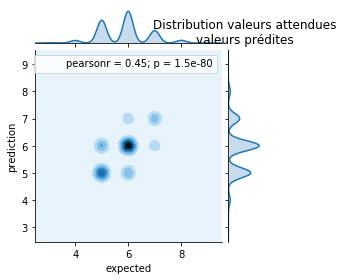
Le résultat paraît acceptable. On enlève les réponses correctes.

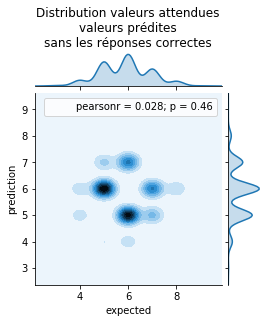
ax = jointplot("expected", "prediction", res[res['expected'] != res['prediction']], kind="kde", size=4)
ax.ax_marg_x.set_title('Distribution valeurs attendues\nvaleurs prédites\n' +
                       'sans les réponses correctes');

res['diff'] = res['prediction'] - res["expected"]

ax = res['diff'].hist(bins=15, figsize=(3,3))
ax.set_title("Répartition des différences");

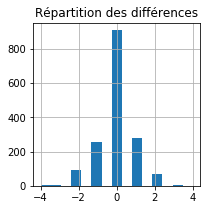
Si on fait la moyenne des erreurs en valeur absolue :

import numpy
numpy.abs(res['diff']).mean()

0.5661538461538461

Le modèle se trompe en moyenne d’un demi point. Le module scikit-learn propose de nombreuses métriques pour évaluer les résultats. On s’intéresse plus particulièrement à celle de la régression. Celle qu’on a utilisée s’appelle mean_absolute_error.

from sklearn.metrics import mean_absolute_error
mean_absolute_error(y_test, prediction)

0.5661538461538461

Un autre indicateur très utilisé : R2.

from sklearn.metrics import r2_score
r2_score(y_test, prediction)

-0.05471047787566907

Une valeur négative implique que le modèle fait moins bien que si la prédiction était constante et égale à la moyenne des notes sur la base de test. Essayons.

const = numpy.mean(y_test) * numpy.ones(y_test.shape[0])
r2_score(y_test, const)

0.0

Pour être rigoureux, il faudrait prendre la moyenne des notes sur la base d’apprentissage, celles des vins connus.

const = numpy.mean(y_train) * numpy.ones(y_test.shape[0])
r2_score(y_test, const)

-0.0027584386563039853

Sensiblement pareil et on sait maintenant que le modèle n’est pas bon. On cherche une explication. Une raison possible est que les bases d’apprentissage et de test ne sont pas homogènes : le modèle apprend sur des données et est testé sur d’autres qui n’ont rien à voir. On commence par regarder la distribution des notes.

ys = pandas.DataFrame(dict(y=y_train))
ys['base'] = 'train'
ys2 = pandas.DataFrame(dict(y=y_test))
ys2['base'] = 'test'
ys = pandas.concat([ys, ys2])
ys['compte'] = 1
piv = ys.groupby(['base', 'y'], as_index=False).count().pivot('y', 'base', 'compte')
piv['ratio'] = piv['test'] / piv['train']
piv

base	test	train	ratio
y
3	6	24	0.250000
4	57	159	0.358491
5	511	1627	0.314075
6	710	2126	0.333960
7	279	800	0.348750
8	60	133	0.451128
9	2	3	0.666667

On voit le ratio entre les deux classes est à peu près égal à 1/3 sauf pour les notes sous-représentées. On voit également que les classes 5,6,7 sont sur-représentées. Autrement dit, si je choisis un vin au hasard, il y a 90% de chance que sa note soit 5, 6 ou 7.