2A.ml - Statistiques descriptives avec scikit-learn#
Links: notebook, html, python, slides, GitHub
ACP, CAH, régression lineaire.
%matplotlib inline
import matplotlib.pyplot as plt
from jyquickhelper import add_notebook_menu
add_notebook_menu()
Introduction#
Les statistiques descriptives sont abordées de la première année à l’ENSAE. Un des livres que je consulte souvent est celui de Gilles Saporta : Probabilités, analyse des données et statistique qui est en français.
Le module scikit-learn a largement contribué au succès de Python dans le domaine du machine learning. Ce module inclut de nombreuses techniques regroupées sous le terme statistiques descriptives. La correspondance anglais-français n’est pas toujours évidente. Voici quelques termes :
scikit-learn est orienté machine learning, les résultats qu’il produit sont un peu moins complets que statsmodels pour les modèles statistiques linéaires ou fastcluster pour la CAH. L’objectif de ces deux heures est d’utiliser ces modules pour étudier un jeu de données :
ACP (Analyse en Composantes Principales)#
Le site data.gouv.fr propose de nombreux jeux de données dont Séries chronologiques Education : les élèves du second degré. Ces données sont également accessibles comme ceci :
import pandas, numpy, pyensae.datasource
from sklearn.decomposition import PCA
import matplotlib.pyplot as plt
fichier = pyensae.datasource.download_data("eleve_region.txt")
df = pandas.read_csv("eleve_region.txt", sep="\t", encoding="utf8", index_col=0)
print(df.shape)
df.head(n=5)
(27, 21)
| 1993 | 1994 | 1995 | 1996 | 1997 | 1998 | 1999 | 2000 | 2001 | 2002 | ... | 2004 | 2005 | 2006 | 2007 | 2008 | 2009 | 2010 | 2011 | 2012 | 2013 | |
|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|
| académie | |||||||||||||||||||||
| Aix-Marseille | 241357 | 242298 | 242096 | 242295 | 243660 | 244608 | 245536 | 247288 | 249331 | 250871 | ... | 250622 | 248208 | 245755 | 243832 | 242309 | 240664 | 240432 | 241336 | 239051 | 240115 |
| Amiens | 198281 | 196871 | 195709 | 194055 | 192893 | 191862 | 189636 | 185977 | 183357 | 180973 | ... | 175610 | 172110 | 168718 | 165295 | 163116 | 162548 | 163270 | 164422 | 165275 | 166345 |
| Besançon | 116373 | 115600 | 114282 | 113312 | 112076 | 110261 | 108106 | 105463 | 103336 | 102264 | ... | 100117 | 98611 | 97038 | 95779 | 95074 | 94501 | 94599 | 94745 | 94351 | 94613 |
| Bordeaux | 253551 | 252644 | 249658 | 247708 | 247499 | 245757 | 244992 | 243047 | 243592 | 245198 | ... | 244805 | 244343 | 242602 | 242933 | 243146 | 244336 | 246806 | 250626 | 252085 | 255761 |
| Caen | 145435 | 144369 | 141883 | 140658 | 139585 | 137704 | 135613 | 133255 | 131206 | 129271 | ... | 125552 | 123889 | 122550 | 121002 | 119857 | 119426 | 119184 | 119764 | 119010 | 119238 |
5 rows × 21 columns
On veut observer l’évolution du nombre d’élèves. On prend l’année 1993 comme base 100.
for c in df.columns:
if c != "1993":
df[c] /= df ["1993"]
df["1993"] /= df["1993"]
df.head()
| 1993 | 1994 | 1995 | 1996 | 1997 | 1998 | 1999 | 2000 | 2001 | 2002 | ... | 2004 | 2005 | 2006 | 2007 | 2008 | 2009 | 2010 | 2011 | 2012 | 2013 | |
|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|
| académie | |||||||||||||||||||||
| Aix-Marseille | 1.0 | 1.003899 | 1.003062 | 1.003886 | 1.009542 | 1.013470 | 1.017315 | 1.024574 | 1.033038 | 1.039419 | ... | 1.038387 | 1.028385 | 1.018222 | 1.010255 | 1.003944 | 0.997129 | 0.996168 | 0.999913 | 0.990446 | 0.994854 |
| Amiens | 1.0 | 0.992889 | 0.987029 | 0.978687 | 0.972826 | 0.967627 | 0.956400 | 0.937947 | 0.924733 | 0.912710 | ... | 0.885662 | 0.868011 | 0.850904 | 0.833640 | 0.822651 | 0.819786 | 0.823427 | 0.829237 | 0.833539 | 0.838936 |
| Besançon | 1.0 | 0.993358 | 0.982032 | 0.973697 | 0.963076 | 0.947479 | 0.928961 | 0.906250 | 0.887972 | 0.878761 | ... | 0.860311 | 0.847370 | 0.833853 | 0.823035 | 0.816976 | 0.812053 | 0.812895 | 0.814149 | 0.810764 | 0.813015 |
| Bordeaux | 1.0 | 0.996423 | 0.984646 | 0.976955 | 0.976131 | 0.969261 | 0.966243 | 0.958572 | 0.960722 | 0.967056 | ... | 0.965506 | 0.963684 | 0.956817 | 0.958123 | 0.958963 | 0.963656 | 0.973398 | 0.988464 | 0.994218 | 1.008716 |
| Caen | 1.0 | 0.992670 | 0.975577 | 0.967154 | 0.959776 | 0.946842 | 0.932465 | 0.916251 | 0.902162 | 0.888858 | ... | 0.863286 | 0.851851 | 0.842644 | 0.832001 | 0.824128 | 0.821164 | 0.819500 | 0.823488 | 0.818304 | 0.819871 |
5 rows × 21 columns
Il n’est pas évident d’analyser ce tableaux de chiffres. On utilise une ACP pour projeter les académies dans un plan.
pca = PCA(n_components=4)
print(pca.fit(df))
pca.explained_variance_ratio_
PCA(n_components=4)
array([9.63024476e-01, 3.37267932e-02, 1.93116666e-03, 6.61046399e-04])
Le premier axe explique l’essentiel de la variance. Les variables n’ont pas été normalisées car elles évoluent dans les mêmes ordres de grandeur.
plt.bar(numpy.arange(len(pca.explained_variance_ratio_)) + 0.5,
pca.explained_variance_ratio_)
plt.title("Variance expliquée");

On affiche les académies dans le plan des deux premiers axes :
X_reduced = pca.transform(df)
plt.figure(figsize=(18, 6))
plt.scatter(X_reduced[:, 0], X_reduced[:, 1])
for label, x, y in zip(df.index, X_reduced[:, 0], X_reduced[:, 1]):
plt.annotate(
label,
xy=(x, y), xytext=(-10, 10),
textcoords='offset points', ha='right', va='bottom',
bbox=dict(boxstyle='round,pad=0.5', fc='yellow', alpha=0.5),
arrowprops = dict(arrowstyle='->', connectionstyle='arc3,rad=0'))
plt.title("ACP rapprochant des profils d'évolution similaires");
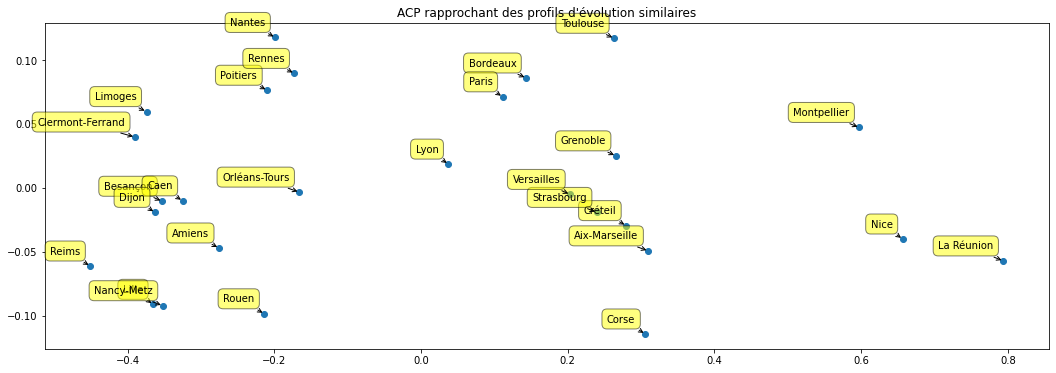
Puis on vérifie que deux villes proches ont le même profil d’évolution au cours des années :
sub = df.loc[["Paris", "Bordeaux", "Lyon", "Nice", "La Réunion", "Reims"], :]
ax = sub.transpose().plot(figsize=(10, 4))
ax.set_title("Evolution des effectifs au cours du temps");
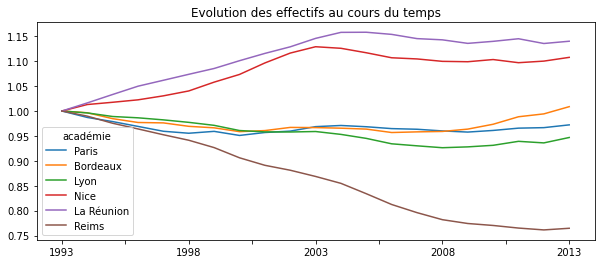
L’ACP version statsmodels produit le même type de résultats. Un exemple est disponible ici : PCA and Biplot using Python.
Exercice 1 : CAH (classification ascendante hiérarchique)#
Le point commun de ces méthodes est qu’elles ne sont pas supervisées. L’objectif est de réduire la complexité des données. Réduire le nombre de dimensions pour l’ACP ou segmenter les observations pour les k-means et la CAH. On propose d’utiliser une CAH sur les mêmes données.
Le module scikit-learn.cluster ne propose pas de fonction pour dessiner le dendrogram. Il faudra utiliser celle-ci : dendrogram et sans doute s’inspirer du code suivant.
from sklearn.cluster import AgglomerativeClustering
from scipy.cluster.hierarchy import dendrogram
ward = AgglomerativeClustering(linkage='ward', compute_full_tree=True).fit(df)
dendro = [ ]
for a,b in ward.children_:
dendro.append([a, b, float(len(dendro)+1), len(dendro)+1])
fig = plt.figure(figsize=(8, 8))
ax = fig.add_subplot(1, 1, 1)
r = dendrogram(dendro, color_threshold=1, labels=list(df.index),
show_leaf_counts=True, ax=ax, orientation="left")

Exercice 2 : régression#
Ce sont trois méthodes supervisées : on s’en sert pour expliquer prédire
le lien entre deux variables et
(ou ensemble de
variables) ou prédire
en fonction de
. Pour cet
exercice, on récupère des données relatives aux salaires Salaires et
revenus
d’activités
(les chercher avec la requête insee données dads sur un moteur de
recherche). La récupération des données est assez fastidieuse. La
première étape consiste à télécharger les données depuis le site de
l’INSEE. La seconde étape consiste à
convertir les données au format
sqlite3. Pour ce
fichier, ce travail a déjà été effectué et peut être téléchargé depuis
mon site. La base comprend 2 millions de lignes.
import pyensae.datasource
f = pyensae.datasource.download_data("dads2011_gf_salaries11_dbase.zip",
website="https://www.insee.fr/fr/statistiques/fichier/2011542/")
f
['.\salaries11.dbf', 'varlist_salaries11.dbf', '.\varmod_salaries11.dbf']
import pandas
try:
from dbfread import DBF
use_dbfread = True
except ImportError as e :
use_dbfread = False
if use_dbfread:
import os
from pyensae.sql.database_exception import ExceptionSQL
from pyensae.datasource import dBase2sqllite
print("convert dbase into sqllite")
try:
dBase2sqllite("salaries2011.db3", "varlist_salaries11.dbf", overwrite_table="varlist")
dBase2sqllite("salaries2011.db3", "varmod_salaries11.dbf", overwrite_table="varmod")
dBase2sqllite("salaries2011.db3", 'salaries11.dbf',
overwrite_table="salaries", fLOG = print)
except ExceptionSQL:
print("La base de données est déjà renseignée.")
else :
print("use of zipped version")
import pyensae.datasource
db3 = pyensae.datasource.download_data("salaries2011.zip")
# pour aller plus vite, données à télécharger au
# http://www.xavierdupre.fr/enseignement/complements/salaries2011.zip
convert dbase into sqllite
SQL 'drop table if exists salaries11'
SQL 'create table salaries (A6 TEXT, A17 TEXT, A38 TEXT, REGR TEXT, DEPR TEXT, REGT TEXT, DEPT TEXT, SEXE TEXT, PCS TEXT, CONT_TRAV TEXT, CONV_COLL TEXT, TYP_EMPLOI TEXT, DUREE REAL, DATDEB REAL, DATFIN REAL, CPFD TEXT, DOMEMPL TEXT, DOMEMPL_EM TEXT, FILT TEXT, AGE REAL, CS TEXT, NB_PER REAL, NB_PER_N REAL, NBHEUR REAL, NBHEUR_TOT REAL, TRALCHT TEXT, TREFF TEXT, TRNNETO TEXT, POND REAL)'
moving line 0 to table salaries
moving line 20000 to table salaries
moving line 40000 to table salaries
moving line 60000 to table salaries
moving line 80000 to table salaries
moving line 100000 to table salaries
moving line 120000 to table salaries
moving line 140000 to table salaries
moving line 160000 to table salaries
moving line 180000 to table salaries
moving line 200000 to table salaries
moving line 220000 to table salaries
moving line 240000 to table salaries
moving line 260000 to table salaries
moving line 280000 to table salaries
moving line 300000 to table salaries
moving line 320000 to table salaries
moving line 340000 to table salaries
moving line 360000 to table salaries
moving line 380000 to table salaries
moving line 400000 to table salaries
moving line 420000 to table salaries
moving line 440000 to table salaries
moving line 460000 to table salaries
moving line 480000 to table salaries
moving line 500000 to table salaries
moving line 520000 to table salaries
moving line 540000 to table salaries
moving line 560000 to table salaries
moving line 580000 to table salaries
moving line 600000 to table salaries
moving line 620000 to table salaries
moving line 640000 to table salaries
moving line 660000 to table salaries
moving line 680000 to table salaries
moving line 700000 to table salaries
moving line 720000 to table salaries
moving line 740000 to table salaries
moving line 760000 to table salaries
moving line 780000 to table salaries
moving line 800000 to table salaries
moving line 820000 to table salaries
moving line 840000 to table salaries
moving line 860000 to table salaries
moving line 880000 to table salaries
moving line 900000 to table salaries
moving line 920000 to table salaries
moving line 940000 to table salaries
moving line 960000 to table salaries
moving line 980000 to table salaries
moving line 1000000 to table salaries
moving line 1020000 to table salaries
moving line 1040000 to table salaries
moving line 1060000 to table salaries
moving line 1080000 to table salaries
moving line 1100000 to table salaries
moving line 1120000 to table salaries
moving line 1140000 to table salaries
moving line 1160000 to table salaries
moving line 1180000 to table salaries
moving line 1200000 to table salaries
moving line 1220000 to table salaries
moving line 1240000 to table salaries
moving line 1260000 to table salaries
moving line 1280000 to table salaries
moving line 1300000 to table salaries
moving line 1320000 to table salaries
moving line 1340000 to table salaries
moving line 1360000 to table salaries
moving line 1380000 to table salaries
moving line 1400000 to table salaries
moving line 1420000 to table salaries
moving line 1440000 to table salaries
moving line 1460000 to table salaries
moving line 1480000 to table salaries
moving line 1500000 to table salaries
moving line 1520000 to table salaries
moving line 1540000 to table salaries
moving line 1560000 to table salaries
moving line 1580000 to table salaries
moving line 1600000 to table salaries
moving line 1620000 to table salaries
moving line 1640000 to table salaries
moving line 1660000 to table salaries
moving line 1680000 to table salaries
moving line 1700000 to table salaries
moving line 1720000 to table salaries
moving line 1740000 to table salaries
moving line 1760000 to table salaries
moving line 1780000 to table salaries
moving line 1800000 to table salaries
moving line 1820000 to table salaries
moving line 1840000 to table salaries
moving line 1860000 to table salaries
moving line 1880000 to table salaries
moving line 1900000 to table salaries
moving line 1920000 to table salaries
moving line 1940000 to table salaries
moving line 1960000 to table salaries
moving line 1980000 to table salaries
moving line 2000000 to table salaries
moving line 2020000 to table salaries
moving line 2040000 to table salaries
moving line 2060000 to table salaries
moving line 2080000 to table salaries
moving line 2100000 to table salaries
moving line 2120000 to table salaries
moving line 2140000 to table salaries
moving line 2160000 to table salaries
moving line 2180000 to table salaries
moving line 2200000 to table salaries
moving line 2220000 to table salaries
moving line 2240000 to table salaries
Les données des salaires ne sont pas numériques, elles correspondent à des intervalles qu’on convertit en prenant le milieu de l’intervalle. Pour le dernier, on prend la borne supérieure.
import sqlite3, pandas
con = sqlite3.connect("salaries2011.db3")
df = pandas.io.sql.read_sql("select * from varmod", con)
con.close()
values = df[ df.VARIABLE == "TRNNETO"].copy()
def process_intervalle(s):
# [14 000 ; 16 000[ euros
acc = "0123456789;+"
s0 = "".join(c for c in s if c in acc)
spl = s0.split(';')
if len(spl) != 2:
raise ValueError("Unable to process '{0}'".format(s0))
try:
a = float(spl[0])
except Exception as e:
raise ValueError("Cannot interpret '{0}' - {1}".format(s, spl))
b = float(spl[1]) if "+" not in spl[1] else None
if b is None:
return a
else:
return (a+b) / 2.0
values["montant"] = values.apply(lambda r : process_intervalle(r ["MODLIBELLE"]), axis = 1)
values.head()
| VARIABLE | MODALITE | MODLIBELLE | montant | |
|---|---|---|---|---|
| 8957 | TRNNETO | 00 | [0 ; 200[ euros | 100.0 |
| 8958 | TRNNETO | 01 | [200 ; 500[ euros | 350.0 |
| 8959 | TRNNETO | 02 | [500 ; 1 000[ euros | 750.0 |
| 8960 | TRNNETO | 03 | [1 000 ; 1 500[ euros | 1250.0 |
| 8961 | TRNNETO | 04 | [1 500 ; 2 000[ euros | 1750.0 |
On crée la base d’apprentissage :
import sqlite3, pandas
con = sqlite3.connect("salaries2011.db3")
data = pandas.io.sql.read_sql("select TRNNETO,AGE,SEXE from salaries", con)
con.close()
salaires = data.merge ( values, left_on="TRNNETO", right_on="MODALITE" )
salaires.head()
| TRNNETO | AGE | SEXE | VARIABLE | MODALITE | MODLIBELLE | montant | |
|---|---|---|---|---|---|---|---|
| 0 | 02 | 49.0 | 1 | TRNNETO | 02 | [500 ; 1 000[ euros | 750.0 |
| 1 | 02 | 27.0 | 1 | TRNNETO | 02 | [500 ; 1 000[ euros | 750.0 |
| 2 | 02 | 22.0 | 1 | TRNNETO | 02 | [500 ; 1 000[ euros | 750.0 |
| 3 | 02 | 26.0 | 1 | TRNNETO | 02 | [500 ; 1 000[ euros | 750.0 |
| 4 | 02 | 29.0 | 2 | TRNNETO | 02 | [500 ; 1 000[ euros | 750.0 |
On récupère les variables utiles pour la régression.
salaires["M"] = salaires.apply( lambda r : 1 if r["SEXE"] == "1" else 0, axis=1)
salaires["F"] = 1 - salaires["M"] # en supposant que le sexe est toujours renseigné
data = salaires[["AGE", "M", "F", "montant"]]
data = data[data.M + data.F > 0]
data.head()
| AGE | M | F | montant | |
|---|---|---|---|---|
| 0 | 49.0 | 1 | 0 | 750.0 |
| 1 | 27.0 | 1 | 0 | 750.0 |
| 2 | 22.0 | 1 | 0 | 750.0 |
| 3 | 26.0 | 1 | 0 | 750.0 |
| 4 | 29.0 | 0 | 1 | 750.0 |
Ce type d’écriture est plutôt lent car une fonction Python est exécutée à chaque itération. Il est préférable dès que c’est possible d’utiliser les expressions avec des indices sans passer par la fonction apply qui créé une copie de chaque ligne avant d’appliquer la fonction à appliquer à chacune d’entre elles.
salaires["M2"] = 0
salaires.loc[salaires["SEXE"] == "1", "M2"] = 1
salaires["F2"] = 1 - salaires["M2"]
salaires.head()
| TRNNETO | AGE | SEXE | VARIABLE | MODALITE | MODLIBELLE | montant | M | F | M2 | F2 | |
|---|---|---|---|---|---|---|---|---|---|---|---|
| 0 | 02 | 49.0 | 1 | TRNNETO | 02 | [500 ; 1 000[ euros | 750.0 | 1 | 0 | 1 | 0 |
| 1 | 02 | 27.0 | 1 | TRNNETO | 02 | [500 ; 1 000[ euros | 750.0 | 1 | 0 | 1 | 0 |
| 2 | 02 | 22.0 | 1 | TRNNETO | 02 | [500 ; 1 000[ euros | 750.0 | 1 | 0 | 1 | 0 |
| 3 | 02 | 26.0 | 1 | TRNNETO | 02 | [500 ; 1 000[ euros | 750.0 | 1 | 0 | 1 | 0 |
| 4 | 02 | 29.0 | 2 | TRNNETO | 02 | [500 ; 1 000[ euros | 750.0 | 0 | 1 | 0 | 1 |
Il ne reste plus qu’à faire la régression.
version scikit-learn#
Vous pouvez vous inspirer de cet exemple.
version statsmodels#
L’exemple avec ce module est ici.