KMeans with norm L1

Links: notebook, html, PDF, python, slides, GitHub

This demonstrates how results change when using norm L1 for a k-means algorithm.

from jyquickhelper import add_notebook_menu
add_notebook_menu()

%matplotlib inline

import matplotlib.pyplot as plt

Simple datasets

import numpy
import numpy.random as rnd
N = 1000
X = numpy.zeros((N * 2, 2), dtype=numpy.float64)
X[:N] = rnd.rand(N, 2)
X[N:] = rnd.rand(N, 2)
#X[N:, 0] += 0.75
X[N:, 1] += 1
X[:N//10, 0] -= 2
X.shape

(2000, 2)

fig, ax = plt.subplots(1, 1)
ax.plot(X[:, 0], X[:, 1], '.')
ax.set_title("Two squares");

Classic KMeans

It uses euclidean distance.

from sklearn.cluster import KMeans
km = KMeans(2)
km.fit(X)

KMeans(n_clusters=2)

km.cluster_centers_

array([[0.27360385, 0.50114694],
       [0.49920054, 1.50108811]])

def plot_clusters(km_, X, ax):
    lab = km_.predict(X)
    for i in range(km_.cluster_centers_.shape[0]):
        sub = X[lab == i]
        ax.plot(sub[:, 0], sub[:, 1], '.', label='c=%d' % i)
    C = km_.cluster_centers_
    ax.plot(C[:, 0], C[:, 1], 'o', ms=15, label="centers")
    ax.legend()

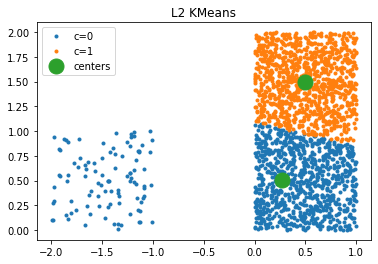
fig, ax = plt.subplots(1, 1)
plot_clusters(km, X, ax)
ax.set_title("L2 KMeans");

KMeans with L1 norm

from mlinsights.mlmodel import KMeansL1L2
kml1 = KMeansL1L2(2, norm='L1')
kml1.fit(X)

KMeansL1L2(n_clusters=2, norm='l1')

kml1.cluster_centers_

array([[0.5812874 , 1.49145705],
       [0.33319472, 0.4959633 ]])

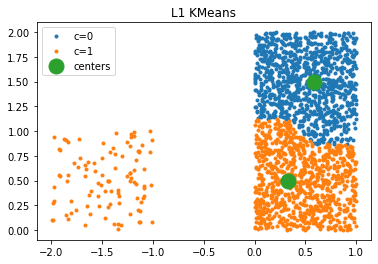
fig, ax = plt.subplots(1, 1)
plot_clusters(kml1, X, ax)
ax.set_title("L1 KMeans");

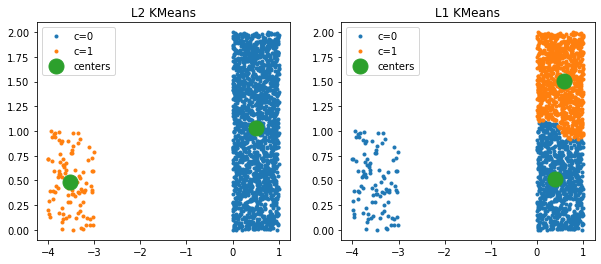
When clusters are completely different

N = 1000
X = numpy.zeros((N * 2, 2), dtype=numpy.float64)
X[:N] = rnd.rand(N, 2)
X[N:] = rnd.rand(N, 2)
#X[N:, 0] += 0.75
X[N:, 1] += 1
X[:N//10, 0] -= 4
X.shape

(2000, 2)

km = KMeans(2)
km.fit(X)

KMeans(n_clusters=2)

kml1 = KMeansL1L2(2, norm='L1')
kml1.fit(X)

KMeansL1L2(n_clusters=2, norm='l1')

fig, ax = plt.subplots(1, 2, figsize=(10, 4))
plot_clusters(km, X, ax[0])
plot_clusters(kml1, X, ax[1])
ax[0].set_title("L2 KMeans")
ax[1].set_title("L1 KMeans");